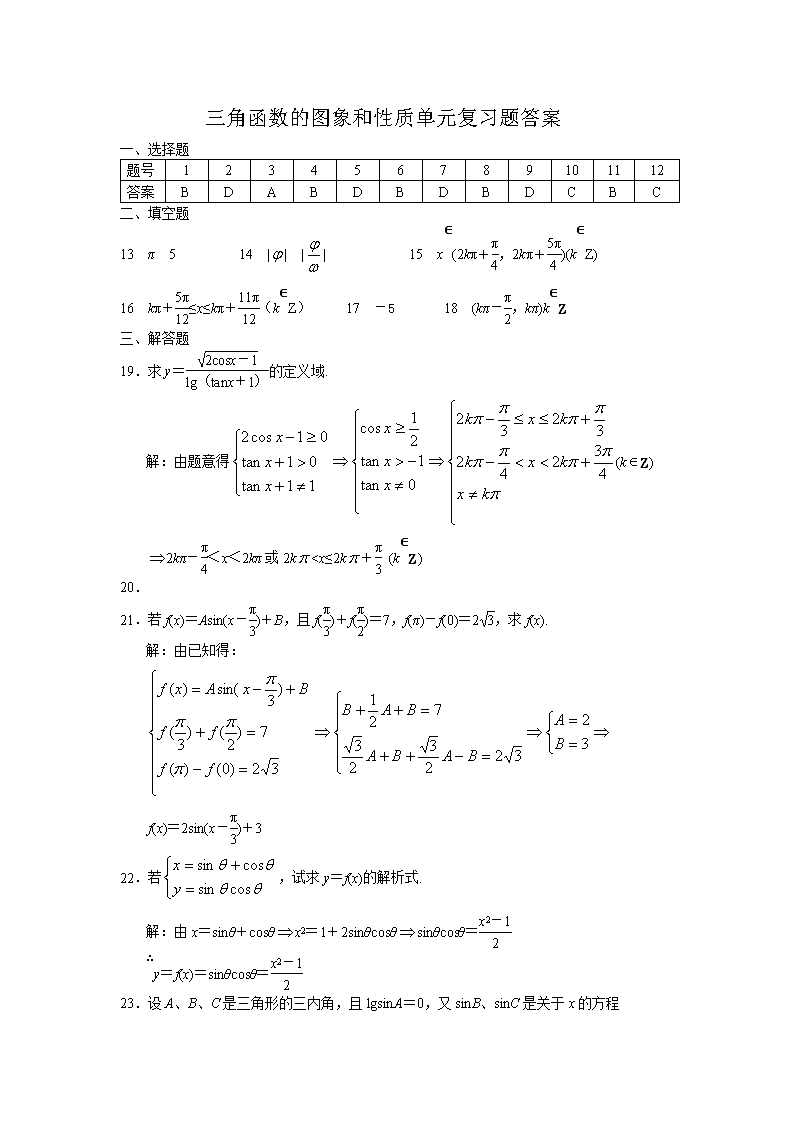高一数学专题练习：三角函数的图象和性质单元练习题 14页

三角函数的图象和性质单元练习题 ‎1．函数y＝tanx是 A.周期为π的偶函数 B.周期为π的奇函数C.周期为π的偶函数 D.周期为π的奇函数 ‎ ‎2．已知f(x)＝sin(x＋),g(x)＝cos(x－），则f(x)的图象 A.与g(x)的图象相同 B.与g(x)的图象关于y轴对称 C.向左平移个单位，得到g(x)的图象 D.向右平移个单位，得到g(x)的图象 ‎ ‎3．若x∈(0，2π)，函数y＝＋的定义域是 A.( ,π］ B.( ,π) C.(0,π) D.( ,2π) ‎ ‎4．函数y＝sin(2x＋)的图象的一条对称轴方程为 A.x＝ B.x＝－ C.x＝ D.x＝ ‎5．函数y＝logcos1cosx的值域是 A.［－1，1］ B.(－∞，＋∞) C. D.［0，＋∞)‎ ‎6．如果｜x｜≤，那么函数f(x)＝cos2x＋sinx的最小值是 A. B. C.－ D.－1‎ ‎7．函数f(x)＝sin，g(x)＝cos，则 A.f(x)与g(x)皆为奇函数 B.f(x)与g(x)皆为偶函数 C.f(x)是奇函数，g(x)是偶函数 D.f(x)是偶函数，g(x)是奇函数 ‎8．下列函数中，图象关于原点对称的是 A.y＝－｜sinx｜ B.y＝－x·sin｜x｜ C.y＝sin(－｜x｜) D.y＝sin｜x｜‎ ‎9．要得到函数y＝sin(2x－)的图象，只要将y＝sin2x的图象 A.向左平移 B.向右平移 C.向左平移 D.向右平移 ‎ ‎10．下图是函数y＝2sin(ωx＋)(||＜）的图象，那么 A.ω＝，＝ B.ω＝，＝－ C.ω＝2，＝D.ω＝2，＝－ ‎11．在［0，2π］上满足sinx≥的x的取值范围是 A.［0，］ B.［，］ C.［，］ D.［，π］ ‎ ‎12．函数y＝5＋sin22x的最小正周期为 A.2π B.π C. D. ‎ 二、填空题（4×6＝24分）‎ ‎13．若函数y＝Acos(ωx－3)的周期为2，则ω＝ ；若最大值是5，则A＝ .‎ ‎14．由y＝sinωx变为y＝Asin(ωx＋)，若“先平移，后伸缩”，则应平移 个单位；若“先伸缩，后平移”，则应平移 个单位即得y＝sin(ωx＋)；再把纵坐标扩大到原来的A倍，就是y＝Asin(ωx＋)(其中A＞0).‎ ‎15．不等式sinx＞cosx的解集为 . ‎ ‎16．函数y＝sin(－2x＋)的递增区间是 . ‎ ‎17．已知f(x)＝ax＋bsin3x＋1(a，b为常数)，且f (5)＝7，则f (－5)＝ . ‎ ‎18．使函数y＝2tanx与y＝cosx同时为单调递增的区间是 .‎ ‎19．求y＝的定义域.‎ ‎20．若f(x)＝Asin(x－)＋B，且f()＋f()＝7，f(π)－f(0)＝2，求f(x).‎ ‎21．若，试求y＝f(x)的解析式.‎ ‎23．设A、B、C是三角形的三内角，且lgsinA＝0，又sinB、sinC是关于x的方程 ‎4x2－2(＋1)x＋k＝0的两个根，求实数k的值.‎ ‎ 三角函数的图象和性质单元复习题答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D A B D B D B D C B C 二、填空题 ‎13 π 5 14 || || 15 x∈(2kπ＋，2kπ＋)(k∈Z) ‎ ‎16 kπ＋≤x≤kπ＋（k∈Z） 17 －5 18 (kπ－，kπ)k∈Z ‎ 三、解答题 ‎19．求y＝的定义域.‎ 解：由题意得(kZ)‎ ‎2kπ－＜x＜2kπ或2k0时， ；‎ ‎ （2）当a<0时，‎ ‎．‎ ‎21．（1）；‎ ‎ （2）．‎ ‎22．定义域：‎ ‎ 最小正周期：π 当时递增 ‎ 当时 ‎ y没有最大值.‎ 三角函数的图象和性质单元练习题 一、选择题（5×12＝60分）‎ ‎1．函数y＝tanx是 A.周期为π的偶函数 B.周期为π的奇函数 C.周期为π的偶函数 D.周期为π的奇函数 ‎ ‎2．已知f(x)＝sin(x＋),g(x)＝cos(x－），则f(x)的图象 A.与g(x)的图象相同 B.与g(x)的图象关于y轴对称 C.向左平移个单位，得到g(x)的图象 D.向右平移个单位，得到g(x)的图象 ‎ ‎3．若x∈(0，2π)，函数y＝＋的定义域是 A.( ,π］ B.( ,π) C.(0,π) D.( ,2π) ‎ ‎4．函数y＝sin(2x＋)的图象的一条对称轴方程为 A.x＝ B.x＝－ C.x＝ D.x＝ ‎5．函数y＝logcos1cosx的值域是 A.［－1，1］ B.(－∞，＋∞) C. D.［0，＋∞)‎ ‎6．如果｜x｜≤，那么函数f(x)＝cos2x＋sinx的最小值是 A. B. C.－ D.－1‎ ‎7．函数f(x)＝sin，g(x)＝cos，则 A.f(x)与g(x)皆为奇函数 B.f(x)与g(x)皆为偶函数 C.f(x)是奇函数，g(x)是偶函数 D.f(x)是偶函数，g(x)是奇函数 ‎8．下列函数中，图象关于原点对称的是 A.y＝－｜sinx｜ B.y＝－x·sin｜x｜‎ C.y＝sin(－｜x｜) D.y＝sin｜x｜‎ ‎9．要得到函数y＝sin(2x－)的图象，只要将y＝sin2x的图象 A.向左平移 B.向右平移 C.向左平移 D.向右平移 ‎ ‎10．下图是函数y＝2sin(ωx＋)(||＜）的图象，那么 A.ω＝，＝ B.ω＝，＝－ C.ω＝2，＝ D.ω＝2，＝－ ‎11．在［0，2π］上满足sinx≥的x的取值范围是 A.［0，］ B.［，］ C.［，］ D.［，π］ ‎ ‎12．函数y＝5＋sin22x的最小正周期为 A.2π B.π C. D. ‎ 二、填空题（4×6＝24分）‎ ‎13．若函数y＝Acos(ωx－3)的周期为2，则ω＝ ；若最大值是5，则A＝ .‎ ‎14．由y＝sinωx变为y＝Asin(ωx＋)，若“先平移，后伸缩”，则应平移 个单位；若“先伸缩，后平移”，则应平移 个单位即得y＝sin(ωx＋)；再把纵坐标扩大到原来的A倍，就是y＝Asin(ωx＋)(其中A＞0).‎ ‎15．不等式sinx＞cosx的解集为 . ‎ ‎16．函数y＝sin(－2x＋)的递增区间是 . ‎ ‎17．已知f(x)＝ax＋bsin3x＋1(a，b为常数)，且f (5)＝7，则f (－5)＝ . ‎ ‎18．使函数y＝2tanx与y＝cosx同时为单调递增的区间是 .‎ 第Ⅱ卷 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二、填空题 ‎13 14 15 ‎ ‎16 17 18 ‎ 三、解答题 ‎19．求y＝的定义域.‎ ‎20．已知：＝3，‎ 求：的值. ‎ ‎21．若f(x)＝Asin(x－)＋B，且f()＋f()＝7，f(π)－f(0)＝2，求f(x).‎ ‎22．若，试求y＝f(x)的解析式.‎ ‎23．设A、B、C是三角形的三内角，且lgsinA＝0，又sinB、sinC是关于x的方程 ‎4x2－2(＋1)x＋k＝0的两个根，求实数k的值.‎ 三角函数的图象和性质单元复习题答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D A B D B D B D C B C 二、填空题 ‎13 π 5 14 || || 15 x∈(2kπ＋，2kπ＋)(k∈Z) ‎ ‎16 kπ＋≤x≤kπ＋（k∈Z） 17 －5 18 (kπ－，kπ)k∈Z ‎ 三、解答题 ‎19．求y＝的定义域.‎ 解：由题意得(kZ)‎ ‎2kπ－＜x＜2kπ或2k