高考理科数学复习练习作业85 9页

题组层级快练(八十五)‎ ‎1．(2017·甘肃河西五市联考)设随机变量ξ服从正态分布N(0，1)，若P(ξ>2)＝p，即P(－2<ξ<0)＝(　　)‎ A.＋p　　　　　　　　 B．1－p C.－p D．1－2p 答案　C 解析　由对称性知P(ξ≤－2)＝p，所以P(－2<ξ<0)＝＝－p.‎ ‎2．(2017·广东佛山一模)已知随机变量X服从正态分布N(3，1)，且P(2≤ξ≤4)＝0.682 6，则P(ξ>4)＝(　　)‎ A．0.158 8 B．0.158 7‎ C．0.158 6 D．0.158 5‎ 答案　B 解析　由正态曲线性质知，其图像关于直线x＝3对称，‎ ‎∴P(ξ>4)＝＝0.5－×0.682 6＝0.158 7，故选B.‎ ‎3．已知随机变量ξ服从正态分布N(0，σ2)，P(ξ>2)＝0.023，则P(－2≤ξ≤2)＝(　　)‎ A．0.954 B．0.977‎ C．0.488 D．0.477‎ 答案　A 解析　P(－2≤ξ≤2)＝1－2P(ξ>2)＝0.954.‎ ‎4．(2017·南昌调研)某单位1 000名青年职员的体重x(单位：kg)服从正态分布N(μ，22)，且正态分布的密度曲线如图所示，若体重在58.5～62.5 kg属于正常，则这1 000名青年职员中体重属于正常的人数约是(　　)‎ A．683 B．841‎ C．341 D．667‎ 答案　A 解析　∵P(58.50)，若ξ在(80，120)内的概率为0.8，则落在(0，80)内的概率为(　　)‎ A．0.05 B．0.1‎ C．0.15 D．0.2‎ 答案　B 解析　∵ξ服从正态分布N(100，σ2)，∴曲线的对称轴是直线μ＝100，∵ξ在(80，120)内取值的概率为0.8，ξ在(0，100)内取值的概率为0.5，‎ ‎∴ξ在(0，80)内取值的概率为0.5－0.4＝0.1.故选B.‎ ‎6．(2017·河南安阳专项训练)已知某次数学考试的成绩服从正态分布N(116，64)，则成绩在140分以上的考生所占的百分比为(　　)‎ A．0.3% B．0.23%‎ C．1.5% D．0.15%‎ 答案　D 解析　依题意，得μ＝116，σ＝8，所以μ－3σ＝92，μ＋3σ＝140.而服从正态分布的随机变量在(μ－3σ，μ＋3σ)内取值的概率约为0.997，所以成绩在区间(92，140)内的考生所占的百分比约为99.7%.从而成绩在140分以上的考生所占的百分比为＝0.15%.故选D.‎ ‎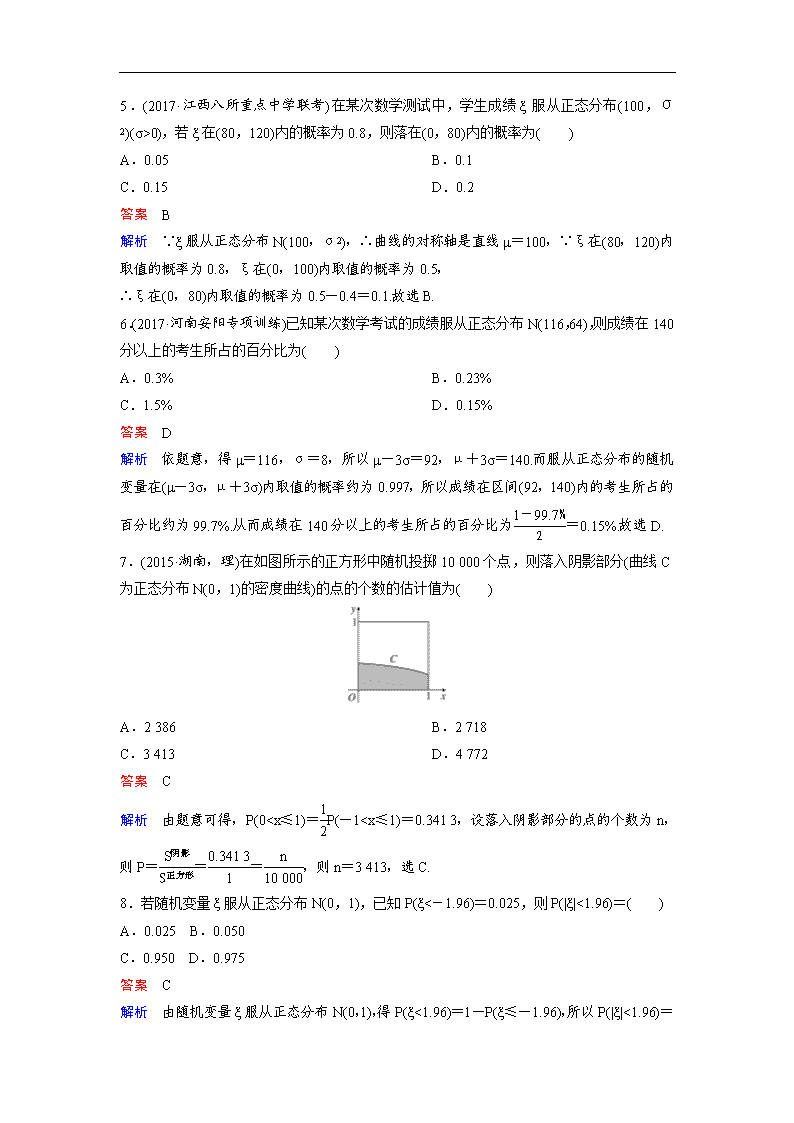7．(2015·湖南，理)在如图所示的正方形中随机投掷10 000个点，则落入阴影部分(曲线C为正态分布N(0，1)的密度曲线)的点的个数的估计值为(　　)‎ A．2 386 B．2 718‎ C．3 413 D．4 772‎ 答案　C 解析　由题意可得，P(0P2 B．P11)＝a，a为常数，则P(－1≤ξ≤0)＝________．‎ 答案　－a 解析　由正态曲线的对称轴为ξ＝0，又P(ξ>1)＝a，故P(ξ<－1)＝a.所以P(－1≤ξ≤0)＝＝－a，即答案为－a.‎ ‎8．(2017·沧州七校联考)2015年中国汽车销售量达到1 700万辆，汽车耗油量对汽车的销售有着非常重要的影响，各个汽车制造企业积极采用新技术降低耗油量，某汽车制造公司为调查某种型号的汽车的耗油情况，共抽查了1 200名车主，据统计该种型号的汽车的平均耗油为百公里8.0升，并且汽车的耗油量ξ服从正态分布N(8，σ2)，已知耗油量ξ∈[7，9]的概率为0.7，那么耗油量大于9升的汽车大约有________辆．‎ 答案　180‎ 思路　首先根据题意确定正态分布的对称轴，利用正态曲线的对称性即可求得ξ>9的概率，利用概率来估计样本中满足条件的汽车数量．‎ 解析　由题意可知ξ～N(8，σ2)，故正态分布曲线以μ＝8为对称轴．又因为P(7≤ξ≤9)＝0.7，故P(7≤ξ≤9)＝2P(8≤ξ≤9)＝0.7，所以P(8≤ξ≤9)＝0.35.而P(ξ≥8)＝0.5，所以P(ξ>9)＝0.15.故耗油量大于9升的汽车大约有1 200×0.15＝180辆．‎ ‎9．若一个正态分布的概率密度函数是一个偶函数，且该函数的最大值为.‎ ‎(1)求该正态分布的概率密度函数的解析式；‎ ‎(2)求正态总体在(－4，4]内的概率．‎ 答案　(1)φμ，σ(x)＝e－，x∈(－∞，＋∞)‎ ‎(2)0.682 6‎ 解析　(1)由于该正态分布的概率密度函数是一个偶函数，所以其图像关于y轴对称，即μ＝0.由＝，得σ＝4.故该正态分布的概率密度函数的解析式是φμ，σ(x)＝e－，x∈(－∞，＋∞)．‎ ‎(2)P(－4＜ξ≤4)＝P(0－4＜ξ≤0＋4)＝P(μ－σ＜ξ≤μ＋σ)＝0.682 6.‎ ‎10．已知某种零件的尺寸ξ(单位：mm)服从正态分布，其正态曲线在(0，80)上是增函数，在(80，＋∞)上是减函数，且f(80)＝.‎ ‎(1)求概率密度函数；‎ ‎(2)估计尺寸在72 mm～88 mm间的零件大约占总数的百分之几？‎ 答案　(1)φμ，σ(x)＝e－　(2)68.26%‎ 解析　(1)由于正态曲线在(0，80)上是增函数，在(80，＋∞)上是减函数，‎ 所以正态曲线关于直线x＝80对称，且在x＝80处取得最大值．‎ 因此得μ＝80，＝，所以σ＝8.‎ 故密度函数解析式是φμ，σ(x)＝e－.‎ ‎(2)由μ＝80，σ＝8，得μ－σ＝80－8＝72，μ＋σ＝80＋8＝88.‎ 所以零件尺寸ξ位于区间(72，88)内的概率是0.682 6.‎ 因此尺寸在72 mm～88 mm间的零件大约占总数的68.26%.‎