上海教育高中数学一年级上册期末测试题一 7页

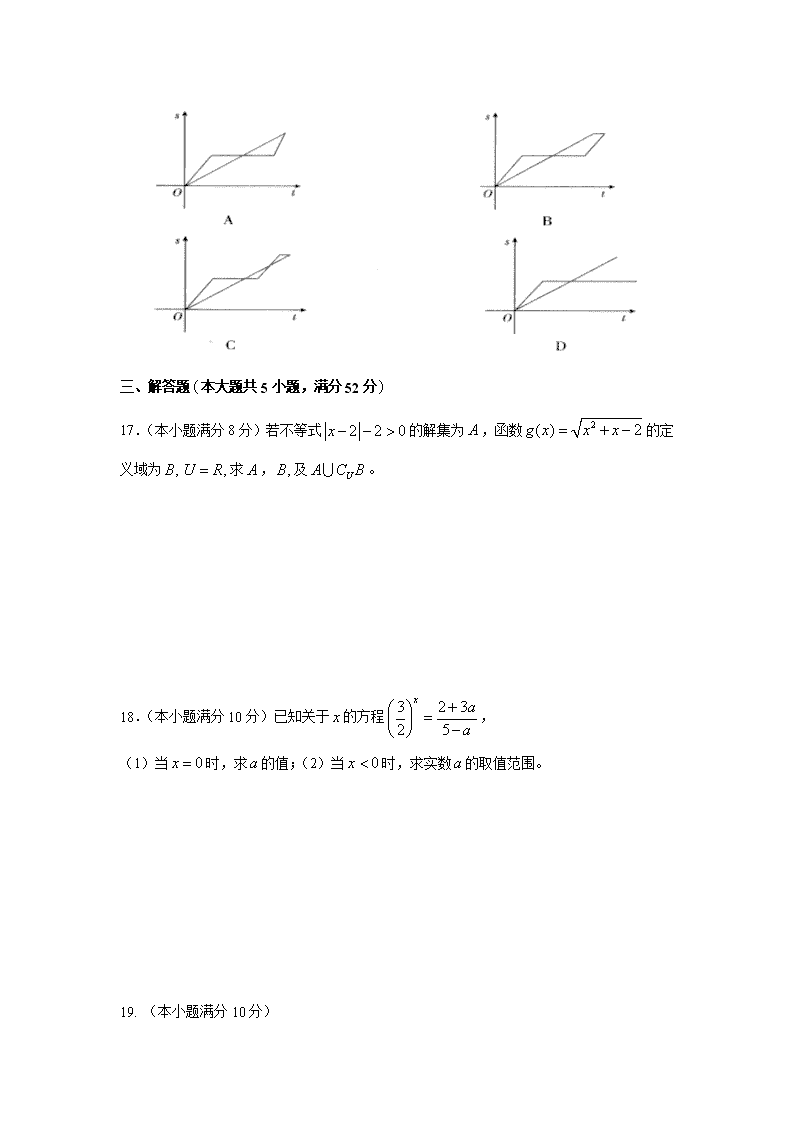
上海市浦东新区2009学年度第一学期期末质量抽测 高 一 数 学 试 卷 ‎（完卷时间：90分钟 满分：100分） 2010年1月 题 号 一 二 三 总 分 ‎1-12‎ ‎13-16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ 得 分 一、填空题 本大题共12小题，每小题3分，满分36分 ‎1．设，则集合= ．‎ ‎2．命题“在整数集中，若都是偶数，则是偶数”的否命题是：‎ ‎ ．‎ ‎3．已知实数满足，，则与的大小关系是_____．‎ ‎4．与函数的图像关于轴对称的函数解析式是 ．‎ ‎5．已知，则的最大值是_______． ‎ ‎6．已知函数，若，则的值域是 ．‎ ‎7．设函数=，则 ________．‎ ‎8．已知函数，且，则实数的取值范围是____________．‎ ‎9．已知奇函数在区间上的解析式为，则在区间上的解析式＝ ．‎ ‎10．试写出满足“对定义域内任意实数，都有”的函数的一个实例：___________________．‎ ‎11. 已知函数的图象是连续不断的，有如下的对应值表.‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ y ‎－5‎ ‎2‎ ‎8‎ ‎12‎ ‎－5‎ ‎－10‎ ‎ 则函数上的零点至少有_______个．‎ ‎12．如图是某池塘中野生水葫芦的面积与时间的函数关系图像。假设其函数关系为指数函数，并给出下列说法：‎ ‎①此指数函数的底数为2；‎ ‎②在第5个月时，野生水葫芦的面积会超过30；‎ ‎③野生水葫芦从4蔓延到12只需1.5个月；‎ ‎④设野生水葫芦蔓延至2、3、6所需的 时间分别为、、，则有；‎ 其中正确的说法有 . (请把正确的说法的序号都填在横线上).‎ 二、选择题 本大题共4小题，每小题3分，满分12分 ‎13．“”是“函数在区间上为增函数”的 ---------------（ ）‎ ‎ （A）充分非必要条件 （B）必要非充分条件 ‎（C）充要条件 （D）既非充分又非必要条件 ‎14．已知实数，且，则下列结论中一定成立的是 --------------（ ）‎ ‎ （A） （B） （C） （D）‎ ‎15．为了得到函数的图象，可以把函数的图象适当平移，这个平移 ‎（A）沿轴向右平移个单位 （B）沿轴向右平移个单位 ‎（C）沿轴向左平移个单位 （D）沿轴向左平移个单位 ‎16．“龟兔赛跑”讲述了这样的故事：同时起跑后，领先的兔子看着慢慢爬行的乌龟，骄傲起来，睡了一觉，当它醒来时，发现乌龟快到终点了，于是急忙追赶，但为时已晚，乌龟还是先到达了终点……，下列图形表示的是乌龟和兔子所行的路程与时间的函数图象，则与故事情节相吻合的是 ---------------（ ）‎ 三、解答题本大题共5小题，满分52分 ‎17．（本小题满分8分）若不等式的解集为，函数的定义域为求，及。‎ ‎18．（本小题满分10分）已知关于的方程，‎ ‎（1）当时，求的值；（2）当时，求实数的取值范围。‎ ‎19. （本小题满分10分）‎ 已知关于x的二次方程有实数根，且两根分别为、，（1）求证：++的值为定值，并写出这个定值；‎ ‎（2）求的最大值.‎ ‎20. （本小题满分10分）‎ 如图设计一幅矩形宣传画，要求画面面积为‎4840 cm2，画面上下边要留‎8cm空白，左右要留‎5cm空白，怎样确定画面的高与宽的尺寸，才能使宣传画面所用纸张面积最小？‎ ‎5‎ ‎8‎ ‎ ‎ ‎21. （本小题满分12分）已知函数.‎ ‎ （1）的值为多少时，是偶函数？‎ ‎ （2）若对任意，都有，求实数的取值范围．‎ ‎ （3）若在区间上单调递增，求实数的取值范围．‎ 浦东新区2008学年度高一数学第一学期期末质量抽测评分标准 一、填空题 （本大题满分36分）‎ ‎1. ； 2. 在整数集中，若不都是偶数，则不是偶数； ‎ ‎3. ； 4. ； 5. ； 6. ； ‎ ‎7. ； 8. ； 9. 10. 等 ‎ ‎11. 2； 12. ①②④。‎ 二、选择题 （本大题满分12分）‎ ‎13.； 14. ； 15. ； 16．。 ‎ 三、解答题 （本大题满分52分）本大题共有5题，解答下列各题必须写出必要的步骤。‎ ‎17. （本题满分8分）‎ 解： --------2分 ‎ --------2分 ‎ --------2分 ‎ --------2分 ‎18. （本题满分10分）‎ ‎ 解：（1）当时， --------2分 ‎ 解得. --------2分 ‎（2）当时， --------2分 ‎ 即 解得. --------4分 ‎19. （本题满分10分） ‎ 解：(1)由韦达定理知 --------2分 为定值 --------1分 ‎(2) --------1分 又 --------2分 在上单调递增，时最大值为2， ---2分 在上单调递减，时最大值为-54，‎ 的最大值为2 --------2分 ‎ ‎20. （本题满分12分）‎ 解：设画面高为cm，宽为cm，依意有， --------2分 则所需纸张面积， ‎ ‎ 即, --------4分 ‎ ‎ ‎ -----------2分 ‎ 当且仅当，即时等号成立。 -----------2分 ‎ 即当画面高为‎88cm，宽为‎55cm时，所需纸张面积最小为‎6760cm2 - -------2分 ‎21. （本题满分12分 解：（1） -----------1分 又，，解得 -----------2分 ‎（2），，即 -----------1分 ‎ -----------1分 时，， ，. ----------2分 ‎（3）任取，则 -----------1分 即 ‎ ‎ -----------1分 ‎ -----------1分 而 -----------1分 ‎ -----------1分