2020_2021学年新教材高中数学第四章指数函数与对数函数4 42页

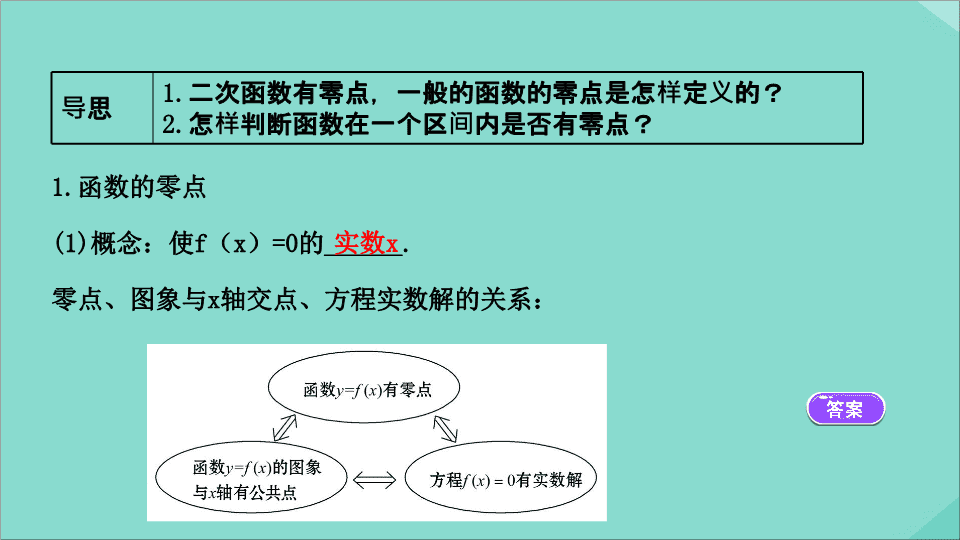
4.5 　函数的应用 ( 二 ) 4.5.1 　函数的零点与方程的解 必备知识 · 自主学习 1. 函数的零点 (1) 概念：使 f （ x ） =0 的 ______. 零点、图象与 x 轴交点、方程实数解的关系： 导思 1. 二次函数有零点，一般的函数的零点是怎样定义的？ 2. 怎样判断函数在一个区间内是否有零点？ 实数 x (2) 本质：方程 f(x)=0 的根、函数 y=f(x) 的图象与 x 轴的公共点的横坐标 . (3) 应用：利用零点、图象与 x 轴的交点、方程实数解的关系，实现三种问题的相互转化 . 【 思考 】 函数的零点是点吗？ 提示： 不是，是使 f(x)=0 的实数 x ，是方程 f(x)=0 的根 . 2. 函数零点存在定理 (1) 条件：函数 y=f(x) 在区间 [a,b] 上的图象是一条连续不断的曲线，且有 _____________ ； (2) 结论：函数 y=f(x) 在区间 (a,b) 内 ___________ 零点，即 ________________ ， 使 f(c)=0 ，这个 c 也就是方程 f(x)=0 的解 . (3) 本质：利用函数的性质判断零点的存在性 . (4) 应用：判断零点的存在性、求参数的范围等 . f(a) f(b) <0 至少有一个 存在 c∈(a,b) 【 思考 】 函数 y=f(x) 在区间 (a,b) 上有零点，是不是一定有 f(a) f(b) <0 ？ 提示： 不一定，如 f (x) =x 2 在区间 (-1, 1) 上有零点 0 ，但是 f (-1) f (1) =1×1=1>0. 【 基础小测 】 1. 辨析记忆 ( 对的打“√”，错的打“ ×”) (1) 函数 y=f(x) 在区间 [a,b] 上的图象是一条连续不断的曲线，且有 f(a)f(b)<0 ，则函数在区间 (a,b) 内有唯一的零点 . ( 　　 ) (2) 若函数 y=f(x) 在区间 (a ， b) 上 f(a)·f(b)>0 ，则在区间 (a ， b) 内一定没有零点 . ( 　　 ) (3) 函数 f(x)=x 2 -x+1 有零点 . ( 　　 ) 提示： (1)×. 在区间 (a ， b) 内至少有一个零点 . (2)×. 如 f(x)=x 2 在区间 (-1, 1) 上有 f(-1)f(1) =1×1=1>0 但是在区间 (-1, 1) 上有零点 0. (3)×. 因为方程 x 2 -x+1=0 的 Δ=1-4=-3<0 无根，所以函数没有零点 . 2. 已知定义在 R 上的函数 f(x) 的图象是连续的，且其中的四组对应值如表，那么在下列区间中，函数 f(x) 不一定存在零点的是 ( 　　 ) A.(1 ， 2) B.[1 ， 3] C.[2 ， 5) D.(3 ， 5) x 1 2 3 5 f(x) 3 -1 2 0 【 解析 】 选 D. 由题表可知， f(1)=3 ， f(2)=-1 ， f(3)=2 ， f(5)=0. 由 f(1) • f(2)<0 ，可知函数 f(x) 在 (1 ， 2) 上一定有零点；则函数 f(x) 在 [1 ， 3] 上一定有零点； 由 f(2) • f(3)<0 ，可知函数 f(x) 在 (2 ， 3) 上一定有零点，则函数 f(x) 在 [2 ， 5) 上一定有零点； 由 f(3)>0 ， f(5)=0 ，可知 f(x) 在 (3 ， 5) 上不一定有零点 . 所以函数 f(x) 不一定存在零点的是 (3 ， 5). 3.( 教材二次开发：例题改编 ) 函数 f(x)=ln x-6 的零点是 _______.  【 解析 】 令 f (x) =ln x-6=0 ，则 ln x=6 ，解得 x=e 6 . 答案： e 6 关键能力 · 合作学习 类型一　零点的概念及求法 ( 数学运算 ) 【 题组训练 】 1. 函数 f(x)=x 2 -3x-4 的零点是 ( 　　 ) A.-1 ， 0 B.0 ， 4 C.1 ， -4 D.-1 ， 4 2.( 多选题 ) 已知函数 f(x)= 则 f(x) 的零点为 ( 　　 ) A.1 B.-2 C.2 D.3 3. 若函数 f(x)=ax+1-2a 的零点是 ，则 a=_______.  【 解析 】 1. 选 D. 根据题意，函数 f(x)=x 2 -3x-4 ， 若 f(x)=0 ，即 x 2 -3x-4=0 ，解得 x=-1 或 4 ， 即函数的零点为 -1 ， 4. 2. 选 AC. 当 x<2 时，由 e x-1 -1=0 ，解得 x=1 ； 当 x≥2 时，由 log 3 =0 ，得 =1 ， 即 x 2 -1=3 ，解得 x=2. 所以 f(x) 的零点为 1 ， 2. 3. 依题意得 f =0 ，即 a+1-2a=0 ，解得 a= . 答案： 【 解题策略 】 函数零点的求法 (1) 代数法：求方程 f(x)=0 的实数根 . (2) 几何法：对于不能用求根公式的方程 f(x)=0 ，可以将它与函数 y=f(x) 的图象联系起来 . 图象与 x 轴的交点的横坐标即为函数的零点 . 类型二　零点个数的判断 ( 数学运算、逻辑推理 ) 【 典例 】 1. 函数 f(x)=x 3 -x 的零点的个数是 ( 　　 ) A.0 B.1 C.2 D.3 2.(2020· 杭州高一检测 ) 函数 f(x)=(x-1) 2 -log a x( 其中 a>1) 零点的个数是 ( 　　 ) A.0 B.1 C.2 D.3 3. 定义在 R 上的奇函数 f(x) 满足 f(x)=x 2 -2x(x≥0) ，则函数 f(x) 的零点个数为 ( 　　 ) A.0 B.1 C.2 D.3 【 思路导引 】 1. 求出零点个数判断 . 2. 不能用代数法求零点时利用图象交点个数判断 . 3. 先求出 x≥0 时的零点，再利用奇偶性判断 x<0 时的零点 . 【 解析 】 1. 选 D. 函数 f(x)=x 3 -x=x(x+1)(x-1)=0 ，解得 x=0 或 x=1 或 x=-1. 函数 f(x)=x 3 -x 的零点的个数是 3. 2. 选 C. 函数 f(x)=(x-1) 2 -log a x( 其中 a>1) 零点的个数就是 (x-1) 2 -log a x=0 根的个数， 也就是两个函数 y=(x-1) 2 与 y=log a x( 其中 a>1) 图象的交点个数 . 因为 y=(x-1) 2 关于 x=1 对称， x=1 时取得最小值 0 ， y=log a x( 其中 a>1) 是增函数， x=1 时 y=0 ，所以两个函数 y=(x-1) 2 与 y=log a x( 其中 a>1) 图象的交点个数为 2. 3. 选 D. 当 x≥0 时， f(x)=x 2 -2x=0 可得， x=0 或 x=2 ，因为 f(x) 为奇函数，所以 f(-2)=-f(2)=0 ，从而函数 f(x) 有 3 个零点： 0 ， 2 ， -2. 【 解题策略 】 关于函数零点个数的判断 (1) 能直接求出零点的直接求零点判断； (2) 利用函数的图象判断零点个数 ①原理：函数的零点个数⇐方程的根的个数⇐移项拆分为两个初等函数，函数交点个数； ②关键：拆分成的两个函数应方便作图 . 【 跟踪训练 】 (2020· 宝鸡高一检测 ) 已知函数 f(x)= 则函数 f(x) 的零点个 数为 ( 　　 ) A.1 B.2 C.3 D.4 【 解析 】 选 C. 当 x≤1 时， 令 f(x)=0 ，得 x 2 + x=0 ， 解得 x=- 或 x=0 ； 当 x>1 时， 令 f(x)=0 ， 得 ln x- x+3=0 ， 故 ln x+3= x ， 在同一直角坐标系中分别作出 y=ln x+3 ， y= x 的图象如图所示， 观察可知，有 1 个交点，即 f(x)=0 在 (1 ， +∞) 上有 1 个解；综上所述，函数 f(x) 的零点个数为 3. 【 拓展训练 】 (2020· 朝阳高一检测 ) 已知函数 f(x)= 其中 k≥0. (1) 若 k=2 ，则 f(x) 的最小值为 _______ ；  (2) 关于 x 的函数 y=f(f(x)) 有两个不同零点，则实数 k 的取值范围是 _______.  【 解析 】 (1) 若 k=2 ，则 f(x)= 作函数 f(x) 的图象如图所示， 显然，当 x=0 时，函数 f(x) 取得最小值， 且最小值为 f(0)=-1. (2) 令 m=f(x) ，显然 f(m)=0 有唯一解 m=1 ， 由题意， f(x)=1 有两个不同的零点， 由图观察可知， k<1 ，又 k≥0 ，则实数 k 的取值范围为 0≤k<1. 答案： (1)-1 　 (2)[0 ， 1) 类型三　零点存在定理的应用 ( 数学运算、逻辑推理 ) 　角度 1 　判断零点所在的区间  【 典例 】 (2020· 菏泽高一检测 ) 函数 f(x)=log 8 x- 的一个零点所在的区间 是 ( 　　 ) A.(0 ， 1) B.(1 ， 2) C.(2 ， 3) D.(3 ， 4) 【 思路导引 】 代入端点值判断符号关系 . 【 解析 】 选 B. 函数 f(x)=log 8 x- 是连续增函数，因为 f(1)=0- <0 ， f(2)=log 8 2- >0 ，可得 f(1)f(2)<0 ， 所以函数 f(x) 的其中一个零点所在的区间是 (1 ， 2). 【 变式探究 】 本例中区间 (0 ， 1) 的端点 0 能代入函数解析式吗？怎样判断在该区间内是否有零点？ 【 解析 】 因为函数的定义域为 ( 0,+∞) , 因此 0 不能代入函数的解析式 . 当 x→0 时， log 8 x→-∞ ， → -∞ ， 所以 f(x)→-∞. 又 <0 ， 故在区间 (0 ， 1) 上不存在零点 . 角度 2 　由零点所在的区间求范围  【 典例 】 函数 f(x)=x 2 -2x+a 在区间 (1 ， 3) 内有一个零点，则实数 a 的取值范围是 ( 　　 ) A.(-3 ， 0) B.(-3 ， 1) C.(-1 ， 3) D.(-1 ， 1) 【 思路导引 】 求出二次函数的对称轴，利用图象确定条件求范围 . 【 解析 】 选 B. 因为 f(x)=x 2 -2x+a ，它的对称轴为 x=1 ，所以函数 f(x) 在区间 (1 ， 3) 内单调递增， 因为方程 x 2 -2x+a=0 在区间 (1 ， 3) 内有一个零点， 所以函数 f(x) 在区间 (1 ， 3) 内与 x 轴有一个交点， 根据零点存在定理得出： 即 解得 -30 ， f(2)=e 2 -2- >0 ， f(e)=e e -e- >0 ， 可得 f(x) 在 (0 ， 1) 内存在零点 . 2.(2020· 宿迁高一检测 ) 已知函数 f(x)=ln x+x-6 的零点 x 0 ∈(k ， k+1) ，则整数 k 的值为 _______.  【 解析 】 由函数的解析式可得函数在 (0 ， +∞) 上是增函数，且 f(4)=ln 4+4-6<0 ， f(5)=ln 5+5-6>0 ，故有 f(4)f(5)<0 ， 根据函数零点存在定理可得函数在区间 (4 ， 5) 上存在零点 . 结合所给的条件可得， k=4 ， 答案： 4 课堂检测 · 素养达标 1. 函数 f(x)=log 2 (2x+1) 的零点是 ( 　　 ) A.1 B.0 C.(0 ， 0) 　 D.(1 ， 1) 【 解析 】 选 B. 令 log 2 (2x+1)=0 ，解得 x=0. 2. 方程 e x +8x-8=0 的根所在的区间为 ( 　　 ) A.(-2 ， -1) B.(-1 ， 0) C.(0 ， 1) D.(1 ， 2) 【 解析 】 选 C. 令函数 f(x)=e x +8x-8 ，则方程 e x +8x-8=0 的根即为函数 f(x) 的零点， 再由 f(0)=1-8=-7<0 ，且 f(1)=e>0 ，可得函数 f(x) 在 (0 ， 1) 上有零点 . 3.( 教材二次开发：练习改编 ) 函数 f(x)=e x +3x+1 的零点所在的区间为 ( 　　 ) A.(-2 ， -1) B. C. D. 【 解析 】 选 B. 函数 f(x)=e x +3x+1 是连续函数， 因为 f(-1)=e -1 -3+1<0 ， +1>0 ， 故函数的零点所在的区间为 . 4. 函数 y=x 2 -bx+1 有一个零点，则 b=_______.  【 解析 】 因为函数有一个零点，所以 Δ=b 2 -4=0 ， 所以 b=±2. 答案： ±2 5. 函数 f(x)=(x+1)(x 2 +3x-10) 的零点有 _______ 个 .  【 解析 】 因为 f(x)=(x+1)(x 2 +3x-10) =(x+1)(x+5)(x-2) ， 所以由 f(x)=0 得 x=-5 或 x=-1 或 x=2. 答案： 3 函数的零点 与方程的解 核心知识 方法总结 易错提醒 核心素养 直观想象：通过确定函数零点个数及所在区间，培养直观想象的核心素养 应用函数零点存在定理时注意函数图象的连续性 数形结合：借助函数图象与 x 轴交点确定零点及方程的根 转化法：函数的零点转化为方程的根，转化为函数图象与 x 轴的交点 函数零点的定义 函数零点、方程的根、函数的图象与 x 轴交点的关系 函数的零点存在定理