江西省信丰中学2020届高三数学上学期周考十五理B层（含解析） 5页

- 1 - 江西省信丰中学 2020 届高三数学上学期周考十五（理 B 层） 一、选择题（每题 5 分，共 40 分） 1．如图，在 ABC 中， 2 3AD AC  ， 1 3BP BD  ，若 AP AB AC     ，则   的值 为（ ） A． 8 9 B． 4 9 C． 8 3 D． 4 3 2．在 ABC 中， BC 边上的中线 AD 的长为3， 2 6BC  ，则 AB AC   （ ） A． 1 B．1 C． 2 D．3 3．已知等比数列 na 的前 n 项和为 nS ，且 5 4S  ， 10 10S  ，则 15S  （ ） A．16 B．19 C．20 D．25 4．在数列 na 中，若 1 1a  ，  1 2 3n na a n N      ，则 101a  （ ） A． 1002 3 B． 1012 3 C． 1022 1 D． 1022 3 5．已知三棱锥 A BCD 的所有顶点都在球O 的球面上， AD  平面 ABC ， 90BAC  ， 2AD  ，若球O 的表面积为 29 ，则三棱锥 A BCD 的侧面积的最大值为（ ） A． 255 2 4  B． 5 415 2 4  C． 276 3 2  D． 2510 2 2  6．在△ ABC 中，若 30A   ， 8a  ， 8 3b  ，则 ABCS 等于（ ） A．32 3 B．16 3 C．32 3 或16 3 D．12 3 7．若数列 na 满足 1 12 5 2 3 n na a n n     ，且 1 5a  ，则数列 na 的前100项中，能被5整除 的项数为（ ） A． 42 B． 40 C． 30 D． 20 8.某几何体的三视图如右图所示,则该几何体外接球表面积为( ) A． 11 B．14 3  C． 28 3  D． 16 - 2 - 二．填空题（本大题共 4 小题，每题 5 分，共 20 分） 9．已知三棱锥 P ABC 的各顶点均在半径为 2 的球面上，且 3, 3, 2 3AB BC AC   ， 则三棱锥 P ABC 体积的最大值为______. 10．如图，在直角梯形 SDCB 中， / /SD CB ，CD SD ， 7SD  ， 4BC  ， 4DC  ， A 在线段 SD 上，E 是线段 AB 的中点，沿 AB 把平面 SAB 折起到平面 PAB 的位置，使 PA  平 面 ABCD ，则下列命题正确的编号为______. ①点 E 到平面 PDC 的距离为12 5 ； ②设折起后几何体的棱 PD 的中点 F ，则 / /AF 平面 PEC ； ③ 8D PECV   ； ④四棱锥 P ABCD 的内切球的表面积为 4 . 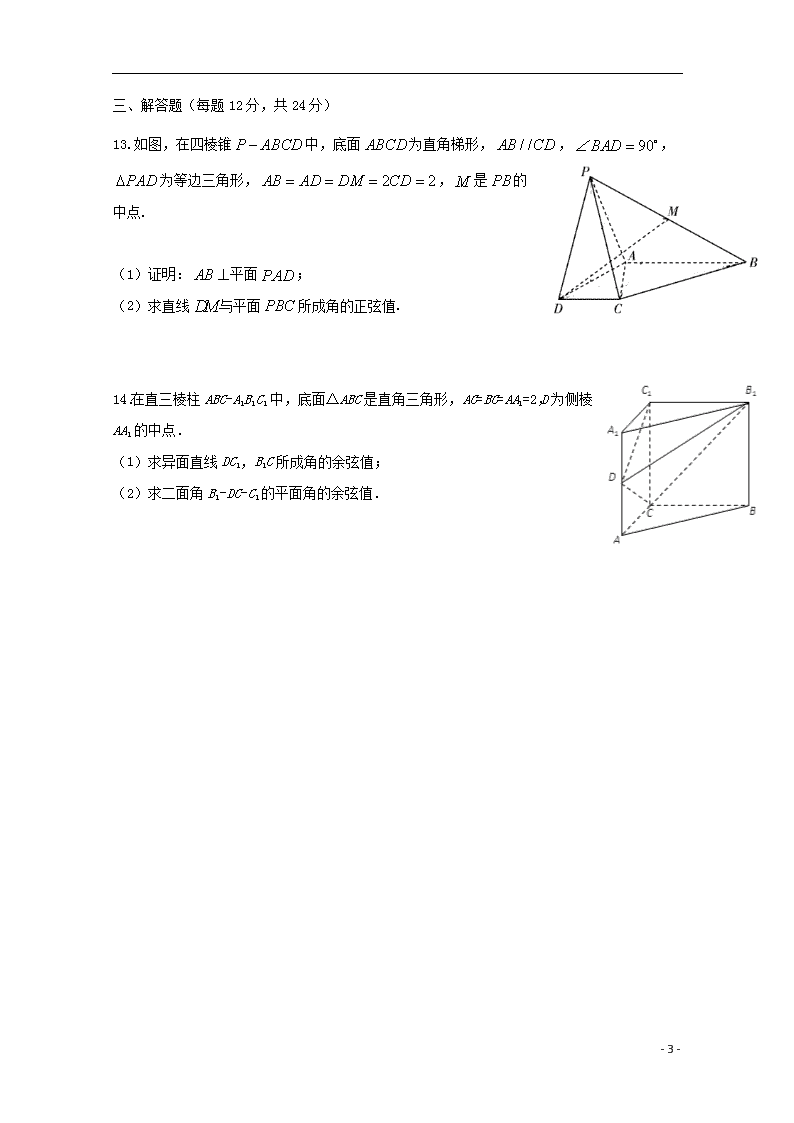11.已知四棱锥 P﹣ABCD 满足 PA＝PB＝PC＝PD＝AB＝2，且底面 ABCD 为正方形，则该四棱锥的 外接球的体积为_____． 12．如图，三棱锥 A BCD 的顶点 A ， B ， C ， D 都在同一球面上， BD 过球心 O 且 2 2BD  ， ABC△ 是边长为 2 等边三角形，点 P 、Q 分别为线段 AO ，BC 上的动点 （不含端点），且 AP CQ ，则三棱锥 P QCO 体积的最大值为_______． - 3 - 三、解答题（每题 12 分，共 24 分） 13.如图，在四棱锥 P ABCD 中，底面 ABCD 为直角梯形， / /AB CD ， 90BAD   ， PAD 为等边三角形， 2 2AB AD DM CD    ， M 是 PB 的 中点. （1）证明： AB  平面 PAD ； （2）求直线 DM与平面 PBC 所成角的正弦值. 14．在直三棱柱 ABC-A1B1C1 中，底面△ABC 是直角三角形，AC=BC=AA1=2，D 为侧 棱 AA1 的中点． （1）求异面直线 DC1，B1C 所成角的余弦值； （2）求二面角 B1-DC-C1 的平面角的余弦值． - 4 - 信丰中学理科数学周考十五答案 一．选择题(每小题 5 分，共 40 分） 题号 1 2 3 4 5 6 7 8 答案 A D B D A C B C 二．填空题： 9. 3 3 2 10 .①②③④ 11. 8 2 3  12. 1 12 三．解答题 13.（1）取 PA 的中点 N，连结 MN，DN， ∵M，N 分别是 PB，PA 的中点， ∴MN∥AB，且 MN 1 2  AB＝1， ∵DN 3 ，DM＝2，∴DN2+MN2＝DM2， ∴DN⊥MN，∴AB⊥DN， ∵AB⊥AD，AD∩DN＝D，∴AB⊥平面 PAD. （2）如图，连结 BD，CM，由（Ⅰ）知 AB⊥平面 PAD，∴AB⊥PA， 在 Rt△PAB 中，PB＝2 2 ，同理 PC 5 ， 在梯形 ABCD 中，BC 5 ，BD＝2 2 ， ∵PC＝BC，M 为 PB 的中点，∴CM⊥PB， 由题意得 S△PCB 1 1 2 2 3 62 2PB CM       ， 1 2BCDS CD AD    1， 设 O 为 AD 的中点，连结 PO，由题意得 PO⊥AD， ∵平面 PAD⊥平面 ABCD，PO⊂平面 PAD，平面 PAD∩平面 ABCD＝AD， ∴PO⊥平面 ABCD， 设点 D 到平面 PBC 的距离为 d， ∵VP﹣BCD＝VD﹣PCB，∴ 1 1 3 3DCB PCBS PO S d      ，解得 d 2 2  ． - 5 - ∵DM＝2，∴直线 DM 与平面 PBC 所成角的正弦值 sinθ 2 4 d DM   14.【答案】（1） 10 10 （2） 2 3 （1）如图所示，以 C 为原点，CA、CB、CC1 为坐标轴，建立空间直角坐标系 C﹣xyz． 则 C（0，0，0），A（2，0，0），B（0，2，0），C1（0，0，2），B1（0，2，2），D（2，0， 1）． 所以 1DC  （﹣2，0，1）， 1B C  （0，﹣2，﹣2）． 所以 cos 1 1 1 1 1 1 2 10 105 8 DC B CDC B C DC B C          ＜ ， ＞ ． 即异面直线 DC1 与 B1C 所成角的余弦值为 10 10 ． （2）因为CB  （0，2，0）， CA  （2，0，0）， 1CC  （0，0，2）， 所以CB  •CA  0，CB  • 1CC  0， 所以CB  为平面 ACC1A1 的一个法向量． 因为 1B C  （0，﹣2，﹣2），CD  （2，0，1）， 设平面 B1DC 的一个法向量为 n，n＝（x，y，z）． 由 1 0 0 n B C n CD        ，得 2 2 0 2 0 y z x z       令 x＝1，则 y＝2，z＝﹣2，n＝（1，2，﹣2）． 所以 cos＜n， 4 2 3 2 3 n CBCB n CB     ＞ ． 所以二面角 B1﹣DC﹣C1 的余弦值为 2 3 ．