2021版高考数学一轮复习第四章三角函数解三角形4-4三角函数的图象与性质练习苏教版 11页

- 1 - 4.4 三角函数的图象与性质 考点一 三角函数的定义域、值域(最值) 1.函数 y= 的定义域为________. 2.(2019·全国卷Ⅰ)函数 f(x)=sin -3cos x 的最小值为________. 3.函数 f(x)=1-3sin 的值域为________. 【解析】1.要使函数有意义,必须使 sin x-cos x≥0.利用图象,在同一坐标系中画出[0,2π] 上 y=sin x 和 y=cos x 的图象.在[0,2π]内,满足 sin x=cos x 的 x 为 , ,再结合正弦、 余弦函数的周期是 2π,所以原函数的定义域为 . 答案: 2.f(x)=sin -3cos x=-cos 2x-3cos x =-2cos2x-3cos x+1=-2 + , 因为-1≤cos x≤1,所以当 cos x=1 时,f(x)min=-4, 故函数 f(x)的最小值为-4. 答案:-4 - 2 - 3.因为-1≤sin ≤1,所以-3≤-3sin ≤3, 所以-2≤1-3sin ≤4, 所以函数 f(x)=1-3sin 的值域为[-2,4]. 答案:[-2,4] 1.求三角函数的定义域的实质 解简单的三角不等式,常借助三角函数线或三角函数的图象求解. 2.求解三角函数的值域(最值)常见三种类型 (1)形如 y=asin x+bcos x+c 的三角函数化为 y=Asin(ωx+φ)+c 的形式,再求值域(最值). (2)形如 y=asin2x+bsin x+c 的三角函数,可先设sin x=t,化为关于 t的二次函数求值域(最值). (3)形如 y=asin xcos x+b(sin x±cos x)+c 的三角函数,可先设 t=sin x±cos x,化为关于 t 的二次函数求值域(最值). 【秒杀绝招】 图象性质解 T1,sin x-cos x= sin ≥0,将 x- 视为一个整体,由正弦函数 y=sin x 的图象与性质知 2kπ≤x- ≤π+2kπ(k∈Z),解得 2kπ+ ≤x≤2kπ+ (k∈Z). 所以定义域为 . 特殊值法解 T2,易知 f(x)≥-4,又 x=0 时,f(x)=-4,所以 f(x)的最小值为-4. 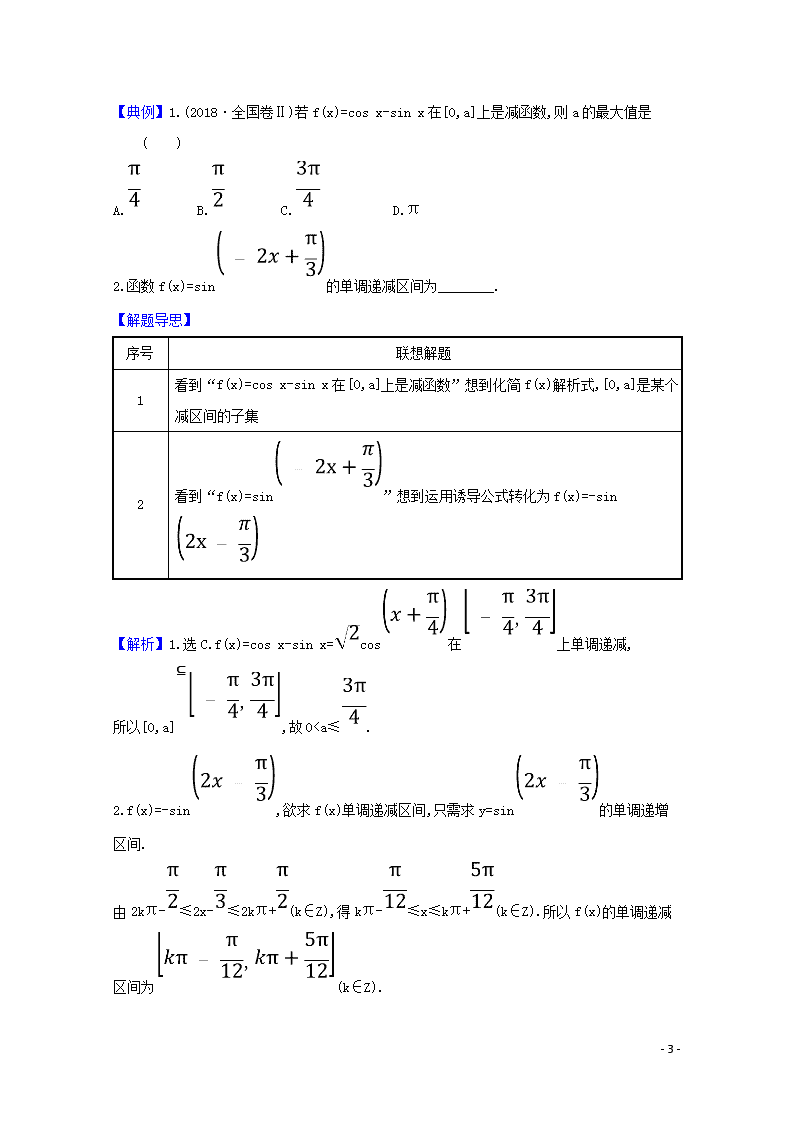考点二 三角函数的单调性 【典例】1.(2018·全国卷Ⅱ)若 f(x)=cos x-sin x 在[0,a]上是减函数,则 a 的最大值是 ( ) - 3 - A. B. C. D.π 2.函数 f(x)=sin 的单调递减区间为________. 【解题导思】 序号 联想解题 1 看到“f(x)=cos x-sin x 在[0,a]上是减函数”想到化简 f(x)解析式,[0,a]是某个 减区间的子集 2 看到“f(x)=sin ”想到运用诱导公式转化为 f(x)=-sin 【解析】1.选 C.f(x)=cos x-sin x= cos 在 上单调递减, 所以[0,a]⊆ ,故 00)的形式,再求 y=Asin(ωx+φ)的单调区间,只需把ωx+φ看 作一个整体代入 y=sin x 的相应单调区间内即可. 2.已知单调区间求参数的三种方法 子集法 求出原函数的相应单调区间,由已知区间是该区间的子集,列不等式(组)求解 求补 集法 由所给区间求出整体角的范围,由该范围是某相应正、余弦函数的某个单调区间 的子集,列不等式(组)求解 周期 性法 由所给区间的两个端点到其相应对称中心的距离不超过 周期列不等式(组)求解 1.设函数 f(x)=sin ,x∈ ,则以下结论正确的是 ( ) A.函数 f(x)在 上单调递减 - 5 - B.函数 f(x)在 上单调递增 C.函数 f(x)在 上单调递减 D.函数 f(x)在 上单调递增 【解析】选 C.由 x∈ 得 2x- ∈ ,所以 f(x)先减后增; 由 x∈ 得 2x- ∈ , 所以 f(x)先增后减; 由 x∈ 得 2x- ∈ , 所以 f(x)单调递减; 由 x∈ 得 2x- ∈ ,所以 f(x)先减后增. 2.若函数 f(x)=sin ωx(ω>0)在区间 上单调递增,在区间 上单调递减,则ω =________. 【解析】因为 f(x)=sin ωx(ω>0)过原点, 所以当 0≤ωx≤ ,即 0≤x≤ 时, y=sin ωx 是增函数; - 6 - 当 ≤ωx≤ ,即 ≤x≤ 时,y=sin ωx 是减函数. 由已知 = ,所以ω= . 答案: 考点三 三角函数的周期性、奇偶性、对称性 命 题 精 解 读 考什么:(1)周期性,奇偶性、对称性等. (2)考查逻辑推理,数学运算等核心素养,以及转化与化归的思想. 怎么考:与诱导公式、三角恒等变换结合考查求周期,参数等等. 新趋势:以考查与诱导公式、三角恒等变换结合为主. 学 霸 好 方 法 求周期的三种方法 (1)利用周期函数的定义: f(x+T)=f(x). (2)利用公式:y=Asin(ωx+φ)和 y=Acos(ωx+φ)的最小正周期为 ,y=tan(ωx+ φ)的最小正周期为 . (3)利用图象:图象重复的 x 轴上一段的长度. ①正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的 对称中心与对称轴之间的距离是 个周期. ②正切曲线相邻两对称中心之间的距离是半个周期. 周期性 【典例】1.(2019·全国卷Ⅱ)若 x1= ,x2= 是函数 f(x)=sin ωx(ω>0)两个相邻的极值点, 则ω= ( ) - 7 - A.2 B. C.1 D. 2.(2019·北京高考)函数 f(x)=sin22x 的最小正周期是________. 【解析】1.选 A.由于 x1= ,x2= 是函数两个相邻的极值点,故 = - = , 所以 T=π,即ω= =2. 2.f(x)= (1-cos 4x),最小正周期 T= = . 答案: 涉及三角函数的性质问题有哪些注意事项? 提示:(1)考虑利用三角恒等变换将函数化为一个角的一种函数形式. (2)掌握一些简单函数的周期:如: ①y=Asin(ωx+φ)的周期为 . ②y=Atan(ωx+φ)的周期为 . ③y=|sin x|的周期为π. ④y=|tan x|的周期为π. 奇偶性、对称性 【典例】(2019·全国卷Ⅱ)下列函数中,以 为周期且在区间 单调递增的是 ( ) A.f(x)=|cos 2x| B.f(x)=|sin 2x| C.f(x)=cos|x| D.f(x)=sin|x| - 8 - 【解析】选 A.分别画出函数的图象可得选项 A 的周期为 ,选项 B 的周期为 ,而选项 C 的周 期为 2π,选项 D 不是周期函数.结合图象的升降情况可得 A 正确. 1.函数 y= sin 2x+cos 2x 的最小正周期为 ( ) A. B. C.π D.2π 【解析】选 C.y= sin 2x+cos 2x=2sin ,T= =π. 2.同时具有:①最小正周期为π;②图象关于点 对称的一个函数 是 ( ) A.y=cos B.y=sin C.y=sin D.y=tan 【解析】选 D.由 T=π,排除 C; 把 x= 代入 A,B,函数值均不为零,排除 A,B; 再验证 D 符合题意. 3.(2018·江苏高考)已知函数 y=sin(2x+φ) 的图象关于直线 x= 对称, 则φ的值是________. 【解析】正弦函数的对称轴为 +kπ(k∈Z), - 9 - 故把 x= 代入得 +φ= +kπ(k∈Z),φ=- +kπ(k∈Z),因为- <φ< , 所以 k=0,φ=- . 答案:- 1.函数 f(x)=cos(ωx+φ)的部分图象如图所示,则 f(x)的单调递减区间 为 ( ) A. ,k∈Z B. ,k∈Z C. ,k∈Z D. ,k∈Z 【解析】选 D.由五点法作图知, - 10 - 解得 所以 f(x)=cos , 令 2kπ<πx+ <2kπ+π,k∈Z, 解得 2k-