数学人教B版必修4教案：3-1-1 两角和与差的余弦公式3 Word版含答案 6页

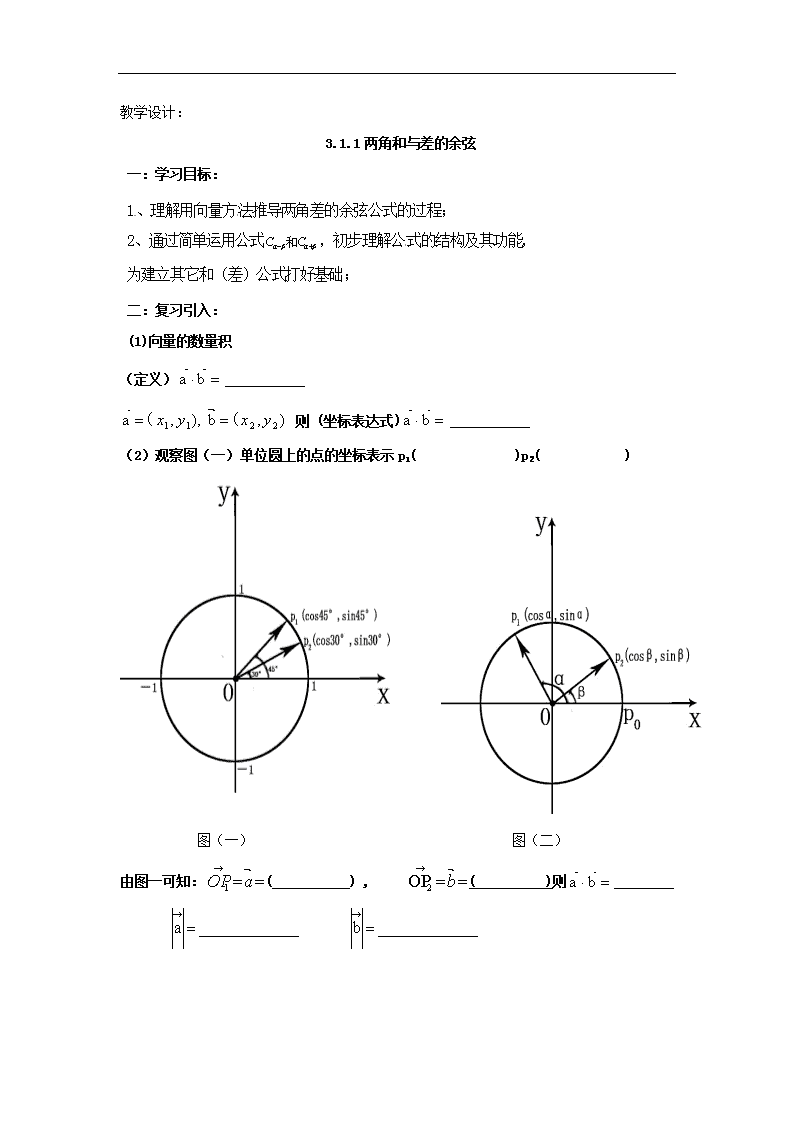
教学设计： 3.1.1 两角和与差的余弦 一：学习目标： 1、理解用向量方法推导两角差的余弦公式的过程； 2、通过简单运用公式C C    和 ，初步理解公式的结构及其功能， 为建立其它和（差）公式打好基础； 二：复习引入： (1)向量的数量积 （定义） __________ba  ),,a 11 yx（ ),b 22 yx（ 则 (坐标表达式) __________ba  （2）观察图（一）单位圆上的点的坐标表示 p1( )p2( ) 图（一） 图（二） 由图一可知：   aOP1 ( ) ,   b2OP ( )则  ba _____________a   _____________b   三：合作探究 各小组交流以下问题 问题 1：150 可以用那两个特殊角表示？ 问题 2：cos150= cos(450-300)=cos450 –cos300 成立吗？ 问题 3：由图（一）  )3045cos(Pcos 21OP   aOP1 ( ) ,   b2OP ( )则  ba _____________a   _____________b   由定义  a b __________ cos    所以  )3045cos(Pcos 21OP 问题4 ：由  30sin45sin30cos45cos)3045cos( 出发，你能推广到对任意的 两个角都成立吗？根据图二如何推导？ 问题 5：两角和的余弦公式如何推导？ 提示：令   结论： ）（两角和与差的余弦公式  C 注： 1. 2. 3. 结构特点： 四． 互相交流，小组活动 公式应用闯关 第一关：小试身手 请用特殊角分别代替公式中α、β，你能求哪些非特殊角的值呢？（选择的特殊角可以 是 30°60°45°等）请每组自行选择两个特殊角计算和与差的余弦 (1) (2) 第二关：再接再厉 若β固定，分别用 2 π,π 代替α，你将会发现什么结论呢？ (1)cos( ) ___________(2)cos( ) ___________ (3)cos( ) __________(4)cos( ) ___________2 2                第三关：各显神通 倘若让你对 C(α±β)公式中的α、β自由赋值，你又将发现什么结论呢？ (1)cos __________4   （ ） ；(2)cos ____________  （ ） (3)   ____)____)sin(______sin(_cos(_____)(_____)coscos   ）（ (4)   ___)___)sin(______sin(__cos(_____)cos(_____)cos  ）（）（  第四关：逆向训练 1、化简求值：cos 80°cos 20°＋sin80°sin20°. 2、化简求值：sin15°cos75°＋cos15°sin105° 第五关：活学活用 2、已知 )2 3,(,5 3cos),,2(,3 2sin   ，求 )cos(   的值。 规律总结： 五．达标检测：    31、已知 cos ,求 cos( )。5 4      23、已知 cos( )= ， ( , ),求 cos 。4 10 2                           2 0 2 1 cos 27 cos 57 sin 27 cos 147 2 cos 15 sin 15 3 cos 20 cos 25 sin 20 sin(25 ) 1 34 cos ,cos( ) ,2 7 5 cos 、 － 、 － 、 （ x） x － （ x） x 、已知 、 （0， ） 求 的值。 六．课堂小结：小组讨论总结这节课你获得了哪些知识、技能与方法？ 七． 作业布置 八． 板书设计 课题：3.1.1 两角和与差的 余弦 两角差的余弦公式 c o s ( ) c o s c o s s in s in          两角和的余弦公式 c o s ( ) c o s c o s s in s in          白板 例题 九． 教后反思： 3+ ) - ) - - ( , )2 3+ ( ,2 ) 22                       必做题：本节课后习题 4选作题：已知cos( = ,cos( = , ,5 5 ,求cos . 思考题：在学习了cos( )后，想一想sin( )是否 也有同样的规律？tan( )呢？