【新教材】2020-2021学年高中人教A版数学必修第二册课件：6-4-3　第2课时　正弦定理 27页

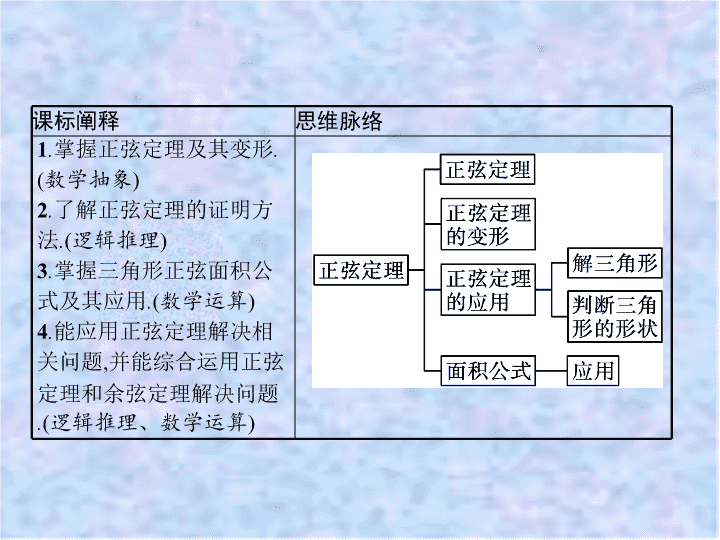
第 2 课时　正弦定理 课标阐释 思维脉络 1 . 掌握正弦定理及其变形 . ( 数学抽象 ) 2 . 了解正弦定理的证明方法 . ( 逻辑推理 ) 3 . 掌握三角形正弦面积公式及其应用 . ( 数学运算 ) 4 . 能应用正弦定理解决相关问题 , 并能综合运用正弦定理和余弦定理解决问题 . ( 逻辑推理、数学运算 ) 激趣诱思 知识点拨 从金字塔的建造到尼罗河两岸的土地丈量 , 从大禹治水到都江堰的修建 , 从天文观测到精密仪器的制造 , 都离不开对几何图形的测量、设计和计算 . 测量河流两岸码头之间的距离 , 确定待建隧道的长度 , 确定卫星的角度与高度等问题 , 都可以转化为求三角形的边与角的问题 , 这就需要我们进一步探索三角形的边角关系 , 通常我们是通过正弦定理与余弦定理来研究三角形中的边角关系的 , 这一节我们来学习 —— 正弦定理 . 激趣诱思 知识点拨 知识点一、正弦 定理 1 . 名师点析 正弦定理解三角形的常见类型 (1) 已知三角形的两边及一边所对的角 , 求剩余的边和角 . (2) 已知两角和任一边 , 求另外两边和一角 . 激趣诱思 知识点拨 答案 : (1)4 　 (2)45 ° 激趣诱思 知识点拨 知识点二、正弦定理的变形 正弦定理的变形 ( R 为 △ ABC 外接圆的半径 ) (1) a= 2 R sin A , b= 2 R sin B , c= 2 R sin C ; (2)sin A= ,sin B= ,sin C= ; (3) a ∶ b ∶ c= sin A ∶ sin B ∶ sin C . 答案 : 45° 或 135 ° 激趣诱思 知识点拨 知识点三、三角形的面积 公式 名师点析 三角形面积公式的其他 形式 激趣诱思 知识点拨 微练习 (1) 在 △ ABC 中 , 若 AB= 3, BC= 4, B= 120°, 则 △ ABC 的面积等于 　　　　　 .  (2) 在 △ ABC 中 , 若 a= 2, b= 8, S △ ABC = 4, 则 C= 　　　　 .  探究一 探究二 探究三 探究四 素养形成 当堂检测 已知两角和一边解三角形 例 1 在 △ ABC 中 , 已知 B= 30°, C= 105°, b= 4, 解三角形 . 分析 由三角形的内角和定理可求 A 的度数 . 根据正弦定理可求 a , c. 解 : 因为 B= 30°, C= 105°, 所以 A= 180° - ( B+C ) = 180° - (30° + 105°) = 45° . 反思感悟 已知两角及一边解三角形的解题方法 (1) 若所给边是已知角的对边 , 可先由正弦定理求另一边 , 再由三角形的内角和定理求出第三个角 , 最后由正弦定理求第三边 . (2) 若所给边不是已知角的对边 , 则先由三角形内角和定理求第三个角 , 再由正弦定理求另外两边 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 已知两边和其中一边的对角解三角形 例 2 在 △ ABC 中 , 已知 a= 2, b = , A= 45°, 解三角形 . 分析 先利用正弦定理求角 B , 再根据三角形的内角和定理求角 C , 最后利用正弦定理求边 c. 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 已知三角形的两边和其中一边的对角时解三角形的方法 (1) 首先由正弦定理求出另一边所对的角的正弦值 . (2) 当已知的角为大边所对的角时 , 由三角形中 “ 大边对大角 , 大角对大边 ” 的法则能判断另一边所对的角是锐角还是钝角 . (3) 当已知的角为小边所对的角时 , 不能判断另一边所对的角为锐角 , 这时由正弦值可求得两个角 , 要分类讨论 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 延伸探究 本例中 , 将条件改为 “ a= 5, b= 2, B= 120°”, 解三角形 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 判断三角形的形状 例 3 在 △ ABC 中 , 若 ( a-c cos B )sin B= ( b-c cos A )sin A , 判断 △ ABC 的形状 . 分析 探究一 探究二 探究三 探究四 素养形成 当堂检测 解 : ( 方法一 ) ∵ ( a-c cos B )sin B= ( b-c cos A )sin A , ∴ 由正弦定理、余弦定理 , 得 整理 , 得 ( a 2 +b 2 -c 2 ) b 2 = ( a 2 +b 2 -c 2 ) a 2 , 即 ( a 2 -b 2 )( a 2 +b 2 -c 2 ) = 0, ∴ a 2 +b 2 -c 2 = 0 或 a 2 =b 2 . ∴ a 2 +b 2 =c 2 或 a=b. 故 △ ABC 为直角三角形或等腰三角形 . ( 方法二 ) 根据正弦定理 , 原等式可化为 (sin A- sin C cos B )sin B = ( sin B- sin C cos A )sin A , 即 sin C cos B sin B= sin C cos A sin A. ∵ sin C ≠0, ∴ sin B cos B= sin A cos A. ∴ sin 2 B= sin 2 A. ∴ 2 B= 2 A 或 2 B+ 2 A= π , 即 A=B 或 A+B = . ∴△ ABC 是等腰三角形或直角三角形 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 三角形形状的判断方法 判断三角形的形状 , 就是根据题目条件 , 分析其是不是等腰三角形、直角三角形、等边三角形、等腰直角三角形、锐角三角形、钝角三角形等 . 利用正弦定理判断三角形形状的方法如下 : 探究一 探究二 探究三 探究四 素养形成 当堂检测 延伸探究 本例中 , 将条件改为 “ 在 △ ABC 中 , 若 ( a-a cos B )sin B= ( b-c cos C )sin A ”, 判断 △ ABC 的形状 . 解 : 因为 ( a-a cos B )sin B= ( b-c cos C )sin A , 所以 a sin B-a cos B sin B=b sin A-c cos C sin A , 而由正弦定理可知 a sin B=b sin A , 所以 a cos B sin B=c cos C sin A , 即 sin A cos B sin B= sin C cos C sin A , 所以 cos B sin B= sin C cos C , 即 sin 2 B= sin 2 C , 所以 2 B= 2 C 或 2 B+ 2 C= 180°, 即 B=C 或 B+C= 90°, 故 △ ABC 是等腰三角形或直角三角形 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 三角形面积公式的应用 例 4 计算下列各三角形的面积 . (1) 在 △ ABC 中 , a= 5, c= 3, B= 150°; (2) 在 △ ABC 中 , a= 8, b= 8 , A= 30 °; (3) 在 △ ABC 中 , a= 2, b= 3, c= 4 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 三角形面积的求解思路 求三角形面积时 , 由于三角形面积公式有不同形式 , 因此实际使用时要结合题目的条件灵活运用公式求解 . 当三角形的两边及其夹角都已知或能求出时 , 常 利用 探究一 探究二 探究三 探究四 素养形成 当堂检测 变式训练 2 (1) 在 △ ABC 中 , 若 A= 60°, b= 16, S △ ABC = 64 , 则 c= 　　　　 ;  (2) 在 △ ABC 中 , 已知 C= 120°, AB= 2 AC= 2 , 则 △ ABC 的面积等于 　　　　 .  探究一 探究二 探究三 探究四 素养形成 当堂检测 对三角形解的个数的探究 已知三角形的两角和任意一边 , 求其他的边和角 , 此时有唯一解 , 即当三角形的两角和任意一边确定时 , 三角形被唯一确定 . 已知三角形的两边和其中一边的对角 , 求其他的边和角 , 此时可能出现一解、两解或无解的情况 , 三角形不能被唯一确定 . 因此 “ 已知两边和其中一边的对角 , 求另一边的对角 ” 时 , 需要分析三角形解的情况 , 下面以已知 a , b 和角 A 解三角形为例进行说明 . 由正弦定理、正弦函数的有界性及三角形的性质可得 , 在 △ ABC 中 , 已知 a , b 和角 A 时 , 解的情况如下 : 探究一 探究二 探究三 探究四 素养形成 当堂检测 方法点睛 三角形解的个数也可由三角形中 “ 大边对大角 ” 来判定 . 设 A 为锐角 , 若 a ≥ b , 则 A ≥ B , 从而 B 为锐角 , 有一解 . 若 a 1, 即 a