上海教育高中数学一下正弦函数和余弦函数的图像与性质篇 19页

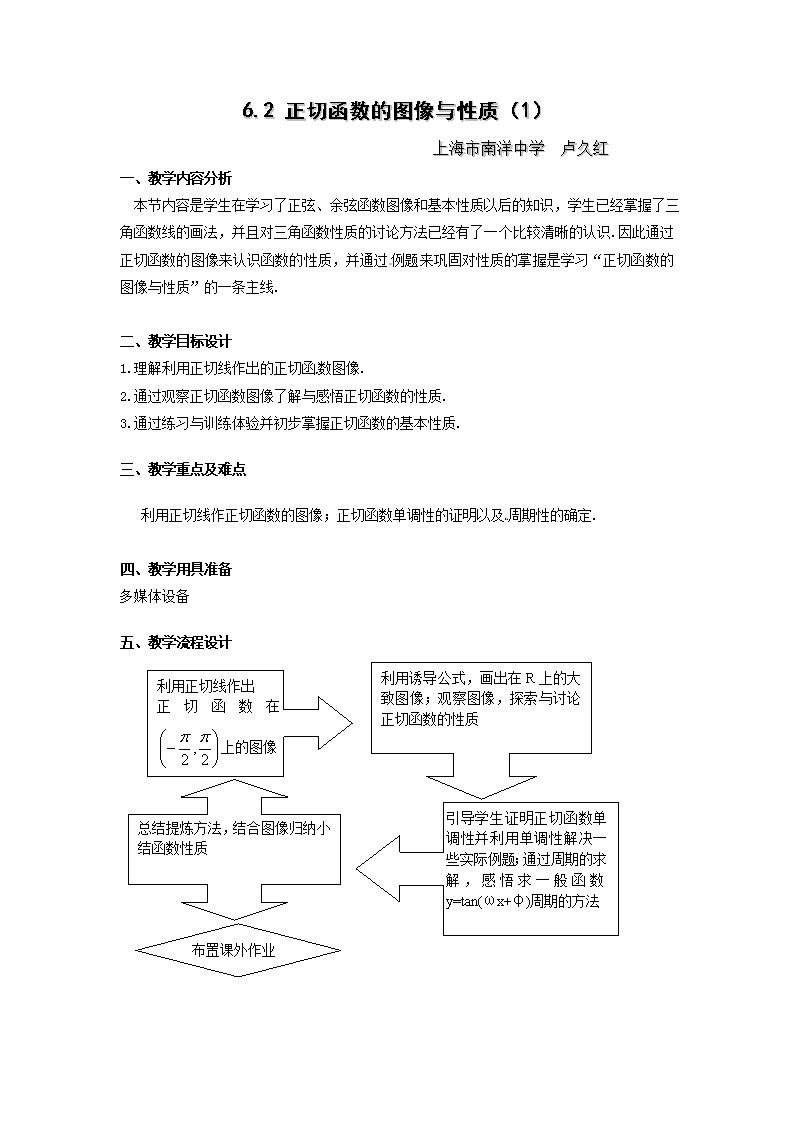
‎6.2 正切函数的图像与性质（1）‎ ‎ 上海市南洋中学 卢久红 一、教学内容分析 ‎ 本节内容是学生在学习了正弦、余弦函数图像和基本性质以后的知识，学生已经掌握了三角函数线的画法，并且对三角函数性质的讨论方法已经有了一个比较清晰的认识.因此通过正切函数的图像来认识函数的性质，并通过例题来巩固对性质的掌握是学习“正切函数的图像与性质”的一条主线.‎ 二、教学目标设计 ‎1.理解利用正切线作出的正切函数图像.‎ ‎2.通过观察正切函数图像了解与感悟正切函数的性质.‎ ‎3.通过练习与训练体验并初步掌握正切函数的基本性质.]‎ 三、教学重点及难点 ‎ 利用正切线作正切函数的图像；正切函数单调性的证明以及周期性的确定.‎ 四、教学用具准备 多媒体设备 利用诱导公式，画出在R上的大致图像；观察图像，探索与讨论正切函数的性质 利用正切线作出 正切函数在上的图像 五、教学流程设计 布置课外作业 总结提炼方法，结合图像归纳小结函数性质 引导学生证明正切函数单调性并利用单调性解决一些实际例题；通过周期的求解，感悟求一般函数y=tan(ωx+φ)周期的方法 六、教学过程设计 一、 复习引入 ‎ 1．复习 我们在前几节中学习了正弦函数线、余弦函数线以及正切函数线，我们通过正弦函数线，画出了正弦函数的图像，并研究了函数的性质.今天，我们同样按照这样的方法通过正切线来画出正切函数的图像，并研究和讨论它的性质.‎ ‎ 2．引入 y ‎ 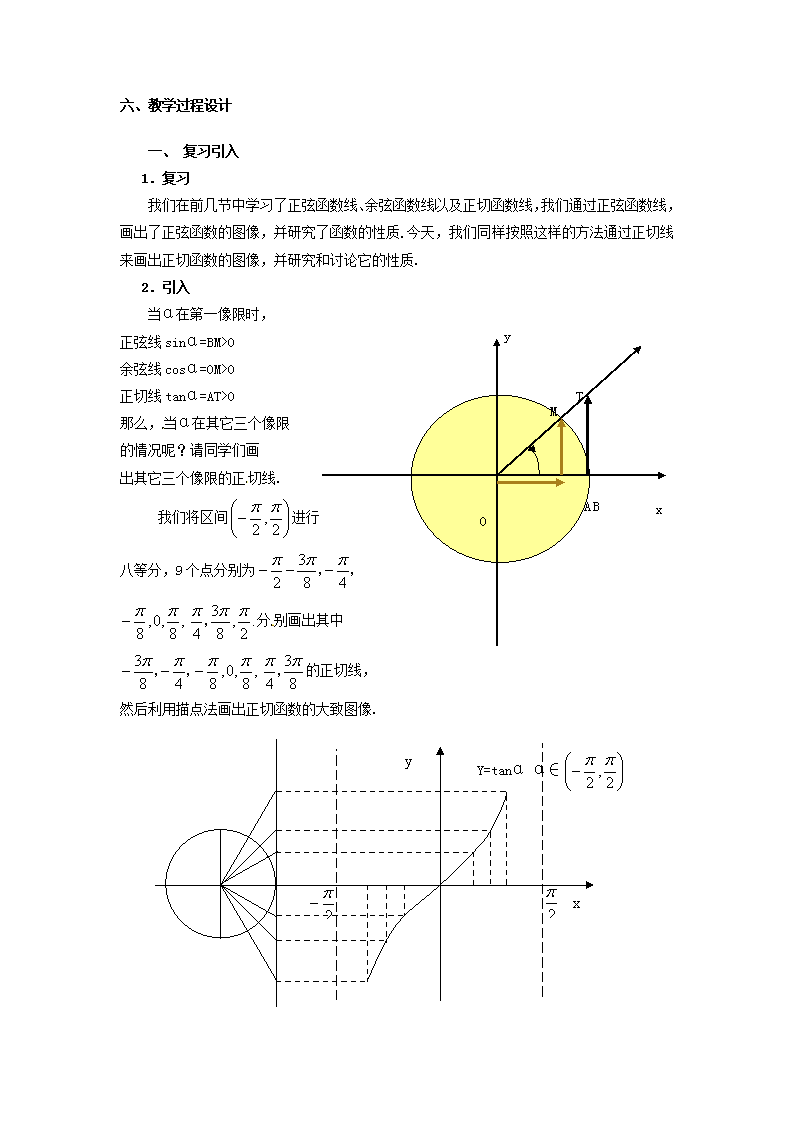当α在第一像限时， ‎ 正弦线sinα=BM>0‎ T 余弦线cosα=OM>0‎ M 正切线tanα=AT>0‎ 那么，当α在其它三个像限 的情况呢？请同学们画 A[:B x[来 出其它三个像限的正切线.‎ O 我们将区间进行 八等分，9个点分别为 分别画出其中 的正切线，‎ 然后利用描点法画出正切函数的大致图像.‎ Y=tanα α∈ ‎ x y 由正切三角比的诱导公式可知：‎ 那么y=，可知为y=tanx的一个周期 由此，我们可以画出y=tanx在R上的大致图像如下：‎ ‎0‎ y x 二、学习新课 1. 探究性质 观察正切函数的图像，引导学生得正切函数的性质：‎ ‎1.定义域：，‎ ‎2.值域：R ‎ 观察：当从小于，时，‎ ‎ 当从大于，时，.‎ ‎3.周期性：‎ ‎4.奇偶性：奇函数 ‎5.单调性：在开区间内，函数单调递增.‎ 从图像上看出函数y=tanx的单调区间是，但是我们怎样从理论上去加以证明呢？‎ 考察这个区间内的函数y=tanx的单调性.‎ 在这个区间内任意取，且，y1-y2=tanx1-tanx2‎ ‎==.‎ 因为，所以则cosx1、cosx2>0‎ sin()<0,从而tanx1-tanx2<0，y10.因此1+tanx1·tanx2>0.‎ 则tanx1-tanx2<0, tanx1