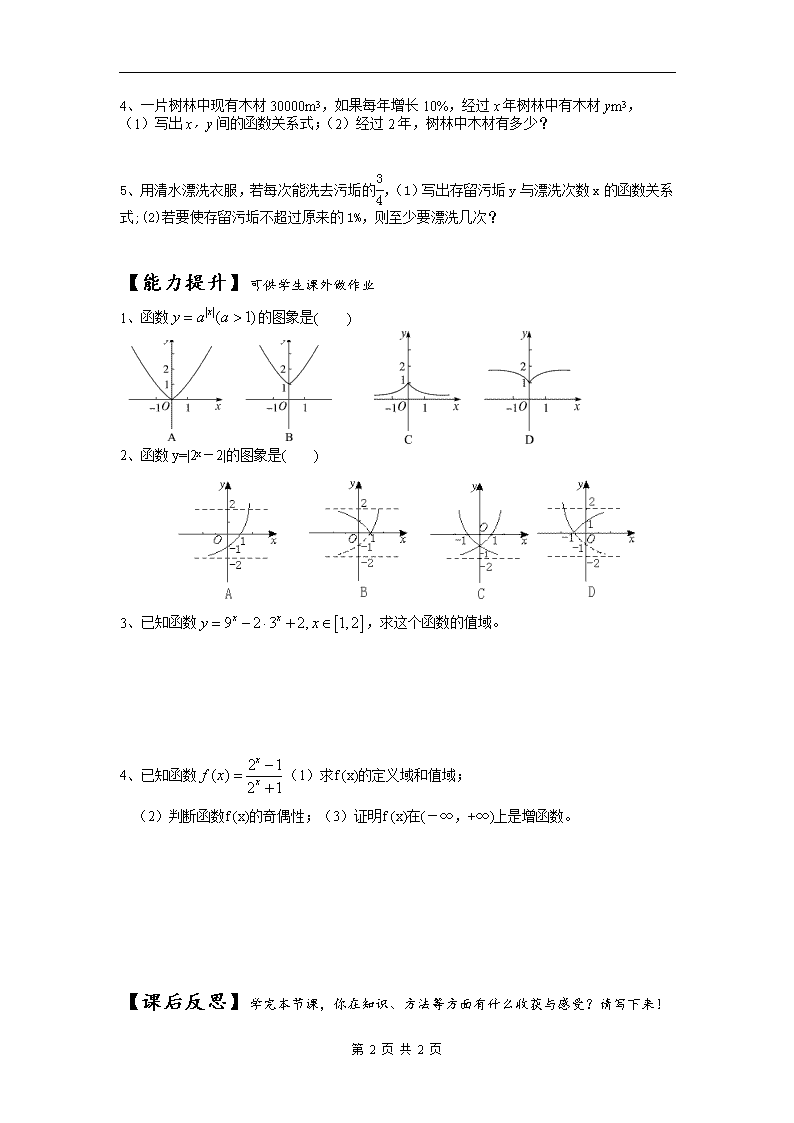《指数函数及其性质》导学案(1) 2页

‎ ‎ ‎《2.1.2 指数函数及其性质（2）》导学案 主编：段小文 班次 姓名 ‎ ‎【学习目标】其中2、3是重点和难点 ‎1.熟练掌握指数函数概念、图象、性质。‎ ‎2.掌握指数函数的性质及应用。‎ ‎3.理解指数函数的简单应用模型。‎ ‎【课前导学】预习教材第57-58页，找出疑惑之处，完成新知学习 ‎1、画出的函数图象。‎ 提问：通过函数的图象，你能说出底数与函数图象的位置关系吗？‎ ‎2、指数函数增长模型：原有量N，平均最长率p，则经过时间x后的总量y= 。‎ ‎3、形如 （a＞0且≠1）的函数是一种 ，这是非常有用的函数模型，注意：阅读教材例8，指数型函数的应用。‎ ‎【课中导学】首先独立思考探究，然后合作交流展示 探究一：你能说出底数与函数图象的位置关系吗？→请用一句话概括 例1、右图是指数函数①，②，③，④的图象，则a、b、c、d与1的大小关系是(　　) ‎ A．a＜b＜1＜c＜d B．b＜a＜1＜d＜c C．1＜a＜b＜c＜d D．a＜b＜1＜d＜c 探究二：如何应用函数模型解决问题？→强调数学应用思想 例2、我国人口问题非常突出，在耕地面积只占世界7%的国土上，却养育着22%的世界人口。因此，中国的人口问题是公认的社会问题。2000年第五次人口普查，中国人口已达到13亿，年增长率约为1%。为了有效地控制人口过快增长，实行计划生育成为我国一项基本国策。‎ ‎(Ⅰ)按照上述材料中的1%的增长率，从2000年起，x年后我国的人口将达到2000年的多少倍？‎ ‎(Ⅱ)从2000年起到2020年我国的人口将达到多少？‎ 探究三：指数形式的函数定义域、值域：‎ 例3、求下列函数的定义域、值域：，。‎ ‎【自我评价】你完成本节导学案的情况为（ ）‎ ‎ A.很好 B.较好 C.一般 D.较差 ‎【基础检测】当堂达标练习，（时量：5分钟 满分：10分）计分： ‎ ‎1、函数的定义域是 。‎ ‎2、当x∈［－2,0］时，函数的值域是 。‎ ‎3、若函数的图象不经过第一象限，则m的取值范围是 。‎ 第 2 页 共 2 页 ‎ ‎ ‎4、一片树林中现有木材30000m3，如果每年增长10%，经过x年树林中有木材ym3，‎ ‎（1）写出x，y间的函数关系式；（2）经过2年，树林中木材有多少？‎ ‎5、用清水漂洗衣服，若每次能洗去污垢的，（1）写出存留污垢y与漂洗次数x的函数关系式;(2)若要使存留污垢不超过原来的1%，则至少要漂洗几次？‎ ‎【能力提升】可供学生课外做作业 ‎1、函数的图象是(　　)‎ ‎ ‎ ‎2、函数y=|2x－2|的图象是( ) ‎3、已知函数，求这个函数的值域。‎ ‎4、已知函数（1）求f (x)的定义域和值域；‎ ‎ （2）判断函数f (x)的奇偶性；（3）证明f (x)在(－∞，+∞)上是增函数。‎ ‎【课后反思】学完本节课，你在知识、方法等方面有什么收获与感受？请写下来！‎ 第 2 页 共 2 页