2021高三数学人教B版一轮学案：第二章 第八节　函数与方程 11页

www.ks5u.com 第八节　函数与方程 最新考纲 考情分析 ‎1.结合二次函数的图象，了解函数的零点与方程根的联系，判断一元二次方程根的存在性及根的个数．‎ ‎2．根据具体函数的图象，能够用二分法求相应方程的近似解.‎ ‎1.函数零点个数、存在区间及方程解的确定与应用是高考热点．‎ ‎2．常与函数的图象与性质交汇命题，主要考查函数与方程、转化与化归、数形结合思想．‎ ‎3．题型以选择题和填空题为主，属中、高档题.‎ ‎　　　　　　　　　　　　　　　‎ 知识点一 　函数的零点 ‎1．函数零点的概念 对于函数y＝f(x)，把使f(x)＝0的实数x叫做函数y＝f(x)的零点．‎ ‎2．函数零点与方程根的关系 方程f(x)＝0有实数根⇔函数y＝f(x)的图象与x轴有交点⇔函数y＝f(x)有零点．‎ ‎3．零点存在性定理 如果函数y＝f(x)满足：①在区间[a，b]上的图象是连续不断的一条曲线；②f(a)·f(b)<0；则函数y＝f(x)在(a，b)上存在零点，即存在c∈(a，b)，使得f(c)＝0，这个c也就是方程f(x)＝0的根．‎ ‎(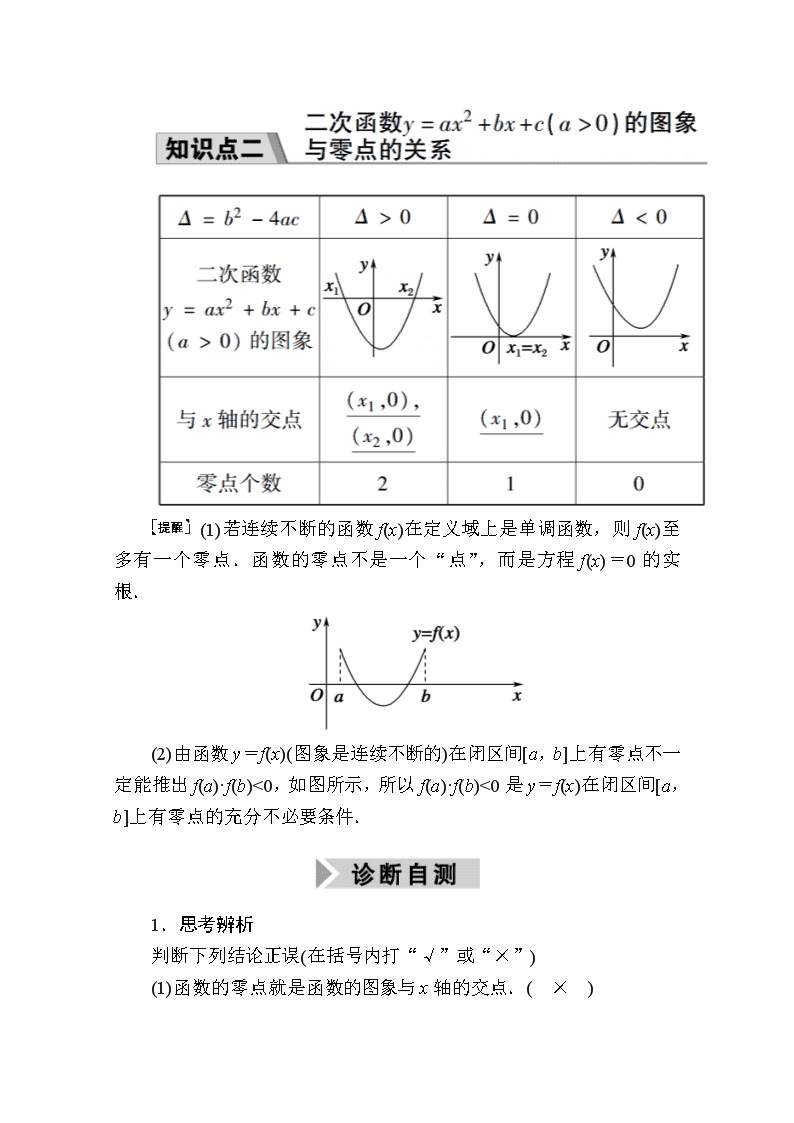1)若连续不断的函数f(x)在定义域上是单调函数，则f(x)至多有一个零点．函数的零点不是一个“点”，而是方程f(x)＝0的实根．‎ ‎(2)由函数y＝f(x)(图象是连续不断的)在闭区间[a，b]上有零点不一定能推出f(a)·f(b)<0，如图所示，所以f(a)·f(b)<0是y＝f(x)在闭区间[a，b]上有零点的充分不必要条件．‎ ‎1．思考辨析 判断下列结论正误(在括号内打“√”或“×”)‎ ‎(1)函数的零点就是函数的图象与x轴的交点．(　×　)‎ ‎(2)函数y＝f(x)在区间(a，b)内有零点(函数图象连续不断)，则f(a)·f(b)<0.(　×　)‎ ‎(3)二次函数y＝ax2＋bx＋c(a≠0)在b2－‎4ac<0时没有零点．(　√　)‎ ‎2．小题热身 ‎(1)已知函数f(x)的图象是连续不断的，且有如下对应值表：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ f(x)‎ ‎－4‎ ‎－2‎ ‎1‎ ‎4‎ ‎7‎ 在下列区间中，函数f(x)必有零点的区间为(　B　)‎ A．(1,2) B．(2,3)‎ C．(3,4) D．(4,5)‎ 解析：由所给的函数值的表格可以看出，x＝2与x＝3这两个数字对应的函数值的符号不同，即f(2)·f(3)<0，所以函数f(x)在(2,3)内有零点．‎ ‎(2)若函数f(x)唯一的零点同时在区间(0,16)，(0,8)，(0,4)，(0,2)内，那么下列命题正确的是(　C　)‎ A．函数f(x)在区间(0,1)内有零点 B．函数f(x)在区间(0,1)或(1,2)内有零点 C．函数f(x)在区间[2,16)上无零点 D．函数f(x)在区间(1,16)内无零点 解析：由题意可确定f(x)唯一的零点在区间(0,2)内，故在区间[2,16)内无零点．‎ ‎(3)(2020·济南月考)若函数f(x)＝x2＋2x＋a没有零点，则实数a的取值范围是(　B　)‎ A．(－∞，1) B．(1，＋∞)‎ C．(－∞，1] D．[1，＋∞)‎ 解析：因为函数f(x)＝x2＋2x＋a没有零点，所以方程x2＋2x＋a＝0无实根，即Δ＝4－‎4a<0，由此可得a>1.‎ ‎(4)函数f(x)＝cos在[0，π]的零点个数是3.‎ 解析：由题意知，cos＝0，所以3x＋＝＋kπ，k∈Z，所以x＝＋，k∈Z，当k＝0时，x＝；当k＝1时，x＝；当k＝2时，x＝，均满足题意，所以函数f(x)在[0，π]的零点个数为3.‎ ‎(5)(2020·西安调研)若方程2x＋3x＝k的解在[1,2)内，则k的取值范围是[5,10)．‎ 解析：令函数f(x)＝2x＋3x－k，则f(x)在R上是增函数．当方程2x＋3x＝k的解在(1,2)内时，f(1)·f(2)<0，即(5－k)(10－k)<0，解得51,00，∴f(x)在区间(－1,0)上存在零点．故选B.‎ ‎(2)令g(x)＝x，f(x)＝x，则g(0)＝1>f(0)＝0，g＝f＝，结合图象可得0，所以f(2)f(3)<0，所以函数的零点所在的区间是(2,3)．‎ ‎2．已知函数f(x)＝logax＋x－b(a>0且a≠1)．当21，在同一坐标系中画出函数y＝logax，y＝－x＋b的图象，判断两个函数图象的交点的横坐标在(2,3)内，∴函数f(x)的零点x0∈(n，n ‎＋1)时，n＝2.‎ 考点二　函数零点个数的判断 ‎【例2】　(1)函数f(x)＝的零点个数是________．‎ ‎(2) (2020·衡水中学模拟)定义在R上的函数f(x)满足f(x)＝且f(x＋1)＝f(x－1)，若g(x)＝3－log2x，则函数F(x)＝f(x)－g(x)在(0，＋∞)内的零点个数为(　　)‎ A．3　　　　 B．2 ‎ C．1　　　　 D．0‎ ‎【解析】　(1)当x≤0时，令x2－2＝0，解得x＝－(正根舍去)，所以在(－∞，0]上，f(x)有一个零点；当x>0时，f′(x)＝2＋>0恒成立，所以f(x)在(0，＋∞)上是增函数．又因为f(2)＝－2＋ln2<0，f(3)＝ln3>0，所以f(x)在(0，＋∞)上有一个零点，综上，函数f(x)的零点个数为2.‎ ‎(2)由f(x＋1)＝f(x－1)知f(x)的周期是2，画出函数f(x)和g(x)的部分图象，如图所示，由图象可知f(x)与g(x)的图象有2个交点，故F(x)在(0，＋∞)内有2个零点．故选B.‎ ‎【答案】　(1)2　(2)B 方法技巧 函数零点个数的判断方法 (1)直接求零点.‎ (2)利用零点存在性定理再结合函数的单调性确定零点个数.‎ (3)利用函数图象的交点个数判断.‎ ‎1．已知函数f(x)＝则函数g(x)＝f(1－x)－1的零点个数为(　C　)‎ A．1 B．2‎ C．3 D．4‎ 解析：g(x)＝f(1－x)－1‎ ‎＝ ‎＝ 易知当x≥1时，函数g(x)有1个零点；当x<1时，函数g(x)有2个零点，所以函数g(x)的零点共有3个，故选C.‎ ‎2．函数f(x)＝－cosx在[0，＋∞)内(　B　)‎ A．没有零点 B．有且仅有一个零点 C．有且仅有两个零点 D．有无穷多个零点 解析：当x∈(0,1]时，因为f′(x)＝＋sinx，>0，sinx>0，所以f′(x)>0，故f(x)在[0,1]上单调递增，且f(0)＝－1<0，f ‎(1)＝1－cos1>0，所以f(x)在[0,1]内有唯一零点．当x>1时，f(x)＝－cosx>0，故函数f(x)在[0，＋∞)上有且仅有一个零点，故选B.‎ 考点三　由函数的零点求参数的取值范围 ‎【例3】　(1)若函数f(x)＝－ln(x＋1)不存在零点，则实数k的取值范围是________．‎ ‎(2)若函数f(x)＝(m－2)x2＋mx＋‎2m＋1的两个零点分别在区间(－1,0)和区间(1,2)内，则m的取值范围是________．‎ ‎【解析】　(1)当k＝0时，f(x)没有意义；‎ 当k<0时，f(x)＝lnkx－ln(x＋1)的定义域为(－1,0)，此时f(x)＝lnkx－ln(x＋1)＝0⇔ 令g(x)＝x2＋(2－k)x＋1，则g(－1)＝k<0，g(0)＝1>0，由存在性定理知，函数g(x)在区间(－1,0)内有根，即f(x)存在零点，不符合题意；‎ 当k>0时，函数f(x)的定义域为(0，＋∞)，‎ 此时f(x)＝lnk＋lnx－ln(x＋1)，‎ 令f′(x)＝－＝0，解得x＝1.‎ 当00，当x>1时，f′(x)<0，‎ 所以f(x)在x＝1处取得最大值，‎ 当且仅当f(1)<0时，f(x)不存在零点，‎ 即f(1)＝lnk－ln2<0，‎ 解得01时，有交点，即函数g(x)＝f(x)＋x－m有零点．‎ ‎2．已知函数f(x)＝2mx2－x－1在区间(－2,2)上恰有一个零点，则m的取值范围是(　D　)‎ A. B. C. D. 解析：当m＝0时，函数f(x)＝－x－1有一个零点x＝－1，满足条件．当m≠0时，函数f(x)＝2mx2－x－1在区间(－2，2)内恰有一个零点，需满足①f(－2)·f(2)<0或②或③ 解①得－0 B．b>0，c>0‎ C．b<0，c＝0 D．b≥0，c＝0‎ ‎【解析】　设f(x)＝t，则方程化为t2＋bt＋c＝0.①‎ 作出函数f(x)的图象如图所示．‎ 由图知，当t<0时，1个t对应0个x；‎ 当t＝0时，1个t对应3个x；‎ 当t>0时，1个t对应4个x.‎ 因此，要使原方程有7个不同的实数解，①的一个根为0，一个根为正数，故c＝0.所以①的两根为t1＝0，t2＝－b>0，所以b<0.故选C.‎ ‎【答案】　C ‎【素养解读】　换元法是解方程的重要方法，本例利用换元法，设f(x)＝t，则方程化为t2＋bt＋c＝0，将问题转化为关于t的一元二次方程的根的分布问题．‎ 已知f(x)＝|ex－1|＋1，若函数g(x)＝[f(x)]2＋(a－2)f(x)－‎2a有三个零点，则实数a的取值范围是(　A　)‎ A．(－2，－1) B．(－1,0)‎ C．(0,1) D．(1,2)‎ 解析：令t＝f(x)，则函数g(x)＝t2＋(a－2)t－‎2a，由t2＋(a－2)t－‎2a＝0，得t＝2或t＝－a.f(x)＝|ex－1|＋1＝作出函数f(x)的图象，如图所示，由图可知当t＝2时，方程f(x)＝|ex－1|＋1＝2有且仅有一个根，则方程f(x)＝|ex－1|＋1＝－a必有两个不同的实根，此时由图可知1<－a<2，即－2