湖北省天门市、仙桃市、潜江市2018-2019学年高一下学期期末考试数学试题 Word版含答案 8页

www.ks5u.com 天门 仙桃 潜江 ‎ 2018~2019学年度第二学期期末联考试题 高 一 数 学 本试卷共4页，全卷满分150分，考试时间120分钟。‎ ‎★祝考试顺利★‎ 注意事项：‎ ‎1、考生在答题前，请务必将自己的姓名、准考证号等信息填在答题卡上。‎ ‎2、选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试卷上无效。‎ ‎3、填空题和解答题用0.5毫米黑色签字笔答在答题卡上每题对应的答题区域内。答在试卷上无效。‎ 一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．集合，集合，集合，则集合的真子集有 A．2个 B．3个 C．4个 D．8个 ‎2．设复数满足,则 A． B．‎5 ‎ C． D． ‎ ‎3．甲乙两名同学近几次信息技术比赛(满分为26分)得分统计成绩茎叶图如图，若甲乙比赛成绩的平均数与中位数分别相等，则有序数对（x，y）为 ‎ A．（3，2） B．（2，3） ‎ C．（3，1）或（7，5） D．（3，2）或（7，5） ‎ ‎4．若对任意正数x，不等式恒成立，则实数a的最大值为 A．1 B． C． D．‎ ‎5．若向量，，且，则 A．2 B． C．7 D．‎ ‎6．若l，m是平面外的两条不同的直线，且，则“”是“”的 A．充分而不必要条件 B．必要而不充分条件 ‎ C．充分必要条件 D．既不充分也不必要条件 ‎ ‎7．某人打开手机时，忘记了开机的六位密码的第二位和第四位，只记得第二位是7,8,9‎ - 8 -‎ 中的一个数字，第四位是1,2,3中的一个数字，则他输入一次能够开机的概率是 A． B． C． D． ‎ ‎8．已知函数，若将的图象向左平移个单位后所得函数的图象关于轴对称，则 A． B． C． D． ‎ ‎9．一个四面体共一个顶点的三条棱两两垂直，其长分别为1，，3，且四面体的四个顶点在同一球面上，则这个球的体积为 A． B． C． D．‎ ‎10．已知奇函数是上的减函数，，，，则 A． B． C． D． ‎ ‎11．如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为，，此时气球的高度是，则河流的宽度BC等于 ‎ A．m B．m ‎ C．m D．m ‎12．对任意实数a，b定义运算“”；，‎ 设，若函数至少有两个零点，则k的取值范围是 ‎ A． B． C． D．‎ 二、填空题（本大题共4小题，每小题5分，共20分．把答案填在答题卡上对应题号后的横线上）‎ ‎13．某校对全校男女学生共1600名进行健康调查，选用分层抽样法抽取一个容量为200的样本．已知男生比女生多抽了10人，则该校的男生人数应是 ▲ 人． ‎ ‎14．在中，a，b，c分别为三内角A，B，C所对的边，设向量，，若，则角A的大小为 ▲ ． ‎ - 8 -‎ ‎15．某城市有甲、乙两种报纸供市民订阅，记事件A为“只订甲报纸”，事件B为“至少订一种报纸”，事件C为 “至多订一种报纸”，事件D为“不订甲报纸”，事件E为“一种报纸也不订”．下列命题正确的是 ▲ ．‎ ‎ ①A与C是互斥事件 ②B与E 是互斥事件，且是对立事件 ‎ ‎③B与C不是互斥事件 ④C与E是互斥事件 ‎16．已知函数 ．若，使，则实数m的取值范围是 ▲ ． ‎ 三、解答题（本大题共6个小题，共70分．解答应写出文字说明，证明过程或演算步骤）‎ ‎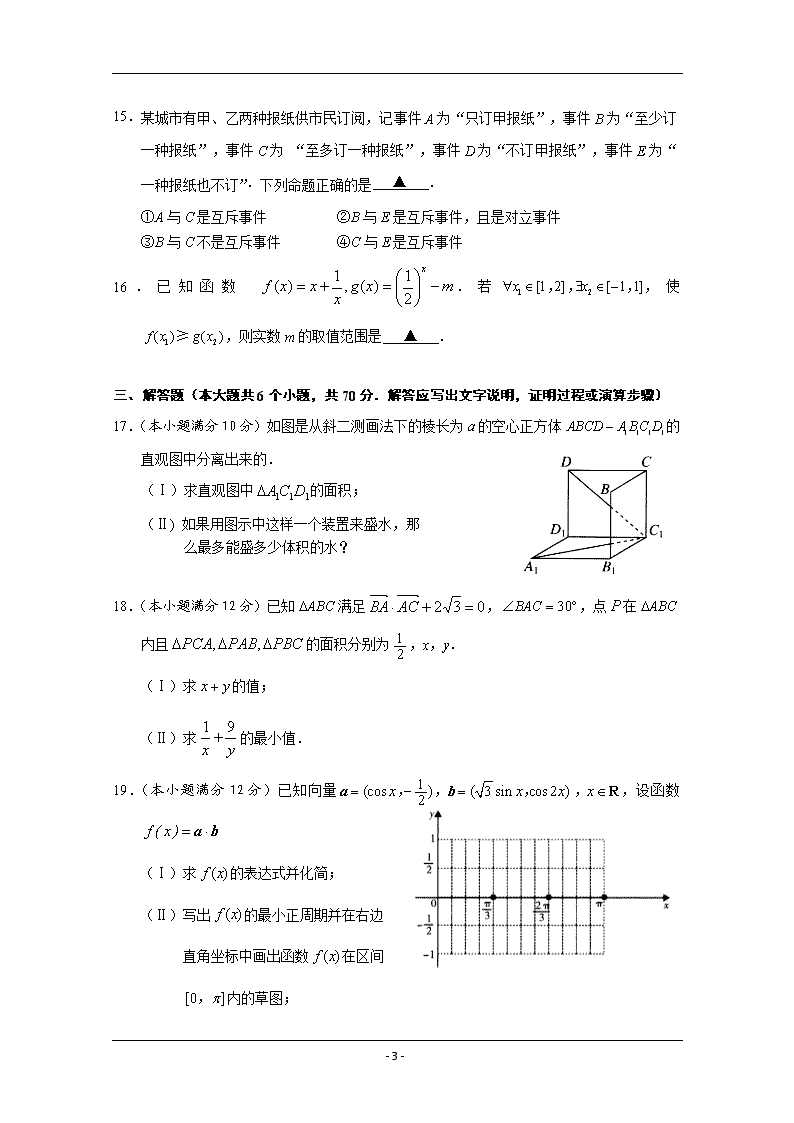17．（本小题满分10分）如图是从斜二测画法下的棱长为a的空心正方体的直观图中分离出来的．‎ ‎（Ⅰ）求直观图中的面积；‎ ‎（Ⅱ) 如果用图示中这样一个装置来盛水，那 么最多能盛多少体积的水？‎ ‎18．（本小题满分12分）已知满足，，点在内且的面积分别为，x，y．‎ ‎ （Ⅰ）求的值；‎ ‎ （Ⅱ）求的最小值．‎ ‎19．（本小题满分12分）已知向量，设函数 ‎ ‎（Ⅰ）求的表达式并化简；‎ ‎（Ⅱ）写出的最小正周期并在右边 直角坐标中画出函数在区间 内的草图；‎ - 8 -‎ ‎（Ⅲ）若方程在上有 两个根，求m的取值范围及的值．‎ ‎20．（本小题满分12分）两个同乡大学生携手回乡创业，他们引进某种果树在家乡进行种植试验．他们分别在五种不同的试验田中种植了这种果树100株并记录了五种不同的试验田中果树的死亡数，得到如下数据：‎ 试验田 试验田1‎ 试验田2‎ 试验田3‎ 试验田4‎ 试验田5‎ 死亡数 ‎23‎ ‎32‎ ‎24‎ ‎29‎ ‎17‎ ‎（Ⅰ）求这五种不同的试验田中果树的平均死亡数；‎ ‎ （Ⅱ）从五种不同的试验田中随机取两种试验田的果树死亡数，记为x，y，用（x，y）的形式列出所有的基本事件，其中（x，y）和（y，x）视为同一事件，并求的概率．‎ ‎21．（本小题满分12分）如图，在底面为平行四边形的四棱锥 中，过点的三条棱PA、AB、AD两两垂直且 相等，E，F分别是AC，PB的中点．‎ ‎（Ⅰ）证明：EF//平面PCD；‎ ‎ （Ⅱ）求EF与平面PAC所成角的大小．‎ ‎22．（本小题满分12分）已知，函数满足．‎ ‎（Ⅰ）当时，解不等式；‎ ‎ （Ⅱ）若关于x的方程的解集中有且只有一个元素，求a的值；‎ ‎ （Ⅲ）设，若对，函数在区间上的最大值与最小值的差不超过1，求a的取值范围．‎ - 8 -‎ 天门 仙桃 潜江 ‎ 2018~2019学年度第二学期期末联考试题 高一数学参考答案 一、选择题（本大题共12小题，每小题5分，共60分．）‎ ‎1．B 2．B 3．A 4．C 5．C 6．C 7．C 8．B 9．B 10．D 11．B 12．A 二、填空题（本大题共4小题，每小题5分，共20分．）‎ ‎13． 840‎ ‎14． 或写成 ‎15．②③ ‎ ‎16． ‎ 三、解答题（本大题共6个小题，共70分．）‎ ‎17．解：（Ⅰ）…………5分 ‎ （Ⅱ）如果用图示中的装置来盛水，那么最多能盛的水的体积等于三棱锥的体积，所以……………………………………10分 ‎18．解：（Ⅰ）由已知得，得………………………3分 ‎ 故 ‎ 又，则………………………………………………6分 ‎ （Ⅱ）‎ ‎ …………………………………………12分 ‎19．解：（Ⅰ） ………………………………4分 ‎（Ⅱ）的最小正周期……………………………………………………5分 - 8 -‎ ‎……………8分 ‎（Ⅲ）由图可知，当时，，即 当时， ，即 ‎ ∴…………………………………………………………12分 ‎20．解：（Ⅰ）由题意，这5种试验田果树的的平均死亡数为：‎ ‎……………………………………………………2分 ‎ （Ⅱ）（x，y）的取值情况有：（23，32），（23，24），（23，29），（23，17），（32，24），（32，29），（32，17），（24，29），（24，17），（29，17）…………………4分 ‎ 基本事件总数n=10………………………………………………………………5分 设满足的事件为A，则事件A包含的基本事件为：‎ ‎（23，32），（32，17），（29，17），共有m=3个， ∴…………8分 设满足的事件为B，则事件B包含的基本事件为：‎ ‎（23，24），（32，29），共有个， ∴……………………10分 ‎∴的概率…………12分 ‎21．（Ⅰ）证明：如图，连接BD，则E是BD的中点 ‎ 又F是PB的中点，‎ ‎ ∴ EF//PD……………………………………3分 ‎ ∵ EF不在平面PCD内，‎ ‎ ∴ EF//平面PCD………………………………………………………6分 ‎ （Ⅱ）解：连接PE，‎ ‎∵ ABCD是正方形，∴‎ - 8 -‎ 又平面，∴‎ ‎∴平面，故是PD与平面PAC所成的角……………9分 ‎∵EF//PD，∴EF与平面PAC所成的角的大小等于 ‎∵PA=AB=AD，，‎ ‎∴≌，因此PD=BD ‎ 在中，，‎ ‎ ∴EF与平面PAC所成角的大小是……………………………………12分 ‎22．解：（Ⅰ）由题意可得，得，解得…………2分 ‎ （Ⅱ）方程有且仅有一解， 等价于有且仅有一解，且 ………………4分 ‎ 当时，符合题意；‎ ‎ 当时，此时满足题意 ‎ ‎ 综上，或…………………………………………………………6分 ‎ （Ⅲ）当时，，‎ ‎ 所以在上单调递减 ‎ 函数在区间上的最大值与最小值分别为，，‎ ‎ ‎ ‎ 即对任意恒成立……………………………8分 ‎ 因为， 所以函数在区间上单调递增，‎ ‎ 所以时，y有最小值，‎ - 8 -‎ ‎ 由，得 ‎ 故a的取值范围为………………………………………………12分 - 8 -‎