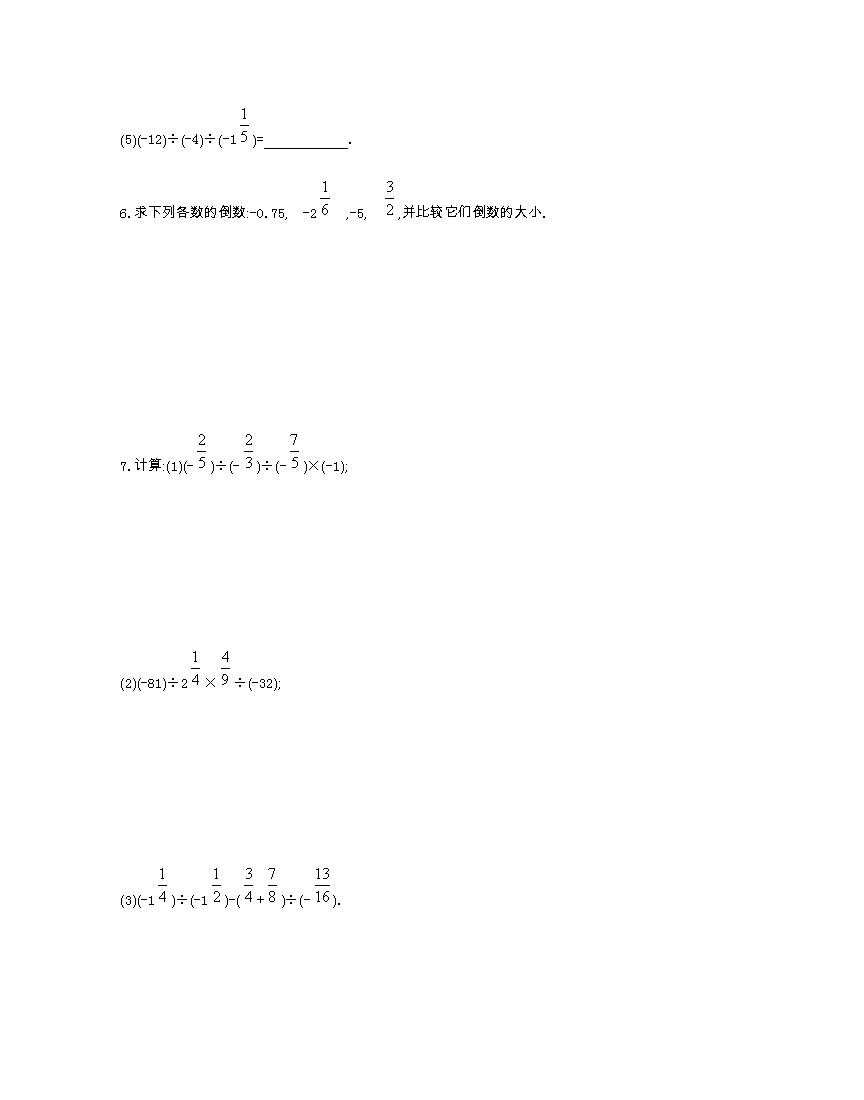北师七年级数学上册 第二章六节 同步课时检测卷(附参考答案） 16页

北师七上数学测试题第二章六节 ‎1.两个有理数相除(除数不为零),同号得　　　　　,异号得　　　　　,并把绝对值　　　　　　.除以一个数(除数不能为0)等于乘这个数的　　　　　　.0除以任何非0的数都得　　　　　.‎ ‎2.(1)(-10)÷5=　　　　　　;‎ ‎(2)(-8)÷(-2)=　　　　　　;‎ ‎(3)(-)÷(-)=　　　　　　.‎ ‎3.下列说法中正确的是(　　)‎ A.0除以任何数都得0‎ B.有理数的商必小于被除数 C.互为相反数的两数的积为负数 D.0没有倒数 ‎4.用“<”“>”或“=”填空。‎ ‎(1)(-)÷(-)÷(-)　　　　　0;‎ ‎(2)(-)÷÷(-)　　　　　0;‎ ‎(3)0÷(-5)÷(-7)　　　　　0.‎ ‎5.计算:(1)(-9)÷3=　　　　　　;‎ ‎(2)-24÷0.6=　　　　　　;‎ ‎(3)1÷(-1)=　　　　　　;‎ ‎(4)÷(-)=　　　　　　　;‎ ‎(5)(-12)÷(-4)÷(-1)=　　　　　　.‎ ‎6.求下列各数的倒数:-0.75,　-2　,-5,　,并比较它们倒数的大小.‎ ‎7.计算:(1)(-)÷(-)÷(-)×(-1);‎ ‎(2)(-81)÷2×÷(-32);‎ ‎(3)(-1)÷(-1)-(+)÷(-).‎ ‎8.已知海拔每升高1 000 m,气温下降6 ℃,某人乘热气球旅行,在地面时测得温度是8 ℃,当热气球升空后,测得高空温度是-1 ℃,求热气球的高度.‎ ‎9.数学老师布置了一道思考题“计算:(-)÷( - )”,小明仔细思考了一番,用了一种与众不同的方法解决了这个问题.‎ 小明的解法:原式的倒数为(- )÷(-)=( - )×(-12)=-4+10=6,‎ 所以(-)÷( - )=.‎ ‎(1)请你判断小明的解答是否正确,并说明理由;‎ ‎(2)请运用小明的解法解答下面的问题.‎ 计算:(-)÷( - +).‎ ‎10.下列计算正确的是(　　)‎ A.2÷(-3.5)=7‎ B.(-3)÷(-6)=2‎ C.1÷(-)=-4.5‎ D.(-1)÷2=-1‎ ‎11.计算-27÷3×的结果是(　　)‎ A.-27‎ B.27‎ C.-3‎ D.3‎ ‎12.实数a,b在数轴上对应点的位置如图2-8-1所示,则必有(　　)‎ ‎　　　　　　　　　　‎ ‎　　　　　　　　　　　　　　　图2-8-1‎ A.a+b>0‎ B.a-b<0‎ C.ab>0‎ D.<0‎ ‎13.计算:(1)3×(3-7)×‎ ‎(2)÷(-2)-×(-1)-‎ ‎(3)0-7÷|-12|××9÷(-)‎ ‎(4)(-3)÷(-1)×3‎ ‎(5)(-8)÷[(-)÷(-)]÷(-2)‎ ‎14.如果a,b互为相反数,x,y互为倒数,则(a+b)×-xy的值是多少?‎ ‎15.某冷冻厂的一个冷库的室温是-4 ℃,现有一批食品需要在-28 ℃冷藏,如果每小时降低3 ℃,则经过多少小时能降到所要求的温度?‎ ‎16.一天,甲,乙两人利用温差测量山峰的高度,甲在山顶测得温度是-1 ℃,乙此时在山脚测得温度是5 ℃,已知该地区高度每增加100米,气温大约降低0.6 ℃,这个山峰的高度大约是多少米?‎ ‎17.小华在课外书中看到这样一道题:‎ 计算:÷( + - - )+( + - - )÷.‎ 她发现,这个算式反映的是前后两部分的和,而这两部分之间存在着某种关系,利用这种关系,她顺利地解答了这道题.‎ ‎(1)前后两部分之间存在着什么关系?‎ ‎(2)先计算哪部分比较简便?并请计算比较简便的那部分;‎ ‎(3)利用(1)中的关系,直接写出另一部分的结果;‎ ‎(4)根据以上分析,求出原式的结果.‎ ‎18.求n个相同的因数a的　　　的运算叫做乘方,记作　　　.乘方的结果叫做　　　,a叫做　　　　,n叫做　　　　　　,an读作　　　　　　　(或　　　　　　　). ‎ ‎19.正数的任何次幂都是　　　　　　.负数的奇次幂是　　　　　　,负数的偶次幂是　　　　　　.‎ ‎20.(1)在()4中,底数是　　　　　,指数是　　　　　　;‎ ‎(2)在-32中,底数是　　　　　　,指数是　　　　　　;‎ ‎(3)在(-2)3中,底数是　　　　　　,指数是　　　　　　.‎ ‎21.(-4)·(-4)·(-4)·(-4)·(-4)表示成幂的形式为　　　　　　　　.‎ ‎22.计算:(1)-12‎ ‎(2)(-3)2‎ ‎(3)(-)3.‎ ‎23.下列关于(-3)4的说法正确的是(　　)‎ A.-3是底数,4是幂 B.-3是底数,4是指数,-12是幂 C.3是底数,4是指数,81是幂 D.-3是底数,4是指数,81是幂 ‎24.下列各式计算正确的是(　　)‎ A.-24=-8‎ B.-(-2)2=-4‎ C.(-)3=-1‎ D.(-2)3=8‎ ‎25.下列各组数中,其值相等的是(　　)‎ A.32和23‎ B.(-2)3和-23‎ C.-32和(-3)2‎ D.(-3×2)2和(-3×22)‎ ‎26.(-)·(-)·(-)写成幂的形式为　　　　　　.‎ ‎27.计算:‎ ‎(1)(-5)4‎ ‎(2)-54‎ ‎(3)(-)3;(4)(-1)101‎ ‎(5)(1)3;(6)(-2)2 017+22 017‎ ‎28.计算(-1)2 017的结果为(　　)‎ A.2 017‎ B.-2 017‎ C.1‎ D.-1‎ ‎29.下列各式中,正确的是(　　)‎ A.32=(-3)2‎ B.33=(-3)3‎ C.-34=|-34|‎ D.(-5)3=|(-5)3|‎ ‎30.下列各式:①-(-3);②-|-3|;③(-3)2;④-32;⑤-(-3)4;⑥-(-3)3,其中结果为负数的是　　　　.(填序号) ‎ ‎31.在-中,底数是　　　　　　,指数是　　　　　　.‎ ‎32.一个数的平方是36,则这个数是　　　　　　;一个数的立方是-27,则这个数是　　　　　　.‎ ‎33.一根1 m长的绳子,第1次剪去全长的,第2次剪去剩下的,如此剪下去,则第6次后剩下的绳子长为　　　　　　　.‎ ‎34.若|a-1|+(b+2)2=0,求(a+b)2 017+a2 016的值.‎ ‎35.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,….‎ 通过观察,能用你所发现的规律写出232的个位数字是多少吗?能写出32 015的个位数字吗?‎ ‎36.为了计算1+2+22+23+…+210的值,我们采用如下方法:‎ 设S=1+2+22+23+24+…+29+210①,‎ 则2S=2+22+23+24+…+29+210+211②,‎ 由②-①,得S=211-1.‎ 利用上述方法,求1+5+52+53+54+…+52 014+52 015的值.‎ 参考答案 ‎1.正　　　负　　　相除　　　倒数　　　0‎ ‎2.(1)-2‎ ‎(2)4‎ ‎(3)2‎ ‎3.D ‎4.(1)<‎ ‎(2)>‎ ‎(3)=‎ ‎5.(1)-3‎ ‎(2)-40‎ ‎(3)-‎ ‎(4)-‎ ‎(5)-‎ ‎6.解:因为-0.75的倒数为-,-2的倒数为-,-5的倒数为-,的倒数为,‎ 所以- < - < - < .‎ ‎7.(1)‎ ‎(2)‎ ‎(3)2‎ ‎8.解:根据题意得:[8-(-1)]÷6×1000=1500(m),‎ 即热气球的高度为1500 m.‎ ‎9.(1)解:正确,理由为:一个数的倒数的倒数等于原数;‎ ‎(2)解:原式的倒数为( - + )÷(- )‎ ‎=( - + )×(-24)‎ ‎=-8+4-9‎ ‎=-13,‎ 则(-)÷( - + )=-.‎ ‎10.C ‎11.C ‎12.D ‎13.(1)-4‎ ‎(2)‎ ‎(3)4‎ ‎(4)‎ ‎(5)3‎ ‎14.解:由题意,得a+b=0,xy=1,‎ 所以(a+b)×-xy ‎=0×-1‎ ‎=-1.‎ ‎15.[-4-(-28)]÷3=8(小时).‎ ‎16.解:由题意,得100×{[5-(-1)]÷0.6}=100×(6÷0.6)=1000(米).‎ 答:这个山峰的高度大约是1000米.‎ ‎17.(1)解:前后两部分互为倒数;‎ ‎(2)解:先计算后一部分比较简便.‎ ‎( + - - )÷‎ ‎=( + - - )×36‎ ‎=9+3-14-1‎ ‎=-3.‎ ‎(3)解:因为前后两部分互为倒数,‎ 所以 ÷ ( + - - )= - .‎ ‎(4)解:根据以上分析,可知原式=-+(-3)=-3.‎ ‎18.积　　　an　　　幂　　　底数　　　指数　　　a的n次幂　　　a的n次方 ‎19.正数　　　负数　　　正数 ‎20.(1)　　　4‎ ‎(2)3　　　2‎ ‎(3)-2　　　3‎ ‎21.(-4)5‎ ‎22.(1)-12=-1‎ ‎(2)(-3)2=9‎ ‎(3)(-)3=- ‎ ‎23.D ‎24.B ‎25.B ‎26.(- )3‎ ‎27.(1)625‎ ‎(2)-625‎ ‎(3)- ‎ ‎(4)-1‎ ‎(5)　　　0‎ ‎28.D ‎29.A ‎30.②④⑤‎ ‎31.2　　　3‎ ‎32.±6　　　-3‎ ‎33. m ‎34.解:由题意,得a=1,b=-2,‎ 所以原式=(1-2)2 017+12 016=0.‎ ‎35.解:可以看出这些幂的个位数字呈周期性出现,2,4,8,6,…,每4个为一个周期,32÷4=8,所以可推知,232的个位数字是6.‎ 而31=3,32=9,33=27,34=81,35=243,36=729,37=2 187,38=6 561,…,因2 015÷4=503余3,因此32 015的个位数字是7.‎ ‎36.解:令S=1+5+52+53+54+…+52014+52015‎ 则5S=5+52+53+54+…+52015+52016,‎ 所以5S-S=52016-1,‎ 所以S=.‎