七年级上数学课件- 1-4-1 有 理 数 的 乘 法 课件（共39张PPT）_人教新课标 39页

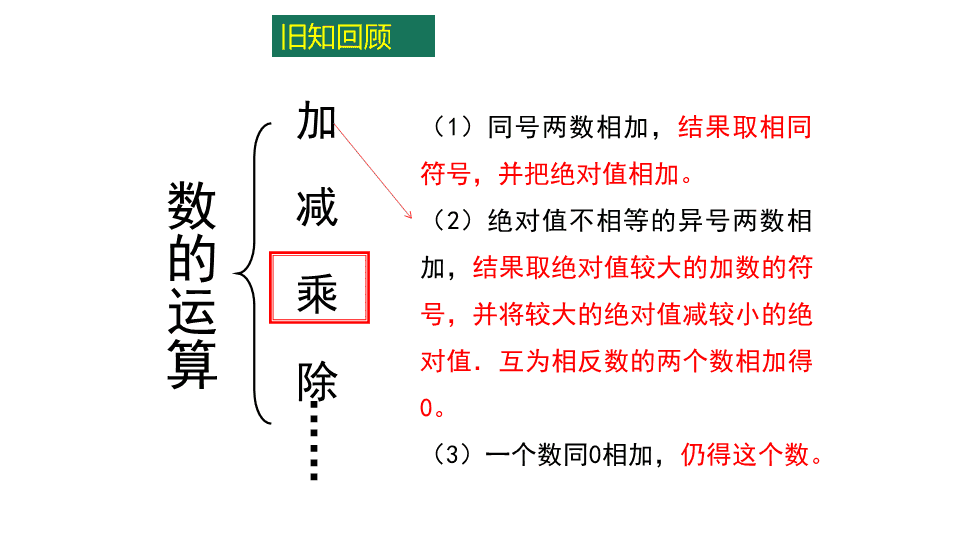
有理数的乘法第一课时 旧知回顾数的运算加减乘除……（1）同号两数相加，结果取相同符号，并把绝对值相加。（2）绝对值不相等的异号两数相加，结果取绝对值较大的加数的符号，并将较大的绝对值减较小的绝对值．互为相反数的两个数相加得0。（3）一个数同0相加，仍得这个数。 同学们，请你计算（+2）+（+2）+（+2）=；问题探究（-2）+（-2）+（-2）=。6-6能否将上述加法运算改写成乘法运算的形式？改写（+2）×（+3）=6（-2）×（+3）=-6①②从①②式中你可以得到什么结论？两数相乘，若把一个因数换成它的相反数，则所得的积是原来积的相反数。问题1 请你再计算“（+2）×（-3）和（-2）×（-3）”并说明理由。新知探究因为（+2）×（+3）=6，所以（+2）×（-3）=-6。问题2（+2）×（-3）=-6两数相乘，若把一个因数换成它的相反数，则所得的积是原来积的相反数。（-2）×（-3）=+6因为（-2）×（+3）=-6，所以（-2）×（-3）=+6。③④ 新知探究问题2观察式子①~④，你又可得到什么结论？（+2）×（+3）=6（-2）×（+3）=-6①②（+2）×（-3）=-6（-2）×（-3）=+6③④由①④得，同号两数相乘得正，并把绝对值相乘。由②③得，异号两数相乘得负，并把绝对值相乘。 新知探究你能概括出有理数乘法的规则吗？问题3计算0×（-3）=，为什么？0因为0×3=0，所以0×（-3）=0。两数相乘，同号得正，异号得负，并把绝对值相乘；任何数与零相乘都得零。 负负得正---生活缩影话题1朋友的朋友是朋友（正正得正）；朋友的敌人是敌人（正负得负）；敌人的朋友是敌人（负正得负）；敌人的敌人是朋友（负负得正）。话题2好人有好报是好事（正正得正）；好人有坏报是坏事（正负得负）；坏人有好报是坏事（负正得负）；坏人有坏报是好事（负负得正）。 新知应用趁热打铁例1、计算：(1)9×6；(2)(-9)×6；(3)3×（-4）；(4)（-3）×（-4）。解：(1)9×6=+(9×6)=54；(3)3×（-4）=-（3×4）=-12①确定积的符号②绝对值相乘(2)(-9)×6=-(9×6)=-54；(4)（-3）×（-4）=+（3×4）=12 新知应用趁热打铁例2、计算：在乘法计算时，遇到带分数，应先化为假分数；遇到小数，应先化成分数，再进行计算。 新知应用问题3请你计算？？解：观察上面两题有何特点？总结：有理数中仍然有：乘积是1的两个数互为倒数。数a(a≠0)的倒数是什么？(a≠0时，a的倒数是)强调：0没有倒数 新知应用１，－１，，，8，－9，，－2.5趁热打铁原数1－18－9－2.5倒数解：1－14例3、说出下列各数的倒数 新知应用趁热打铁例4、用正负数表示气温的变化量，上升为正，下降为负，登山队攀登一座山峰，每登高1km，气温的变化量为-6℃，向上攀登3km后，气温有什么变化？hkm(h+3)km解：(1)(-6)×3=-18答：气温下降18℃。（2）（-6）×（-3）=18答：气温上升18℃，此时登山队回到原出发点。继续向上攀登-3km之后，气温又如何变化？此时登山队位于何处？ 梳理反思确定类型定符号绝对值同号异号互为倒数相乘与0相乘有理数的乘法法则：＋﹣相乘相乘结果是0结果是1 有理数的乘法第二课时 旧知回顾有理数乘法法则（1）两数相乘，同号，异号，并把相乘；（2）任何数与零相乘都得。（3）乘积是1的两个数。 同学们，将下列数字填到九宫格里，使得九宫格的横竖和对角线上数字的乘积都是负数。问题引入学习本节课内容后，轻而易举你就会！思考2，3，4，-2，-3，-4，5，6，7多个有理数相乘 新知探究问题1观察下列各式，它们的积是正的还是负的？2×3×4×(-5)=，2×3×(-4)×(-5)=，2×(-3)×(-4)×(-5)=，(-2)×(-3)×(-4)×(-5)=。-120+120-120+120【思考】几个不是0的数相乘，积的符号与负因数的个数之间有什么关系？ 新知探究归纳经过观察，可得到什么结论？几个不是0的数相乘，负因数的个数是偶数时，积是正数；负因数的个数是奇数时，积是负数。“奇负偶正”定号算值“积的绝对值” 新知应用趁热打铁例1、计算：与两个有理数相乘的计算方法相比较，思考多个不是0的数相乘，先做哪一步，再做哪一步？ 新知探究问题2你能看出下式的结果吗？如果能，请说明理由。？几个数相乘，如果其中有因数为0，那么积等于0。0无论多复杂 新知应用趁热打铁例2、计算： 同学们，将下列数字填到九宫格里，使得九宫格的横竖线和对角线上数字的乘积都是负数。新知应用解决2，3，4，-2，-3，-4，5，6，7展示一下你是如何填的？-2-3-4234567 梳理反思多个有理数的乘法法则几个不是0的数相乘，负因数的个数是偶数时，积是正数；负因数的个数是奇数时，积是负数。几个数相乘，如果其中有因数为0，那么积等于0。 判断下列式子乘积的符号：（1）-6×0.35×(-1.56)×20×2018；（2）101×25×(-0.7)×(-10)×(-5.9)；（3）21×(-8)×(1.23)×(-4)×(-81)；（4）23×67.3×(-2.47)×0×3.4。课后练习 有理数的乘法第三课时 问题引入1.有理数的乘法法则是什么？两数相乘，同号得正，异号得负，并把绝对值相乘。任何数和零相乘，都得0。2.如何进行多个有理数的乘法运算？（1）定号（奇负偶正）（2）算值（积的绝对值）3.小学大家学过乘法的哪些运算律？乘法交换律、乘法结合律、乘法分配律。 新知探究探究1观察下列各式，它们的积是正的还是负的？【思考】上面每小组分别体现了什么运算律？（2）（3×4）×0.25=3×（4×0.25）=，（1）2×3=3×2=，（3）2×(3+4)=2×3+2×4=。663314142×3=3×2（3×4）×0.25=3×（4×0.25）2×（3×4）=2×3+2×4第一组 新知探究探究1第二组观察下列各式，它们的积是正的还是负的？（2）[3×（-4）]×（-5）=3×[（-4)×(-5)]=，（1）5×（-6）=（-6）×5=，（3）5×[3+(-7)]=5×3+5×(-7)=。-30-306060-20-205×（-6）=（-6）×5[3×（-4）]×（-5）=3×[（-4)×(-5)]5×[3+(-7)]=5×3+5×(-7) 新知探究结论第一组式子中数的范围是，第二组式子中数的范围是，比较第一组和第二组的算式，可以发现。正数有理数各运算律在有理数内仍然适用 归纳总结两个数相乘，交换两个因数的位置，积相等。ab＝ba三个数相乘，先把前两个数相乘，或先把后两个数相乘，积相等。(ab)c＝a(bc)1.乘法交换律：2.乘法结合律：数的范围已扩充到有理数。注意：用字母表示乘数时，“×”号可以写成“·”或省略，如a×b可以写成a·b或ab。 归纳总结一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。3.乘法分配律：a(b＋c)ab＋ac＝根据乘法交换律和结合律可以推出：三个以上有理数相乘，可以任意交换因数的位置，也可先把其中的几个数相乘。根据分配律可以推出：一个数同几个数的和相乘，等于把这个数分别同这几个数相乘，再把积相加。a(b＋c＋d)＝ab＋ac＋ad 新知应用趁热打铁例1：计算：（－85）×（－25）×（－4）解：原式＝（－85）×［（－25）×（－4）］＝（－85）×100＝－8500解：原式=－8×(－0.125)×(－12)×(－)×(－0.1)=[－8×(－0.125)]×[(－12)×(－)]×(－0.1)=1×4×(－0.1)=－0.4变式计算：(－8)×(－12)×(－0.125)×(－)×(－0.1) 新知应用趁热打铁例2：用两种方法计算解法1：原式＝解法2：原式＝＝－1＝3＋2－6＝－1 新知应用观察思考计算：解法有错吗？错在哪里？？？？______解：原式＝＝－8－18＋4－15＝－41＋4＝－37－24×－24×＋24×－24× 新知应用观察思考正确解法：特别提醒：1.不要漏掉符号，2.不要漏乘。_______________________＝－8＋18－4＋15＝－12＋33＝21＝(－24)×＋(－24)×(－)＋(－24)×＋(－24)×(－) 梳理反思有理数的乘法运算律运算律内容字母表示乘法交换律两个数相乘，交换两个因数的位置，积不变。乘法结合律三个数相乘，先把前两个数相乘，或先把后两个数相乘，积不变。乘法分配律一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。a(b＋c)ab＋ac＝(ab)c＝a(bc)ab＝ba 课后练习计算：（1）(-7.5)×25××40；（2）(-13)×1.2+3×1.2. 谢谢