七年级下数学课件《幂的乘方》课件_冀教版 35页

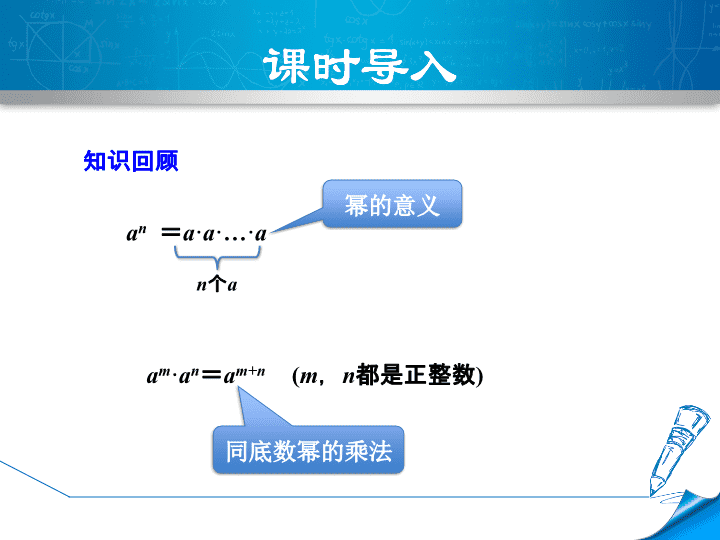
8.2 幂的乘方与积的乘方 第1课时 幂的乘方 第八章 整式的乘法 1 u幂的乘方法则 u幂的乘方法则的应用 2 逐点 导讲练 课堂 小结 作业 提升 an ＝a·a·…·a n个a 幂的意义 am·an＝am+n (m，n都是正整数) 同底数幂的乘法 知识回顾 练习 am·am=_________. a3·a3·a3=_________. 思考：怎样计算 (a4)3 (a3)5 1 幂的乘方法则 知1－导 1. 依据同底数幂乘法的性质，210×210×210=______. 根据乘方的意义， 210×210×210可以表示为______. 由此，能得到什么结论？ 2. (102)3表示3个102相乘，(102)3=10( ) (a3)4表示4个a3相乘，(a3)4 =a ( ) 3. 观察上面各式中幂指数之间的关系，猜想：若m，n 是正整数，则(am)n=______. 知1－导 事实上，根据乘方的意义及同底数幂乘法的性质， 对于正整数m，n，有 (am)n =am·am· … ·am =a m+m+ …+m = amn. n个am n个m (am)n = amn(m，n都是正整数). 幂的乘方，底数不变，指数相乘. 归 纳 （来自教材） 知1－导 知1－讲 (1)幂的乘方法则在推导过程中运用了乘方的意义和同 底数幂的乘法法则． (2)运用此法则时要明白，底数a可以是一个单项式， 也可以是一个多项式． (3)幂的乘方法则可以逆用，即amn＝(am)n＝(an)m. (4)幂的乘方与同底数幂的乘法都是底数不变，但容易 出现指数相乘与相加混淆的错误． 例1 把下列各式表示成幂的形式： (1) (103)4； (2) (c2)3； (3) (a4)m . 知1－讲 （来自教材） (⑴)(103)4 = 103×4 = 1012 ； (2) (c2)3 = c2×3 = c6 ； (3) (a4)m = a4×m = a4m. 解： 知1－讲 利用幂的乘方法则进行计算时，要紧扣法则的 要求，出现负号时特别要注意符号的确定和底数的 确定． 知1－练 （来自教材） 1 下列各式的计算是否正确？如果不正确.请改正过来. (1) (a2)3 =a5； (2) a2·a3 =a6 ； (3) a3 +a3 =a6； (4) (am)n＝(an)m(m，n都是正整数). (1)不正确，应为(a2)3＝a2×3＝a6. (2)不正确，应为a2·a3＝a2＋3＝a5. (3)不正确，应为a3＋a3＝2a3. (4)正确． 解： 计算： (1)(72)3； (2)(b4)3. 填空： (1)(33)3 =3( ) ； (2)(23)4 =2( ) ； (3)94 =3( ) ； (4)[(－3)3 ]5 =－3( ) . （来自教材） (1)(72)3＝72×3＝76. (2)(b4)3＝b4×3＝b12. 解： 2 知1－练 3 9 12 8 15 4 设m，n是正整数，计算： (1)(58)n； (2)(7m)5； (3)(98)n； (4)(2m)n. （来自教材） 知1－练 (1)(58)n＝58n ； (2)(7m)5＝75m ； (3)(98)n＝98n ； (4)(2m)n＝2mn. 解： 知1－练 【中考·安徽】计算(－a3)2的结果是(　　) A．a6 B．－a6 C．－a5 D．a5 【中考·宁波】下列计算正确的是(　　) A．a3＋a3＝a6 B．3a－a＝3 C．(a3)2＝a5 D．a·a2＝a3 5 A D6 知1－练 （来自教材） 【中考·岳阳】下列运算正确的是(　　) A．(x3)2＝x5 B．(－x)5＝－x5 C．x3·x2＝x6 D．3x2＋2x3＝5x5 下列运算正确的是(　　) A．4m－m＝3 B．m3·m4＝m7 C．(－m3)2＝m9 D．－(m＋2n)＝－m＋2n 7 B B8 例2 计算： (1) x·(x2)3； (2) a·a2·a3 －(a2)3. 知1－讲 (1) x·(x2)3 ＝ x·x2×3 ＝ x·x6 ＝x7. (2)a·a2·a3 －(a2)3 ＝ a6－ a6 ＝0. 解： （来自教材） 知1－讲 在幂的运算中，如果遇到混合运算，则应按有 理数的混合运算顺序进行运算；如果底数互为相反 数，就要把底数统一成相同的，然后再进行计算； 计算中不要将幂的乘方与同底数幂的乘法混淆． 知1－练 （来自教材） (1)(a3)2·a2＝a3×2·a2＝a6·a2＝a8. (2)(xm)4·x3＝x4m·x3＝x4m＋3. (3)(m2)n·mn＋1＝m2n·mn＋1＝m3n＋1. (4)xm·(x2m)3＝xm·x6m＝x7m. 解： 1 计算： (1)(a3)2·a2； (2)(xm)4·x3； (3)(m2)n·mn＋1； (4)xm·(x2m)3. 知1－练 设m，n是正整数，计算： (1)(m2)n·mn ； (2)(yn)2·(y3)m. 2 （来自教材） (1)(m2)n·mn＝m2n·mn＝m2n＋n＝m3n. (2)(yn)2·(y3)m＝y2n·y3m＝y2n＋3m. 解： 知1－练 （来自教材） (1)(a2)4·a2＋2(a3)2·(a2)2＝a8·a2＋2·a6·a4＝a10＋2a10 ＝3a10. (2)3(x2)2·x3－x·(x2)3＝3x4·x3－x·x6＝3x7－x7＝2x7. 解： 3 计算： (1)(a2)4·a2＋2(a3)2·(a2)2 ； (2)3(x2)2·x3－x·(x2)3. 知1－练 化简a4·a2＋(a3)2的结果是(　　) A．a8＋a6 B．a6＋a9 C．2a6 D．a12 【中考·孝感】下列运算正确的是(　　) A．a2＋a2＝a4 B．a5－a3＝a2 C．a2·a2＝2a2 D．(a5)2＝a10 4 C 5 D 计算： (1)[(z－y)2]3； (2)(ym)2·(－y3)； (3)(－x3)4·(－x4)3. 7 知1－练 (1)原式＝(z－y)2×3＝(z－y)6. (2)原式＝y2m·(－y3)＝－y2m＋3. (3)原式＝x12·(－x12)＝－x24. 解： 2知识点 幂的乘方法则的应用 知2－讲 amn=(am)n=(an)m（m、n均为正整数）. 即将幂指数的乘法运算转化为幂的乘方运算. 注意：逆用幂的乘方法则的方法是：幂的底数不变， 将幂的指数分解成两个因数的乘积，再转化成幂的 乘方的形式，如x8=(x4)2=(x2)4.至于选择哪一个变形 结果，要具体问题具体分析． 例3 若xm·x2m＝3，求x9m的值． 知2－讲 利用amn＝(am)n＝(an)m，可对式子进行灵活 变形，从而使问题得到解决． 导引： 因为xm·x2m＝3，所以x3m＝3， 因此x9m＝(x3m)3＝33＝27. 解： 本题运用整体思想将x3m看作一个整体，结合幂 的乘方法则的逆向运用使所求式子转化为这个整体 的幂.从而运用整体代入求出要求的值使问题获解. 知2－讲 （来自教材） (1)将[(a+b)2]4表示成以a+b为底的幂. (2)将[(2x+y)3]2表示成以2x+y为底的幂. 1 (1)已知(x2)m=x8，求m. (2)已知am=4，an=8，求 a2m+3n. 2 (1)[(a＋b)2]4＝(a＋b)2×4＝(a＋b)8. (2)[(2x＋y)3]2＝(2x＋y)3×2＝(2x＋y)6. 解： 知2－练 (1)(x2)m＝x2m＝x8，则2m＝8，m＝4. (2)a2m＋3n＝a2m·a3n＝(am)2·(an)3＝42×83＝16×512 ＝8 192. 解： 已知a＝－34，b＝(－3)4，c＝(23)4，d＝(22)6，则下 列a，b，c，d四者关系的判断，正确的是(　　) A．a＝b，c＝d B．a＝b，c≠d C．a≠b，c＝d D．a≠b，c≠d 3 知2－练 C 已知10x＝m，10y＝n，则102x＋3y等于(　　) A．2m＋3n B．m2＋n3 C．6mn D．m2n3 9m·27n可以写为(　　) A．9m＋3n　　 B．27m＋n C．32m＋3n　　 D．33m＋2n 4 5 D 知2－练 C 若3×9m×27m＝321，则m的值为(　　) A．3　　　　 B．4　　　　 C．5　　　　 D．6 若5x＝125y，3y＝9z，则x : y : z等于(　　) A．1 : 2 : 3 B．3 : 2 : 1 C．1 : 3 : 6 D．6 : 2 : 1 知2－练 6 B 7 D 若x，y均为正整数，且2x＋1·4y＝128，则x＋y的值 为(　　) A．3 B．5 C．4或5 D．3或4或5 已知x＋4y＝5，求4x×162y的值． 8 知2－练 C 因为x＋4y＝5，所以4x×162y＝4x×(42)2y＝ 4x×42×2y＝4x＋4y＝45＝1 024. 解： 9 已知275＝9×3x，求x的值． 知2－练 10 因为275＝9×3x， 所以(33)5＝32×3x. 所以315＝32＋x. 所以2＋x＝15. 所以x＝13. 解： 1 幂的乘方 幂的乘方，底数 不变，指数相乘 意义 正向应用： (am)n = amn(m， n都是正整数). 逆向应用： amn＝(am)n＝(an)m (m，n都是正整数). 解决实 际问题 2 易错小结 下列四个算式中正确的有(　　) ①(a4)4＝a4＋4＝a8；②[(b2)2]2＝b2×2×2＝b8； ③[(－x)3]2＝(－x)6＝x6；④(－y2)3＝y6. A．0个 B．1个 C．2个 D．3个 C 易错点：对幂的乘方运算法则理解不透导致出错 本题易错之处在于混淆幂的乘方与同底数幂的乘 法法则的运用．②③正确． 请完成《典中点》 Ⅱ 、 Ⅲ板块 对应习题！