- 101.55 KB
- 2021-10-25 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
《同步课时卷》北师大版七年级数学(下册)
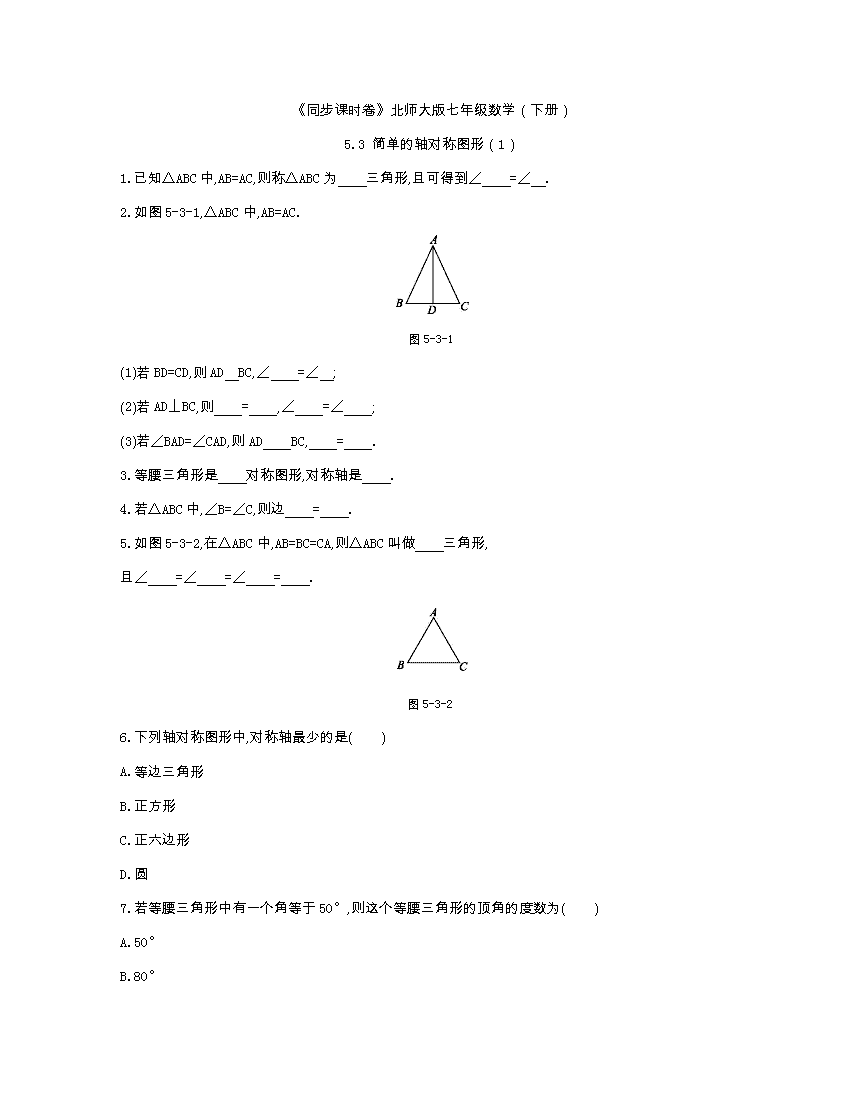
5.3 简单的轴对称图形(1)
1.已知△ABC中,AB=AC,则称△ABC为 三角形,且可得到∠ =∠ .
2.如图5-3-1,△ABC中,AB=AC.
图5-3-1
(1)若BD=CD,则AD BC,∠ =∠ ;
(2)若AD⊥BC,则 = ,∠ =∠ ;
(3)若∠BAD=∠CAD,则AD BC, = .
3.等腰三角形是 对称图形,对称轴是 .
4.若△ABC中,∠B=∠C,则边 = .
5.如图5-3-2,在△ABC中,AB=BC=CA,则△ABC叫做 三角形,
且∠ =∠ =∠ = .
图5-3-2
6.下列轴对称图形中,对称轴最少的是( )
A.等边三角形
B.正方形
C.正六边形
D.圆
7.若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
A.50°
B.80°
C.65°或50°
D.50°或80°
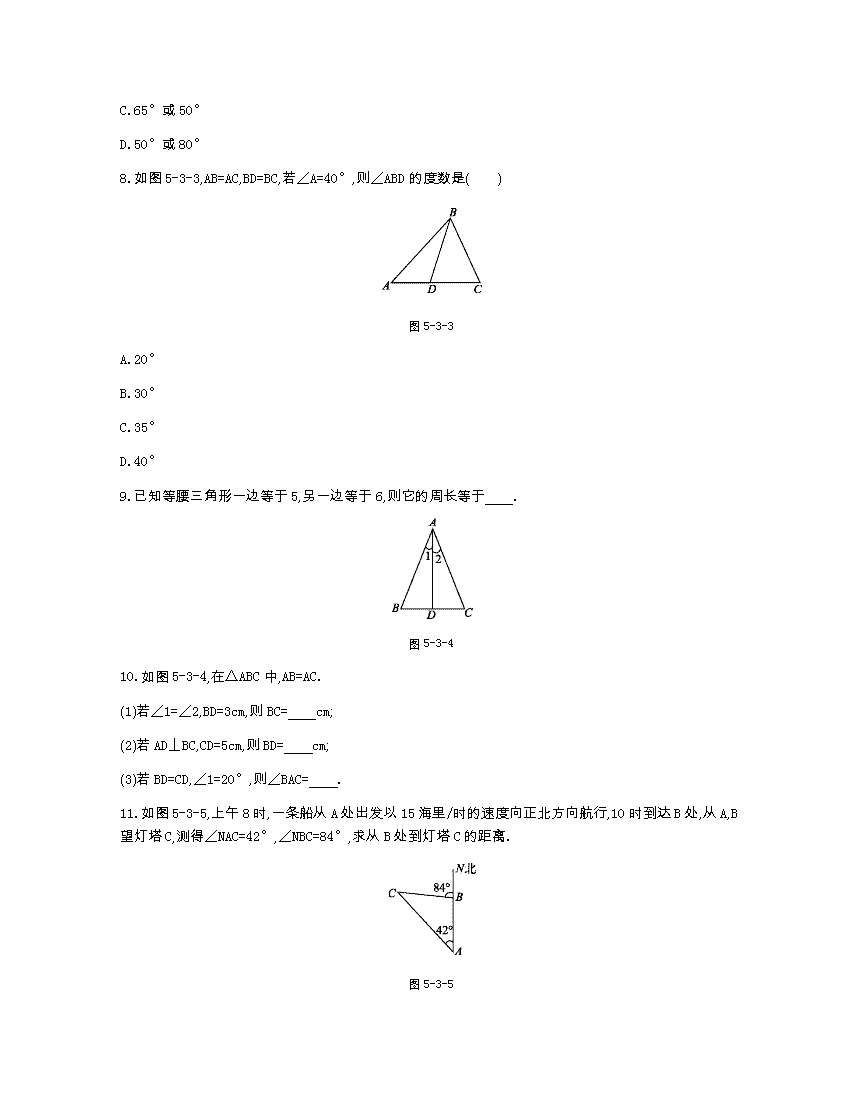
8.如图5-3-3,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是( )
图5-3-3
A.20°
B.30°
C.35°
D.40°
9.已知等腰三角形一边等于5,另一边等于6,则它的周长等于 .
图5-3-4
10.如图5-3-4,在△ABC中,AB=AC.
(1)若∠1=∠2,BD=3cm,则BC= cm;
(2)若AD⊥BC,CD=5cm,则BD= cm;
(3)若BD=CD,∠1=20°,则∠BAC= .
11.如图5-3-5,上午8时,一条船从A处出发以15海里/时的速度向正北方向航行,10时到达B处,从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°,求从B处到灯塔C的距离.
图5-3-5
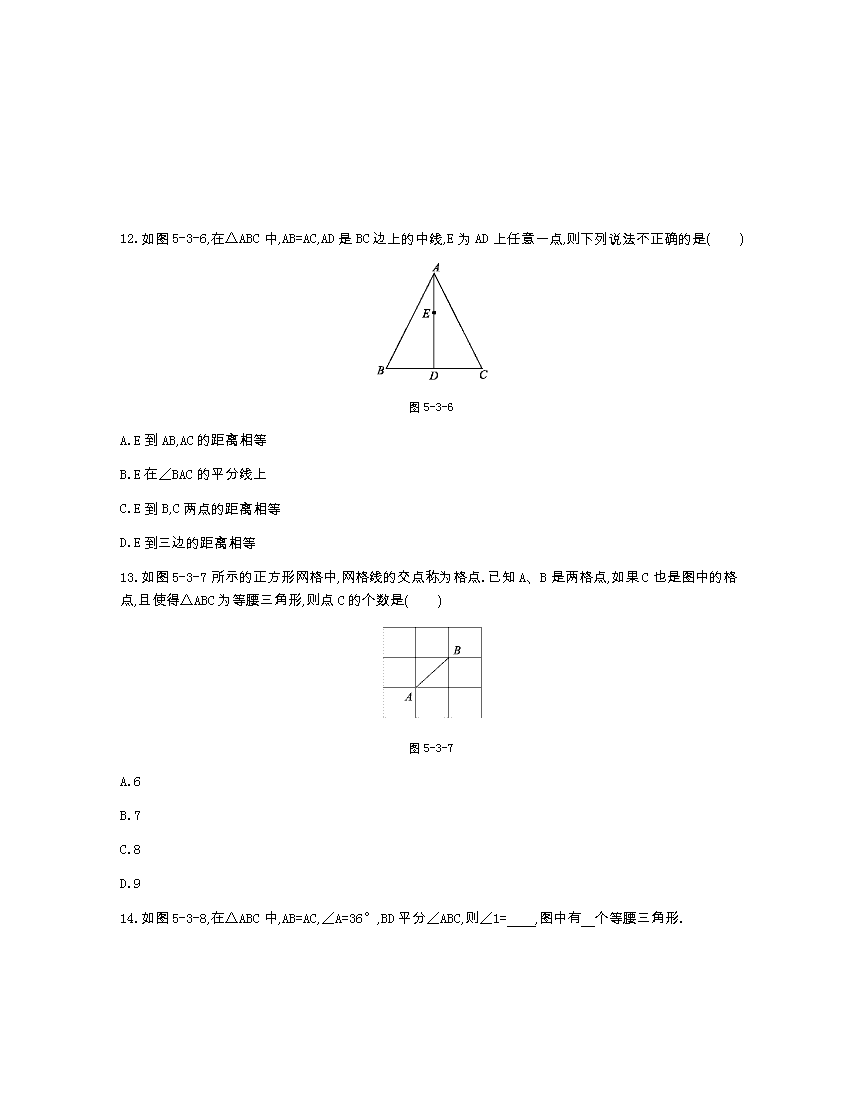
12.如图5-3-6,在△ABC中,AB=AC,AD是BC边上的中线,E为AD上任意一点,则下列说法不正确的是( )
图5-3-6
A.E到AB,AC的距离相等
B.E在∠BAC的平分线上
C.E到B,C两点的距离相等
D.E到三边的距离相等
13.如图5-3-7所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
图5-3-7
A.6
B.7
C.8
D.9
14.如图5-3-8,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,则∠1= ,图中有 个等腰三角形.
图5-3-8
15.如图5-3-9,已知△ABC是等边三角形,D,E,F分别在边BC,CA,AB上,且△DEF也是等边三角形,则图中除已知的边以外的相等的线段为 .
图5-3-9
16.如图5-3-10,在△ABC中,AD⊥BC于D.请你再添加一个条件,就可以确定△ABC是等腰三角形.你添加的条件是 .
图5-3-10
17.如图5-3-11,在河岸l的同侧有A,B两村,在河边修一水泵站P,使所用的水管最短,另修一码头Q,使Q到A,B两村的距离相等,试画出P,Q所在的位置.
图5-3-11
参考答案
1.等腰 B C
2.(1)⊥ BAD CAD
(2)BD CD BAD CAD
(3)⊥ BD CD
3.轴底边上的高(或顶角的平分线或底边上的中线)所在的直线
4.AB=AC
5.等边 A B C 60°
6.A
7.D
8.B
9.16或17
10.(1)6
(2)5
(3)40°
11.解:由题意知:
AB=2×15=30(海里).
因为∠CBN=84°,
所以∠CBA=96°.
所以∠C=180°-∠CBA-∠A=42°.
所以BC=AB=30(海里).
答:从B处到灯塔C的距离为30海里.
12.D
13.C
14.72° 3
15.AE=CD=BF,AF=CE=BD
16.BD=CD
17.解:如图所示:
作点A关于直线l的对称点A’,连接A’B,交直线l于点P,点P即可使所用的水管最短.根据线段垂直平分线的性质知,点Q应是线段AB的垂直平分线与直线l的交点.
相关文档
- 2020七年级数学上册 第三章实际问2021-10-255页
- 七年级下语文课件老王 (16)_鲁教版2021-10-2511页
- 人教版七年级上册语文导学案:从百草2021-10-257页
- 人教版七年级地理上册教案(62页)2021-10-2562页
- 七年级下语文课件记承天寺夜游 (162021-10-2523页
- 2020—2021学年七年级语文部编版下2021-10-2548页
- 七年级上数学课件《展开与折叠》 (2021-10-2524页
- 七年级上册语文课件《秋颂》 苏教2021-10-2510页
- 七年级道德与法治上册第一单元成长2021-10-254页
- 【名师打造】人教版七年级语文上册2021-10-253页