七年级下册数学课件《两条直线的位置关系 对顶角、余角和补角》 (7)_北师大版 35页

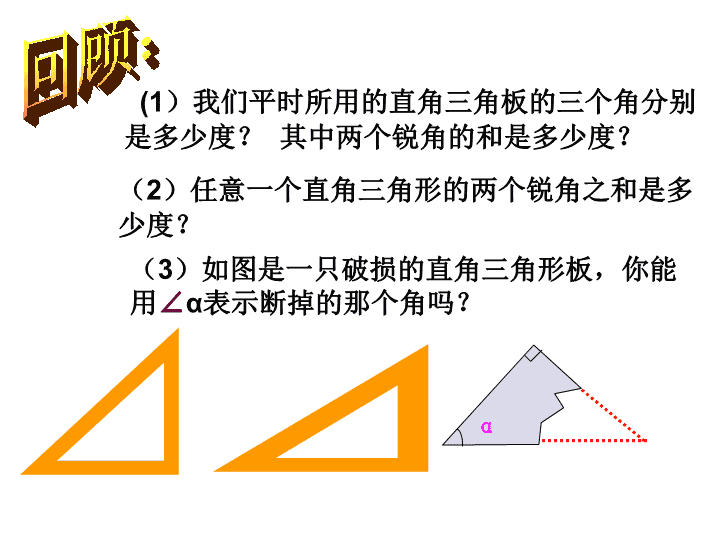
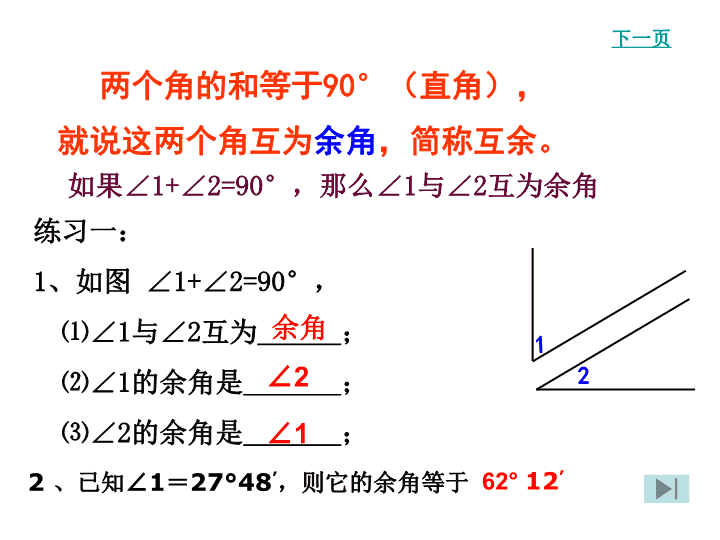
(1）我们平时所用的直角三角板的三个角分别 是多少度？ 其中两个锐角的和是多少度？ （2）任意一个直角三角形的两个锐角之和是 多少度？ （3）如图是一只破损的直角三角形板，你能 用∠α表示断掉的那个角吗？ α 两个角的和等于90°（直角）， 就说这两个角互为余角，简称互余。 练习一： 1、如图 ∠1+∠2=90°， ⑴∠1与∠2互为 ； ⑵∠1的余角是 ； ⑶∠2的余角是 ； 1 2 如果∠1+∠2=90°，那么∠1与∠2互为余角 2 、已知∠1＝27°48’，则它的余角等于 　 余角 ∠2 ∠1 62° 12’ 下一页 1 2 ∠1与∠2互余 ∟ 解：∵ ∠1与∠2互余 ∴ ∠1+∠2=900 或 ∠1=900－∠2 ∠2=900－∠1 画出∠COB的余角 C O B A D ⑵量一量: 用量角器量一下这两角的度数； 根据图形: ⑴猜一猜: ∠1 与∠2相等吗？ ∠1与∠COB互 余， ∠ 2与∠COB互 余 C O B A D (3)议一议：把结论归纳一下： (4)试一试：你还能用什么方法来说明这个结论？ 相等 同角的余角相等。 1 2 解： ∵ ∠1与∠COB互余， ∠ 2与∠COB互余 ∴ ∠1+ ∠BOC = 90 °，∠2+ ∠BOC = 90 ° ∴ ∠1= 90 °－ ∠BOC ∠2= 90 °－ ∠BOC ∴∠1 = ∠2 如图，∠1与∠COB互余， ∠ 2与∠COB互余 则∠1=∠2吗？ A O B D C 1 2 同角的 余角相等 如图∠AOB = 90 °， ∠COD = 90 ° 则∠1与∠2是什么关系？ 答： ∠1 = ∠2 解： ∵ ∠AOB = 90 °， ∠COD = 90 ° ∴∠1+ ∠BOD = 90 ° ∠2+ ∠BOD = 90 ° ∴∠1 = ∠2 A O B C D 1 2 如图，∠1与∠2互余，∠3与∠4互余， 如果∠1=∠3，那么∠2与∠4相等吗？为什么？ 1 2 34 解： ∠2与∠4相等 ∵ ∠1﹢∠2 = 90°， ∠3﹢∠4 = 90° ∴ ∠2 = 90°─∠1， ∠4 = 90°─∠3 ∵ ∠1 =∠3 ∴ ∠2 =∠4 等角的余角相等 A B C O 1 2 两个角的和等于180°（平角）， 就说这两个角互为补角，简称互补。 如果∠1+∠2=180°，那么∠1与∠2互为补角 12 思考：如何画一个已知∠BOC的补角？ B O C 如图，∠1是∠BOC 的补角， ∠2是∠BOC 的补角。 那么∠1与∠2相等吗? 解： ∠1与∠2相等。 ∵ ∠1+ ∠BOC = 180 ° ∠2+ ∠BOC = 180 ° ∴ ∠1=180 °－ ∠BOC ∠2= 180 ° －∠BOC ∴ ∠1 = ∠2 A O B D C 1 2 同角的 补角相等 如图，∠1与∠2互补，∠3与∠4互补， 如果∠1=∠3，那么∠2与∠4相等吗？为什么？ 解： ∠2与∠4相等 ∵ ∠1﹢∠2 = 180°， ∠3﹢∠4 = 180° ∴ ∠2 = 180°─∠1， ∠4 = 180°─∠3 ∵ ∠1 =∠3 ∴ ∠2 =∠4 等角的补角相等 1 2 4 3 判断：（正确的打“√”，错误的打“╳”。） ①一个角的余角一定是锐角（ ） ②一个角的补角一定是钝角（ ） ③若∠1+∠2+∠3=90°，那么∠1、∠2、∠3 互为余角（ ） √ ╳ ╳ 例1.填表 一个角 的度数 40º 60º12’24” xº(x<90º) 这个角 的余角 60º 这个角 的补角 45º 120º 50º 140º 135º 30º 150º 30º 60º 29º47’36” 150º12’24” 90º ─ xº 180º ─ xº 收获: ①求∠α 的余角的计算方法为 90º ─ ∠α (∠α <90º ) ②求∠α 的补角的计算方法为180º ─ ∠α (∠α <180º ) ③同一个角的余角与补角的关系是: ∠α 的余角+ 90º= ∠α 的补角(∠α <90º ) 若∠1 + ∠2 =180 °, 则 .( ) 若∠1和∠2互补, 则 .( ) 若∠3 + ∠4 =90 °, 则 .( ) 若∠3和∠4互余, 则 .( ) 3 4 1 2 ∠1和∠2互补 互补定义 ∠1 + ∠2 =180 °互补定义 ∠3和∠4互余 互余定义 ∠3 + ∠4 =90 °互余定义 109 °21 ′19 °21 ′ （90-x） ° （180-x） ° 60 ° 两直线相交形成了∠1、∠2、∠3和∠4 , 其中的∠1和∠3叫做对顶角，∠2和∠4也是 对顶角. 1 2 1、有公共的顶点； 对顶角应具备的条件： 2、一个角的两边是另一角两边的反向延长线； （也就是说，一定要是两条直线相交形成的） 下列各图中，∠1与∠2是对顶角的是（ ） 1 2 A 1 2 B 1 2 C 1 2 D D 练一练 1 2 3 4 对顶角的特征: 1. 有共同的顶点 2. 其中一个角的两边在另一个角两 边的延长线上 A 1 2 B 1 2 C 1 2 D 1 2 如果两个角是对顶角，那 么这两个角相等吗? 对顶角相等 考考你：相等的两个角是对顶角吗？ 例2 如图，两直线相交 形成的四个角中, ∠1=30°，那么 ∠2、∠3和∠4 各等于多少度? 例3 如图O是直线AB上一点,OE平分∠AOC,OD平分∠BOC 那么图中共有: (⑴)几对相等的角 (2) 几对互余的角 (3)几对互补的角 解: 相等的角: ∠1 = ∠2 , ∠3= ∠4 互余的角: ∠2与∠3, ∠1与 ∠4 ,∠1与 ∠3, ∠2 与∠4 互补的角: ∠1与∠BOE, ∠4与∠AOD, ∠AOC与∠BOC, ∠2 与BOE, ∠3与∠AOD A B E C D 1 2 3 4 O A O B E D C 1. ∠1=120 °, ∠1与∠2互补, ∠3与∠2互余,则 ∠3= . 2.O为直线AB上的一点，OD 平分∠AOB， ∠COE = 90 ° 则∠BOC = 　 　， ∠COD = 　 　。 检测 ∠DOE ∠AOE 30 ° A B C D E F G ∠AOB内部画99条射线，问图中 一共有多少个角？ 从特殊性想起： 角内没画射线——1个角 角内画1条射线——(1+2)个角 角内画2条射线——(1+2+3)个角 …… 角内画99条射线—— 1+2+3+4+…+100=5050个角 （3）要测量两堵墙所成的角的度数， 但人不能进入围墙，如何测量 ？ A B O C D 猜谜语： （打一数学概念） 谜底：对顶角 互为余角 互为补角 对顶角 对应图形 数量关系 性 质 1 2 ∠1+ ∠2 = 90° 同角（或等角） 的余角相等。 12 ∠1+ ∠2 = 180° 同角（或等角） 的补角相等。 21 3 4 对顶角相等 ∠1= ∠3 ∠2= ∠4 作业 （A）课本P158练习第2题； P159习题第3、7题 （B） P159习题第3、7、8题 解：∵ ∠1+∠2=90° ∴∠1与∠2互余 “互为余角的定义”用数学语言表示 如下： （互余定义） （已知） 解：∵ ∠1+∠2=180° ∴∠1与∠2互补 “互为补角的定义”用数学语言表示 如下： （互余定义） （已知）