七年级下册数学课件《立方根》 人教新课标 (9) 22页

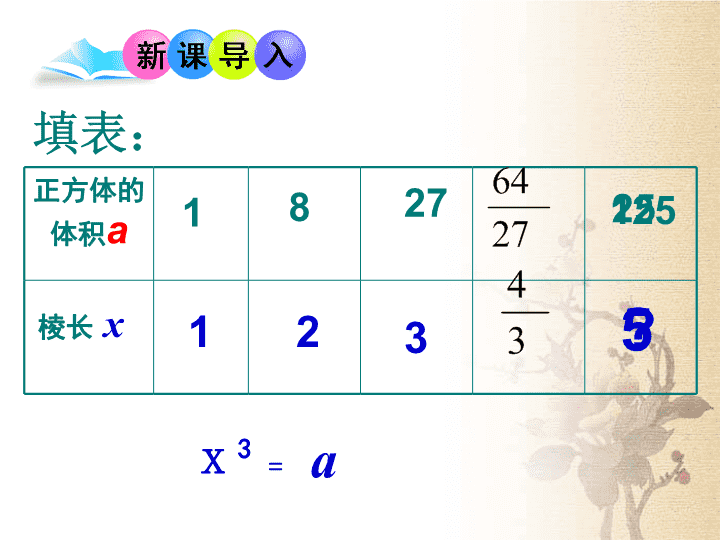
立 方 根 6.2 立方根 七年级数学课件 要做一个体积为27cm3的正方体模型（如图）， 它的棱长要取多少？你是怎么知道的？ 思考：(1)什么数的立方等于-8？ (2)如果问题中正方体的体积为5cm3，正方 体的棱长又该是多少？ 设正方体的棱长为X㎝,则 3 27x  这就是要求一个数,使它的立方等于27. 因为 33 27 所以 X=3. 正方体的棱长为3㎝ -2 正方体的 体积a 1 2 3 1 27 棱长 x 3x = a 8 2527 64 3 4 填表： ?5 125 立方根的概念. 　　一般地，如果一个数的立方等于a，这个 数就叫做a的立方根(也叫做三次方根).用式子表示，如果X3 =a，那么X叫做a的立方根. 2 a 或 a 表示的立方根用数 3 aa 1.立方根的概念. 　　一般地，如果一个数的立方等于a，这个数就叫 做a的立方根(也叫做三次方根). 　用式子表示，如果X3 =a，那么X叫做a的立方根. 3 a数a的立方根用符号“ ”表示,读作“三次根号a”， 其中a是被开方数,3是根指数(注意:根指数3不能省略). 3273  a3 被开方数 根指数 ∵( )3=-8，∴ 是-8的立方根 ∵( )3=1，∴ 是1的立方根 ∵( )3=0，∴ 0的立方根是 ∵( )3=-64，∴ -64的立方根是 -2 -2 1 1 0 0 -4 -4 立方根的表示方法. 3 a根指数 根号 被开方数 283 即 283 即 a a 3 a， ， ， a a 3 a 4 a 4 a 思考： 如果正方体的体积为5cm3，正方体的棱 长又该是多少？ 设正方体的棱长为X,则 3 5x  所以正方体的棱长是 3 5 ㎝. 2.开立方. 　　求一个数的立方根的运算，叫做开立方. 开立方与立方也是互为逆运算，因此求一个数 的立方根可以通过立方运算来求. （１） 因为2 =8，所以8的立方根是（　）； （２） 因为( ) =0.125,所以0.125的立方根是（　）； （３）因为( ) ＝０，所以０的立方根是（　）； （４）因为 ( ) ＝－8，所以－8的立方根是（ ）； （５）因为( ) ＝－ －，所以－－ 的立方根（ ） 3 3 3 3 27 27 88 活动二 启发诱导,探索新知 2 0.5 0.5 0 0 2 2 3 2 3 2 探究题中正数、0和负数的立方根各有 什么特点? 1. 探究 3 3 正数有立方根吗？如果有，有 几个? 负数呢？零呢？ 一个正数有一个正的立方根； 一个负数有一个负的立方根， 零的立方根是零。 立方根的特征 讨论:你能归纳出平方根和立方根的异同点 吗? 被开方数 平方根 立方根 有两个互为相反数 有一个,是正数 无平方根 零 有一个,是负数 零 正数 负数 零 归 纳 总 结 练习:1、下列说法是否正确,并说明理由 (1) 的立方根是 ( ) (2) 负数不能开立方 ( ) (3) 4的平方根是2 ( ) (4)立方根是它本身的数只有零( ) (5)平方根是它本身的数只有零( ) (6) 的立方根是4 ( ) 64 27 4 3 64 √ × × × × × 3.求下列各数的立方根： （1）1，（2）-1 ，（3） -0.000008 （4）343 _____125 ,125(_____) (1) 33  _____125 64 ,125 64(_____) (2) 33  练习2.填空： -5-5 5 4 5 4 练一练 1.判断下列说法是否正确,并说明理由 x (2) 25的平方根是5 x (3) -64没有立方根 x (4) -4的平方根是 2 x (5) 0的平方根和立方根都是0 √ (1) 8 27 的立方根是 2 3  立方根是它本身的数有那些? 有1, -1, 0 平方根是它本身的数呢? 只有0 想一想 算术平方根是它本身的数呢? 有1, 0 引伸探究2 因为 = 3 8 , 3 8 = 3 8 3 8所以 3 273 27因为 = , = 3 27 3 27所以 猜一猜: 你能从上述问题中总结出互为相反数的两个数a与 -a的立方根的关系吗? a3-a3 = -2 -2 = -3-3 互为相反数的数的 立方根也互为相反 数 例:求下列各式的值 3 64 273 64(1) (2) (3)3 125 解: 3 64(1) =4 3 125(2) = 3 125 =-5 273 64(3) 273 64= = 3 4- 归纳: 求一个负数的立方根,可以先求出这个负数绝 对值的立方根,然后再取它的相反数. 下列式子表示什么意义？ 你能求出它们的值吗？ ;64)1( 3 ;125)2( 3  ;64 27)3( 3  ;)3()4( 3 3 ;64 32)5( 3  1.分别求下列各式的值： 3 1000 (1) 3 001.0 (2)  3 125 64 - (4)3 1)3(  3 216)5(  3 27 174)6(  101000 (1) 3  1.0001.0 (2) 3  11)3( 3  5 4 125 64)4( 3  6216)5( 3  3 5 27 125 27 274)6( 33   33 9)7(   99)7( 33  3 343)1( x 3 1251)2( x 23 x 423 x (2) 已知 一个立方体的体积为7cm3, 则它的表面积为多少? (1) x3= -0.008 ,则x的值为多少？ 思考: 相同点: ①0的平方根、立方根都有一个是0 ②平方根、立方根都是开方的结果。 不同点：①定义不同 ②个数不同 ③表示方法不同 ④被开方数的取值范围不同 1.立方根的定义,性质,计算. 2.立方根与平方根的异同 表示a 即 24  3 a 即 283  3.如果3x+16的立方根是4，求 2x+4的算术平方根. 3 34. 5 6 0, .x y x y    若 求 的值 .的值互为相反数，求34与42若.5 33 y xxy 