七年级下册数学课件《两条直线的位置关系 对顶角、余角和补角》 (5)_北师大版 17页

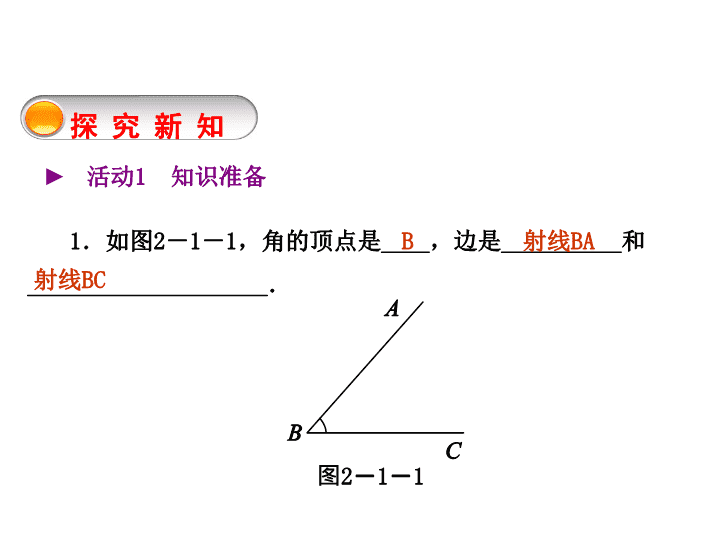
探究新知 探究新知 重难互动探究 重难互动探究 新知梳理 新知梳理 探 究 新 知 第1课时　对顶角、余角和补角 ► 活动1　知识准备 1．如图2－1－1，角的顶点是____，边是__________和 ____________________． 图2－1－1 B 射线BA 射线BC 第1课时　对顶角、余角和补角 2．如图2－1－2所示，从O点出发有OA，OB，OC，OD四条射 线，则图中有____个角． 图2－1－2 6 第1课时　对顶角、余角和补角 ► 活动2　教材导学 用量角器量出图中∠1，∠2，∠3，∠4的度数，这些角度 之间有什么关系？ [答案] 度数略 相等：∠1＝∠3，∠2＝∠4. 互补：∠1与∠2，∠3与∠4，∠1与∠4，∠2与∠3. 第1课时　对顶角、余角和补角 图2－1－3 第1课时　对顶角、余角和补角 2．探究余角及其性质 (1)在三角尺中，有一个角是90°，那么其余两个角的和是 ____________． (2)如图2－1－4所示，两块三角尺进行如下操作后，∠1＋ ∠2＝___________． 图2－1－4 90° 90° ◆ 知识链接——[新知梳理]知识点二、三 新 知 梳 理 第1课时　对顶角、余角和补角 ► 　知识点一　相交线与平行线 若两条直线只有一个公共点，我们称这两条直线为相交线． 在同一平面内，不相交的两条直线叫做平行线． [注意] “在同一平面内”这个前提条件不可缺少，因为在 空间里存在既不相交也不平行的两条直线．因此，初中阶段研 究的平行关系是指在同一平面内． 第1课时　对顶角、余角和补角 ► 　知识点二　对顶角 如果两个角有____________，且它们的两边互为 ____________，那么具有这种位置关系的两个角叫做对顶角． 对顶角________． 公共顶点 反向延长线 相等 第1课时　对顶角、余角和补角 ► 　知识点三　互为余角、互为补角的概念 如果两个角的和是90°，那么称这两个角互为________．如 果两个角的和是180°，那么称这两个角互为________． 余角 补角 第1课时　对顶角、余角和补角 ► 　知识点四　互为余角、互为补角的性质 同角(或等角)的余角_______，同角(或等角)的补角____． 解读：同角的余角相等指的是两个角是同一个角的余角，那 么这两个角相等；而等角的余角相等指的是两个角分别是两个 相等角的余角，那么这两个角相等． 相等 相等 第1课时　对顶角、余角和补角 注意：(1)互余关系与互补关系是指两个角之间的关系，如 ∠α＋∠β＋∠γ＝90°，则∠α，∠β，∠γ不可以说是互 余关系，同样∠1＋∠2＋∠3＝180°，也不可以说∠1，∠2， ∠3是互补关系； (2)互余(互补)关系只是一种数量关系，只要两个角的和为 90°(180°)，则两角就是互余(互补)关系，与两角的位置无关 . 重难互动探究 第1课时　对顶角、余角和补角 探究问题一　对顶角性质的运用 例1 如图2－1－5所示，直线AB，CD，EF相交于点O，且 ∠AOC＝80°，∠1＝50°，求∠2的度数． 图2－1－5 [解析] 先求∠COE的度数，再利用对顶角的性质解答． 第1课时　对顶角、余角和补角 解：因为∠AOC＝80°，∠1＝50°， 所以∠COE＝∠AOC－∠1＝80°－50°＝30°， 所以∠2＝∠COE＝30°. [归纳总结] 对顶角的特征： (1)是两个角；(2)有一个公共点； (3)角的两边互为反向延长线，所以两条直线相交，就构成 了两对对顶角； (4)对顶，说明了两个角的位置关系． 第1课时　对顶角、余角和补角 探究问题二　互为余角和互为补角的性质的运用 第1课时　对顶角、余角和补角 第1课时　对顶角、余角和补角 第1课时　对顶角、余角和补角 [归纳总结] 涉及几何中角的大小的计算时，利用方程知识 求解是最常用的方法，这会使计算过程简洁明了．