数学冀教版七年级上册教案1-10有理数的乘方 3页

- 1 - 1.10 有理数的乘方 教学目标 【知识与能力】 1．会进行有理数的乘方运算； 2．知道一个正数的任何次幂都是正数，一个负数的奇次幂是负数，一个负数的偶次幂是正 数． 【过程与方法】 通过实际背景感受乘方的意义，探索乘方运算的方法，发展观察、分析、比较、归纳、概括 的能力。 【情感态度价值观】 提高动手动脑的水平，体会数学与现实生活的联系。 教学重难点 【教学重点】 有理数的乘方运算。 【教学难点】 有理数乘方运算的符号法则。 课前准备 无 教学过程 一、引入课题： 师：有些时候，我们会遇到几个相同因数相乘的式子，比如五个 4 相乘，我们要写很长，这 样的式子有更简单的表示方式吗？（板书课题：有理数的乘方） 小学时我们学过正方形的面积公式和体积公式，谁还记得是什么？ 生：边长为 a 的正方形面积公式是 a2，边长为 a 的正方形体积公式 a3。 师：我们再来一起回忆一下：1 米=？分米，1 分米=？厘米，1 厘米=？毫米 生：1 米=10 分米，1 分米=10 厘米，1 厘米=10 毫米。 师：这样就有 1 米＝10 分米 ＝1010 厘米 ＝101010 毫米 在这里，10×10，10×10×10 都是相同因数相乘，为方便起见，我们把 10×10 记作 210 ， 读作 10 的二次方（或 10 的平方）；10×10×10 记作 310 ，读作 10 的三次方（或者 10 的立 方）。 二、一起探究： 师：同学们猜想一下，10×10×10×10 怎么表示，十个 10 相乘可以怎么表示？ 生：思考，回答 下面仿照上面的记数方法表示一列各式： （1） 5 5 5  可记作 ，3 3 3 3   可记作 ． （2）( 4) ( 4) ( 4) ( 4)       可记作 ， 1 1 1( ) ( ) ( )2 2 2      可记作 。 - 2 - 以上我们用更简便的方法将几个相同因数的积表示了出来，一般来说，ｎ个相同的因数 a 相乘， 10 a a a a a    个 记作 na ，即 10 a na a a a a    个 。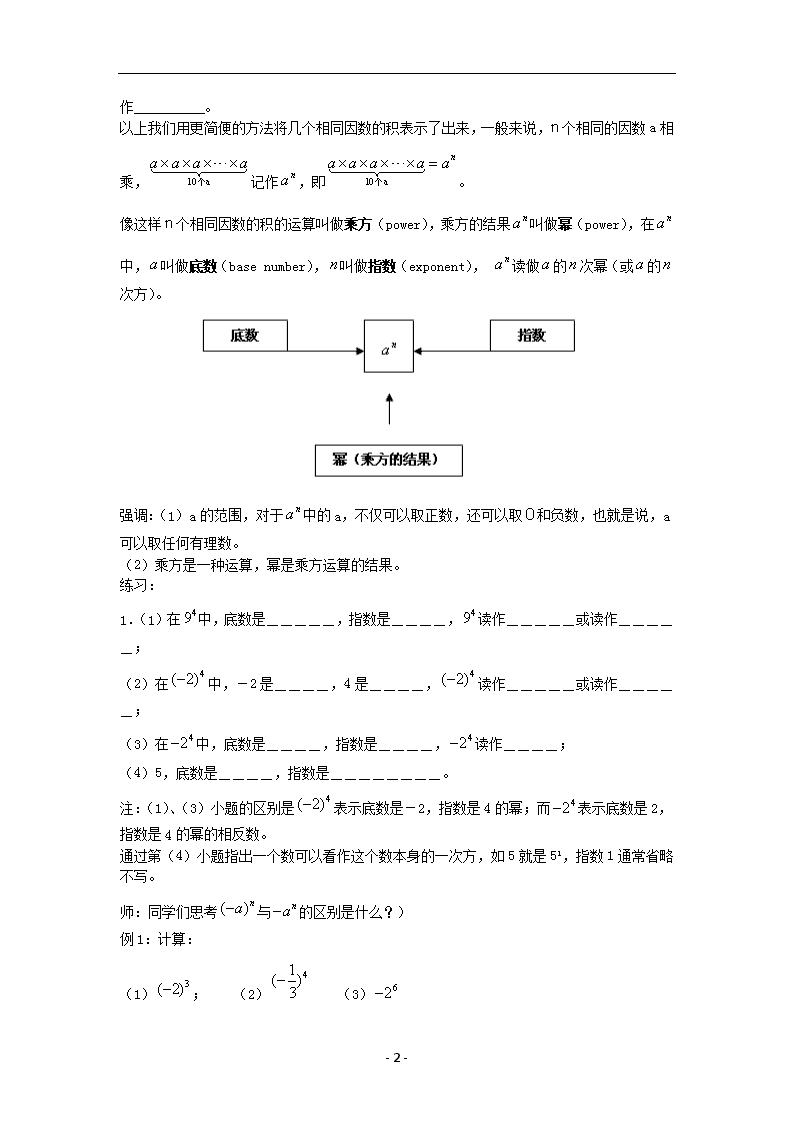 像这样ｎ个相同因数的积的运算叫做乘方（power），乘方的结果 na 叫做幂（power），在 na 中， a 叫做底数（base number），n 叫做指数（exponent）， na 读做 a 的 n 次幂（或 a 的 n 次方）。 强调：（1）a 的范围，对于 na 中的 a，不仅可以取正数，还可以取０和负数，也就是说，a 可以取任何有理数。 （2）乘方是一种运算，幂是乘方运算的结果。 练习： 1．（1）在 49 中，底数是＿＿＿＿＿，指数是＿＿＿＿， 49 读作＿＿＿＿＿或读作＿＿＿＿ ＿； （2）在 4( 2) 中，－2 是＿＿＿＿，4 是＿＿＿＿， 4( 2) 读作＿＿＿＿＿或读作＿＿＿＿ ＿； （3）在 42 中，底数是＿＿＿＿，指数是＿＿＿＿， 42 读作＿＿＿＿； （4）5，底数是＿＿＿＿，指数是＿＿＿＿＿＿＿＿。 注：（1）、（3）小题的区别是 4( 2) 表示底数是－2，指数是 4 的幂；而 42 表示底数是 2， 指数是 4 的幂的相反数。 通过第（4）小题指出一个数可以看作这个数本身的一次方，如 5 就是 51，指数 1 通常省略 不写。 师：同学们思考 ( )na 与 na 的区别是什么？） 例 1：计算： （1） 3( 2) ； （2） 41( )3  （3） 62 解：（1） 3( 2) ＝ ( 2)( 2)( 2) 8     ； - 3 - ( 2) ( 2)   可简记为 ( 2)( 2)  或 ( 2) ( 2)  （2） 41( )3  ＝ 1 1 1 1 1( )( )( )( )3 3 3 3 81      （3） 62 ＝ 2 2 2 2 2 2 64        三、做一做 1．在一表的空格处填写运算结果： 1( 2) 2( 2) 3( 2) 4( 2) 5( 2) 6( 2) …… …… 2．上表计算结果的符号有什么规律？ 提示：符号和指数有什么关系？ 师：负数的奇数次幂是负数，负数的偶次幂是正数。 思考：正数有这样的情况么？正数的奇数次幂是负数，负数的偶次幂是正数么？ 都是正数。所以，正数的任何次幂都是正数。那么 0 呢？ 总结：正数的任何次幂都是正数；负数的奇次幂是负数，负数的偶次幂是正数；0 的任何次 幂都是 0。 练习：P47 1，2 四、小结 今天我们学习了有理数的乘方，同学们有什么收获？