七年级下册数学课件《平面直角坐标系》 人教新课标 (9) 32页

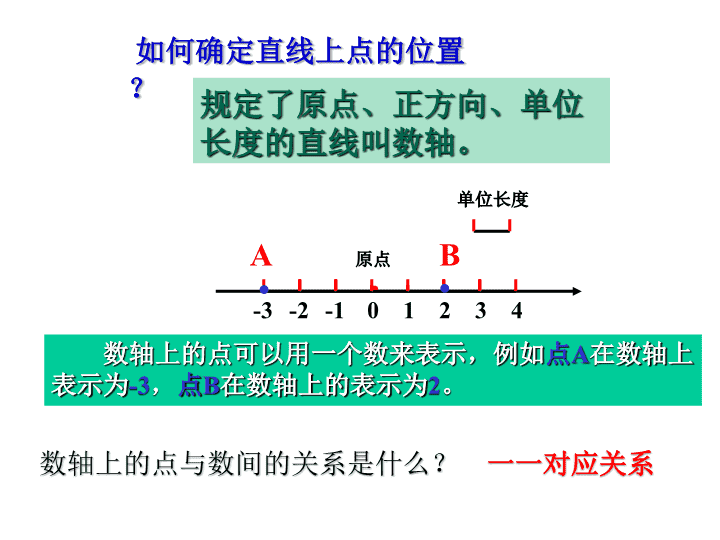
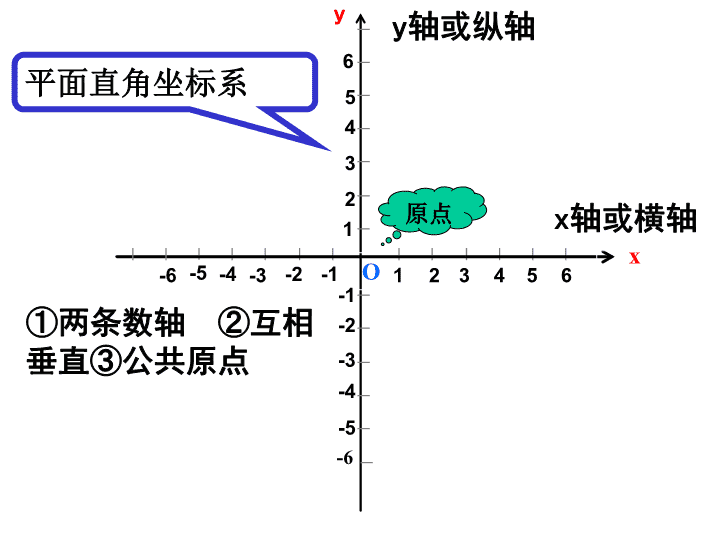
· 单位长度 0 1 2 3 4-3 -2 -1 原点 • • A B 3 1 4 2 5 -2 -4 -1 -3 0 1 2 3 4 5-4 -3 -2 -1 3 1 4 2 5 -2 -4 -1 -3 3 1 4 2 5 -2 -4 -1 -3 3 1 4 2 5 -2 -4 -1 -3 平面直角坐标系 如何在平面内确 定点的位置？ 5 -5 -2 -3 -4 -1 3 2 4 1 -6 6 O-5 5-3-4 4-2 3-1 21-6 6 x轴或横轴 y轴或纵轴 原点 ①两条数轴　②互相 垂直③公共原点 平面直角坐标系 x y X -3 -2 -1 1 2 3 3 2 1 - -2 -3 Y O 下面四个图形中，是平面直角坐标系的是（ ） X X Y （A） 3 2 1 -1 -2 -3 X Y （B） 2 1 -2 O -3 -2 -1 1 2 3 3 2 1 - -2 -3（C） O -3 -2 -1 1 2 3 3 2 1 -2 -3 Y （D） O D自学检测： ·Pb 0 a x 横轴 y纵轴 a叫做P的横坐标，b叫做P的纵坐标 有序数对(a, b)就叫做P的坐标 横坐轴 写在前面 记作：（a,b） 对于平面内任意一点Ｐ，过点Ｐ分 别向Ｘ轴、y轴作垂线，垂足在Ｘ轴、 y轴上对应的数分别是a,b x1 2 3 4 1 0 4 3 2 –2 –1 –1 –2 –3 –4 –3–4 Y A B C D EF 例1、写出图 中的多边形的 各个顶点坐标 A（-2，0） B（0，-3） C（3，-3） D（4，0） E（3，3） F（0，3） 解决问题： 如图，以中心广场为 坐标原点，取正东方 向为x轴的正方向， 取正北方向为y轴的 正方向，一个方格的 边长作为一个单位长 度，建立直角坐标系， 分别写出图中各个景 点的坐标。 各个景点的坐标是： 碑林（３，１） 雁塔（０，３） 钟楼（－２，１） 大成殿（－２，－２） 科技大学（－５，－７） 影月湖（０，－５） 中心广场（０，０） (3,0) （0，5） 例1：请你说出点A、B、C、D、E 、F在直角坐标系中的位置。 （4，3）（-2，3） （-4，-1） （2，-2） 0 1 2 3 4 5-4 -3 -2 -1 3 1 4 2 5 -2 -4 -1 -3 x横轴 y纵轴 ·C ·A ·B D· E• •F ·B 3 1 4 2 5 -2 -4 -1 -3 0 1 2 3 4 5-4 -3 -2 -1 x 横轴 y纵轴 ·C ·A ·E·D ( 2，3 ) ( 3，2 )( -2，1 ) ( -4，- 3 ) ( 1，- 2 ) 练习１、写出图中A、B、C、D、E各点的坐标。 1．平面直角坐标系中，点A(3,2)与B(2,3)是 同一个点吗?点C(-2,1)与E(1,-2)是同一个点 吗? 2.在平面直角坐标系下，点与实数对之间有何 关系？ 思考 对比 坐标平面上的点P与有序实 数对（a,b）一一对应。 3 1 4 2 5 -2 -4 -1 -3 0 1 2 3 4 5-4 -3 -2 -1 x 横轴 y纵轴 原点 第一象限 第四象限第三象限 第二象限 注 意:坐标轴上的点不属于任何象限。 例1、写出如图所示 的六边形ABCDEF 各个顶点的坐标 解： A（-2，0） B（0，-3） C（3，-3） D（4，0） E（3，3） F（0，3） 坐标轴上的点的坐标至少有一个为０， x轴上的点的纵 坐标都为0， y轴上的点的横坐标都为0 坐标轴上的点的坐标有什 么特点？ .任何一个在x轴上的点的纵坐标都为0。记作P(a , 0) .任何一个在y轴上的点 的横坐标为0。记作P(0 , b) 什么叫做点到直线的距离? 点到直线的垂线段的长度 例1、写出如图所示 的六边形ABCDEF 各个顶点的坐标 解： A（-2，0） B（0，-3） C（3，-3） D（4，0） E（3，3） F（0，3） 线段BC的位置有什么特点, B 与C的坐标之间有什么关系 ？ 线段BC平行于Ｘ轴，Ｂ、Ｃ两点的纵坐标相同。 纵坐标相同的点在平行于x轴的同一直线上 例1、写出如图所示 的六边形ABCDEF 各个顶点的坐标 解： A（-2，0） B（0，-3） C（3，-3） D（4，0） E（3，3） F（0，3） 线段CE的位置有什么特点， Ｃ与Ｅ的坐标之间有什么关系 ？ 线段CE平行于y轴，Ｃ、Ｅ两点的横坐标相同 横坐标相同的点在平行于y轴的同一直线上 3 1 4 2 5 -2 -4 -1 -3 0 1 2 3 4 5-4 -3 -2 -1 x 横轴 y纵轴 ·B ·A ·D ·C E 3 2 4 3 什么叫做点到直线的距离? 点到直线的垂线段的长度 ··· · · ·· · ·· · 想一想 在平面直角坐标系中分别描出下列点的坐标 A(3,2) B(3,-2) C(-3,2) D(-3,-2) E(4,2) A(3,2) B(3,-2) -2 -1 4321 x-3-4 -4 y 1 2 3 -3 -1 -2 C(-3,2) D(-3,-2) 0 点A与点B的坐标有什么关系? 点A与点B的位置有什么特点? 点A与点C的坐标有什么关系? 点A与点C的位置有什么特点? 点B与点C的坐标有什么关系? 点B与点C的位置有什么特点? 关于x轴对称的点的横坐标相同,纵坐标相反 关于y轴对称的点的纵坐标相同,横坐标相反 关于原点对称的点的横坐标、纵坐标都相反 练习 填空： (1)已知点P(3,1),则它关于x轴的对称点坐标 . (2)已知点P(3,1),则它关于y轴的对称点坐标 . (3)已知点P(3,1),则它关于原点的对称点坐标 . (4)已知点P(x，6)与Q(2，Y)关于原点对称，则 x= ，y= . （5）如果点 在第一象限，那么点 在（　　）. ( , )E a a  2( , 2 )a a  A、第四象限　　　　B、第三象限　　　　 C、第二象限　　　D、第一象限 (-3,1) (3,-1) (-3,-1) -2 ＿6 C A(3,3) -2 -1 4321-3-4 -4 1 2 3 -3 -1 -2 0 x y想一想 如图,点A在x轴正半轴与y轴正半轴 构成的角平分线上吗? 一.三象限角平分线上的点的 坐标有什么特点? B(-4,-4) 点B呢? 一.三象限角平分线上的点的横坐标与纵坐标相同; C(-2,2) 点C呢? 二.四象限角平分线上的点的 坐标有什么特点? 二.四象限角平分线上的点的横坐标与纵坐标相反; D(3,-3) 1.在 y轴上的点的横坐标是（ ）， 在 x轴上的点的纵坐标是（ ）. 2.点 A（2，- 3）关 于 x 轴 对 称 的 点 的 坐 标 是（ ）. 3.点 B（ - 2，1）关 于 y 轴 对 称 的 点 的 坐 标 是（ ）. 4.点 关于 轴的对称点的坐标是（　　）. ( , )a b y D A(a,b) B(a,-b) C(a,b) D(-a,b) 0 0 2,3 2,1 5.点 M（- 8，12）到 x轴的距离是 （ ），到 y轴的距离是（ ） 6.点（4，3）与点（4，- 3）的关系 是【 】. （A）关于原点对称 （B）关于 x轴对称 （C）关于 y轴对称 （D）不能构成对称关系 12 8 B 1.点 位于 轴左方，距 轴3个单位长，则点 的坐标 可能是（　　　）. P yy P A、（3，－４） B、（－３，４） C、（４，－３） D、（－４，３） 2.直角坐标系中，点P（x，y）在第二象限，且P 到 x 轴、y轴距离分别为３，７，则点P坐标为（　 ）. A、（-3，-7）　　　 B、（-7，3）　　　　 C、（3，7）　　　　　 D、（7，3） B B 想一想 B B 3.点A(-2,-5)到x轴的距离为_____; 到y轴的距离为______.5 2 提高题: 1.若 mn = 0，则点 P（m，n）必定 在 ____上 2.已知点 P（ a，b），Q（3，6）且 PQ ∥ x轴，则 b的值为( ) 3.点（m，- 1）和点（2，n）关于 x 轴对称，则 mn等于【 】 （A）- 2 （B）2 （C）1 （D）- 1 坐标轴 6 B 4.实数 x，y满足 x2+ y2= 0，则点 P（ x，y）在【 】. （A）原点（B）x轴正半轴（C） 第一象限 （D）任意位置 5.点 A 在第一象限，当 m 为何值 （ ）时，点 A（ m + 1，3m - 5）到 x轴的距离是它到 y轴距 离的一半 . A 5 11 小练习: 1）若已知点P（-8，-6），则点p到x轴的距离为 ， 到y轴的距离为 。 2）点A(5,-2) 关于y轴对称点为B,则AB= 。 3) 若已知点P（3a-2，4-a）到x轴的距离等于它到y轴的 距离的2倍,则a为 . 4)如果同一直角坐标系下两个点的横坐标相同，那么过这 两点的直线（ ） （A）平行于 x轴 （B）平行于 y轴（C）经过原点 （D）以上都不对 8 6 10 0 或 7 8 B x y A B CO (1,4) (-4,0) (2,0) 已知A(1,4),B(-4,0),C(2,0). △ABC的面积是＿＿． 1、写出已知坐标的点所在的象限或坐标轴。 ⑴A(-3,0); ⑵B(2,-4)；⑶C(1,2)； ⑷D(-1,-3)；⑸E(0,2)；⑹F(-1.2,+1) 2、写出下列各点关于x轴、y轴、原点对称的点的坐标： ⑴A(1，2); ⑵B(2,-3)；⑶C(-3,-4)；⑷D(-4,5)； 3、在直角坐标系中画出以原点为圆心，5为半径的圆，与 x轴交于A、B两点，与y轴交于C、D两点，并求出A、B、 C、D的坐标。 3.判断下列说法是否正确： （1）（2，3）和（3，2）表示同一点；（ ） （2）坐标轴上的点的横坐标和纵坐标至少有一个为0；（ ） （3）（3，0）是第一象限的点。（ ） （4）如图点A为（-2，3）。（ ） 1、点（-1，2）在（ ） A、第一象限；B、第二象限；C、第三象限；D、第四象限 2、若点（X，Y）在第四象限内，则（ ） A、X，Y同是正数 B、X，Y同是负数 C、X是正数，Y是负数 D、X是负数，Y是正数 B C A 3 -2 • 0 X Y × √ × × 达标测试： 0 1 2 3 4 5-4 -3 -2 -1 3 1 4 2 5 -2 -4 -1 -3 A C（3，-4） B D ∟ 例2、 点M的横坐标是a，纵坐标是b，且a，b 是方程 的两个根，求M点的坐标。 2 8 0x   练习2： 1. 点M（x,y)在第四象限且 ， 求M点的坐标。 4,3  yx 2. 点M（x,y)在第二象限，且x+y=2,请写出两 个符合条件的M点的坐标。 -2 -1 4321-3-4 -4 1 2 3 -3 -1 -2 0 x y 一.三象限角平分线上的点的横坐标与纵坐标相同; 二.四象限角平分线上的点的横坐标与纵坐标相反; 关于x轴对称的点的横坐标相同,纵坐标相反 关于y轴对称的点的纵坐标相同,横坐标相反 关于原点对称的点的横坐标、纵坐标都相反 横坐标相同的点在平行于y轴的同一直线上 纵坐标相同的点在平行于x轴的同一直线上 X轴上的点纵坐标为0 y轴上的点横坐标为0 知识小结