最新人教版七年级数学下册精品课件第五章 相交线与平行线5.3.1 平行线的性质 25页

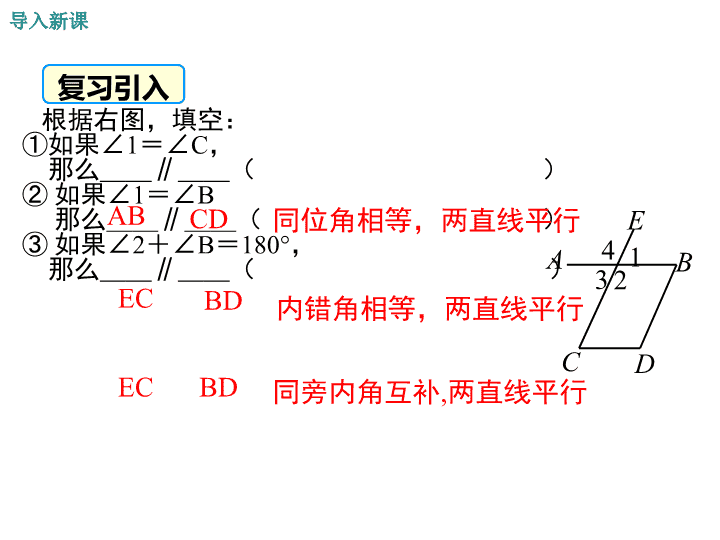
5.3 平行线的性质 第五章 相交线与平行线 导入新课 讲授新课 当堂练习 课堂小结 5.3.1 平行线的性质 第1课时 平行线的性质 学习目标 1.掌握平行线的性质，会运用两条直线是平行关系判 断角相等或互补；（重点） 2.能够根据平行线的性质进行简单的推理. 根据右图，填空： ①如果∠1＝∠C， 　那么＿＿∥＿＿（ 　　　　　 　 ） ② 如果∠1＝∠B 那么＿＿∥＿＿（ 　　 　　 　 ） ③ 如果∠2＋∠B＝180°， 　那么＿＿∥＿＿（ 　　 ） E A C D B1 23 4 AB CD EC BD 同位角相等，两直线平行 内错角相等，两直线平行 EC BD 同旁内角互补,两直线平行 导入新课 复习引入 两直线平行 1.同位角相等 2.内错角相等 3.同旁内角互补 问题 通过上题可知平行线的判定方法是什么？ 思考 反过来,如果两条直线平行,同位角、内错角、 同旁内角各有什么关系呢? 活动 画两条平行线a//b，然后画一条截线c与a、b相交， 标出如图所示的角. 度量所形成的8个角的度数，把结 果填入下表： 角 ∠1 ∠2 ∠3 ∠4 度数 角 ∠5 ∠6 ∠7 ∠8 度数 讲授新课 平行线的性质 b 12a c 56 7 8 3 4 一、平行线的基本性质1 观察 ∠1~ ∠8中，哪些是同位角？它们的度数 之间有什么关系？说出你的猜想： 猜想 两条平行线被第三条直线所截，同位角＿＿＿. 相等 b 12a c 56 7 8 3 4 a b d 再任意画一条截线d，同样度量各个角的度数，你的 猜想还成立吗？ 如果两直线不平行，上述结论还成立吗？ 一般地，平行线具有如下性质： 性质1：两条平行线被第三条直线所截，同位角相等. 简单说成：两直线平行，同位角相等. b 1 2 a c ∴∠1=∠2 （两直线平行，同位角相等） ∵a∥b（已知） 应用格式: 总结归纳 思考：在上一节中，我们利用“同位角相等，两直线 平行线”推出了“内错角相等，两直线平行线”，类 似地，已知两直线平行，同位角相等， 能否得到内错 角之间的数量关系？ 二、平行线的基本性质2 如图，已知a//b,那么 2与 3相等吗？为什么? 解 ∵ a∥b(已知), ∴∠1=∠2(两直线平行,同位角相 等). 又∵ ∠1=∠3(对顶角相等), ∴ ∠2=∠3(等量代换). b 1 2 a c 3 性质2：两条平行线被第三条直线所截，内错角相等. 简单说成：两直线平行，内错角相等. b 1 2 a c 3∴∠2=∠3 （两直线平行，内错角相等） ∵a∥b（已知） 应用格式: 总结归纳 如图,已知a//b,那么 2与 4有什么关系呢？为什 么? b 1 2 a c 4 解: ∵a//b （已知）, ∴ 1= 2 （两直线平行，同位角相等）. ∵ 1+ 4=180° （邻补角的性质）, ∴ 2+ 4=180° （等量代换）. 思考：类似地，已知两直线平行，能否得到同旁内角 之间的数量关系？ 三、平行线的基本性质3 性质3：两条平行线被第三条直线所截，同旁内角互补. 简单说成：两直线平行，同旁内角互补. b 1 2 a c 4 ∴∠2+∠4=180 ° （两直线平行，同旁内角互补） ∵a∥b（已知） 应用格式: 总结归纳 例1 如图是一块梯形铁片的残余部分，量得∠A=100°， ∠B=115°，梯形的另外两个角的度数分别是多少？ A B CD 解：因为梯形上、下底互相平行，所以 ∠A与∠D互补， ∠B与∠C互补. 所以梯形的另外两个角分别是80°、65°. 于是∠D=180 °-∠A=180°-100°=80° ∠C= 180 °-∠B=180°-115°=65° 典例精析 D C E F A A G G 1 2 例2：小明在纸上画了一个∠A，准备用量角器测量它 的度数时，因不小心将纸片撕破，只剩下如图的一部 分，如果不能延长DC、FE的话，你能帮他设计出多少 种方法测出∠A的度数？ 两直线平行 同位角相等 内错角相等 同旁内角互补 平行线的判定 平行线的性质 线的关系 角的关系性质 角的关系线的关系 判定 讨论：平行线三个性质的条件是什么？结论是 什么？它与判定有什么区别？（分组讨论） 四、平行线的判定与性质 素材：探索平行线的性质（播放状态下，点击画面 操作） 探索平行线的性质.swf 1.如图，已知平行线AB、CD被直线AE所截 (1)从 ∠1=110o可以知道∠2 是多少度吗,为什么？ (2)从∠1=110o可以知道 ∠3是多少度吗,为什么？ (3)从 ∠1=110o可以知道∠4 是多少度吗,为什么？ 2 3 E 1 4 A B D C解：(1)∠2=110o ∵两直线平行，内错角相等； （2）∠3=110o ∵两直线平行, 同位角相等； （3）∠4=70o ∵两直线平行,同旁内角互补. 当堂练习 2.如图，一条公路两次拐弯的前后两条路互相平行.第 一次拐弯时∠B是142°，第二次拐弯时∠C是多少 度？ 为什么？ 解：∠C=142o ∵两直线平行,内错角相等. B C 3.如图，直线 a ∥ b,直线b垂直于直线c，那么直线a 垂直于直线c吗? a b c 解： a⊥c . 因为两直线平行, 同位角相等 4.如果有两条直线被第三条直线所截，那么必定有（ ） A.内错角相等 B.同位角相等 C.同旁内角互补 D.以上都不对 D 解: ∵ AB∥DE( 　) ∴∠A=_______ ( ) ∵AC∥DF( ) ∴∠D=______ ( ) ∴∠A=∠D ( ) 5.(1)有这样一道题：如图1,若AB∥DE ,　AC∥DF，试 说明∠A=∠D.请补全下面的解答过程,括号内填写依据. P F C E BA D 图１ 已知 ∠CPE 两直线平行,同位角相等 已知 ∠CPE 两直线平行,同位角相等 等量代换 解: ∵ AB∥DE( 　) ∴∠A= ______ ( ) ∵AC∥DF( ) ∴∠D+ _______=180o ( ) ∴∠A+∠D=180o（ ） 5.(2)有这样一道题：如图2,若AB∥DE ,　AC∥DF， 试说明∠A+∠D=180o.请补全下面的解答过程,括号 内填写依据. 图2 F C E B A D P 已知 ∠CPD 两直线平行,同位角相等 已知 ∠CPD 两直线平行,同旁内角互补 等量代换 思维拓展：如图，潜望镜中的两面镜子是互相平 行放置的，光线经过镜子反射时，∠1=∠2， ∠3=∠4，∠2和∠3有什么关系？为什么进入潜望 镜的光线和离开潜望镜的光线是平行的？ 解：∠2=∠3， ∵两直线行，内错角相等； ∵∠1=∠2=∠3=∠4， ∴ ∠5=∠6， ∴进入潜望镜的光线和 离开潜望镜的光线平行. 同位角相等 内错角相等 同旁内角互补 两直线平行 判定 性质 已知 得到 得到 已知 课堂小结