北师版七年级数学上册第一章《丰富的图形世界》　综合能力检测卷（Word版附答案） 9页

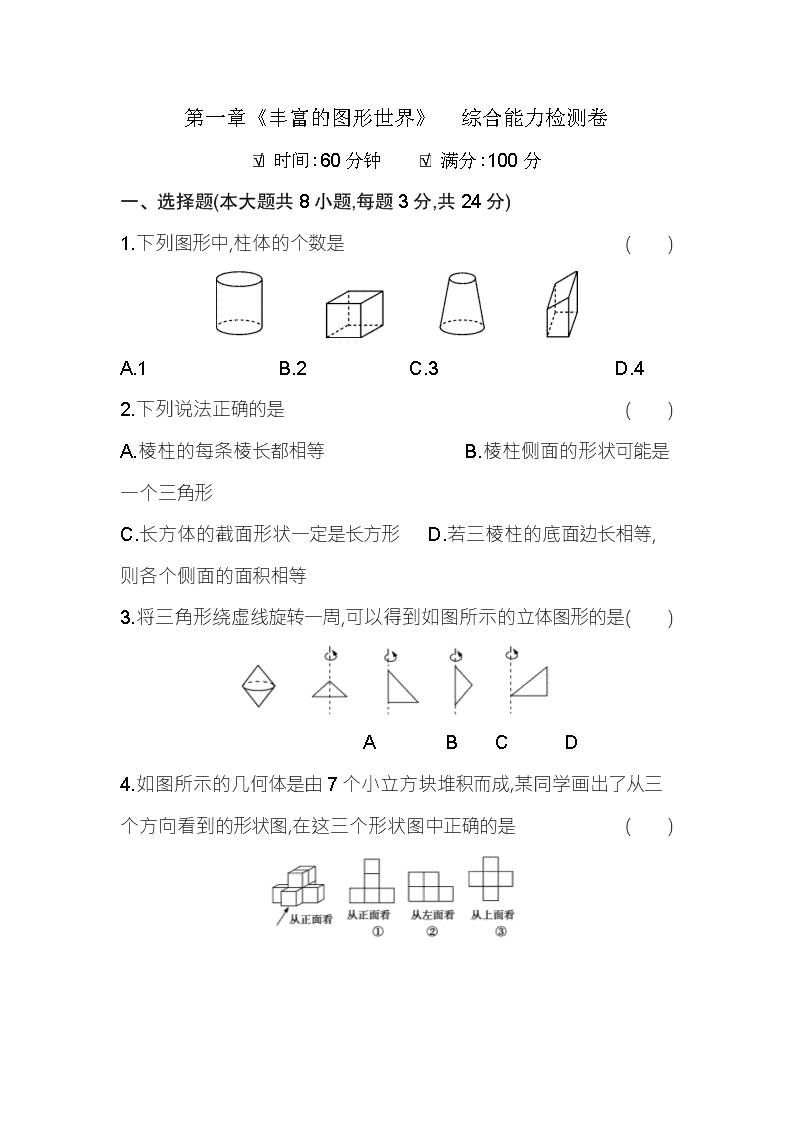
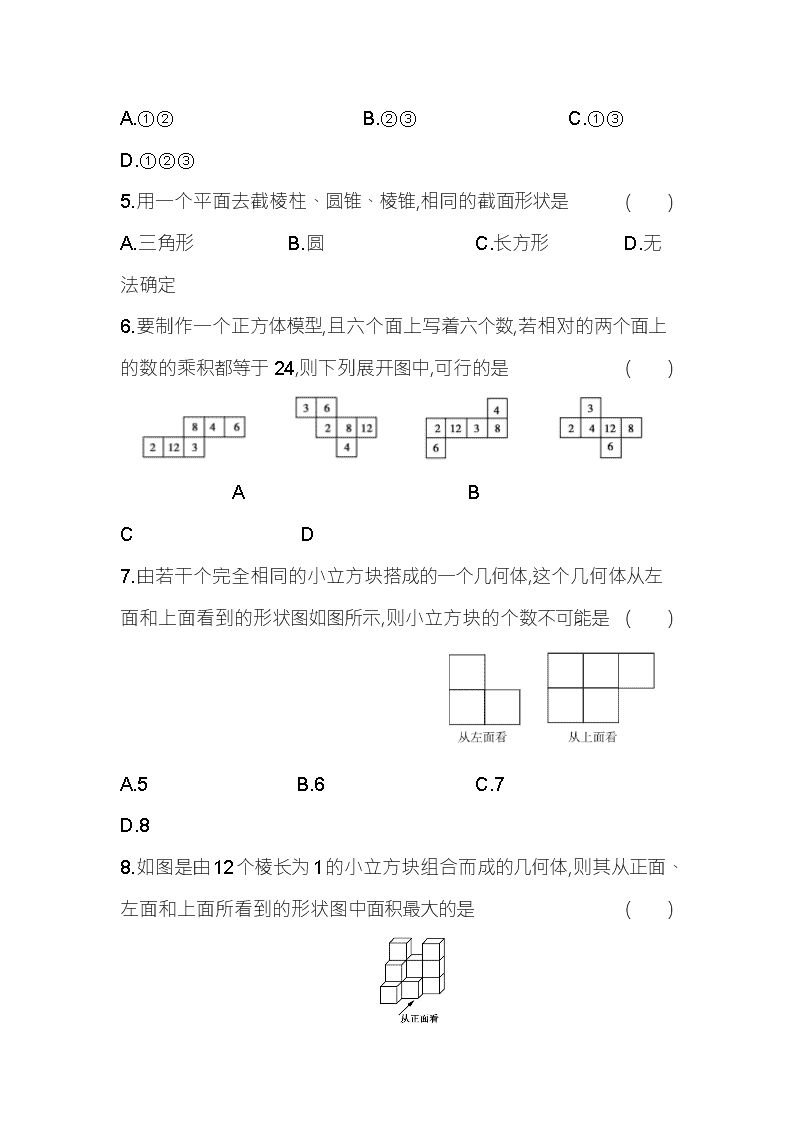
第一章《丰富的图形世界》　综合能力检测卷 ‎ 时间:60分钟　　 满分:100分 一、选择题(本大题共8小题,每题3分,共24分)‎ ‎1.下列图形中,柱体的个数是(　　)‎ A.1 B.2 C.3 D.4‎ ‎2.下列说法正确的是(　　)‎ A.棱柱的每条棱长都相等 B.棱柱侧面的形状可能是一个三角形 C.长方体的截面形状一定是长方形 D.若三棱柱的底面边长相等,则各个侧面的面积相等 ‎3.将三角形绕虚线旋转一周,可以得到如图所示的立体图形的是(　　)‎ ‎　　　　　　　　　　　 　A　 　 B　　C　　　D ‎4.如图所示的几何体是由7个小立方块堆积而成,某同学画出了从三个方向看到的形状图,在这三个形状图中正确的是(　　)‎ A.①② B.②③ C.①③ D.①②③‎ ‎5.用一个平面去截棱柱、圆锥、棱锥,相同的截面形状是(　　)‎ A.三角形 B.圆 C.长方形 D.无法确定 ‎6.要制作一个正方体模型,且六个面上写着六个数,若相对的两个面上的数的乘积都等于24,则下列展开图中,可行的是(　　)‎ ‎　　　　　　A　　　　　　　　　　　　B　　　　　　　　　　C　　　　　　　　　D ‎7.由若干个完全相同的小立方块搭成的一个几何体,这个几何体从左面和上面看到的形状图如图所示,则小立方块的个数不可能是(　　)‎ A.5 B.6 C.7 D.8‎ ‎8.如图是由12个棱长为1的小立方块组合而成的几何体,则其从正面、左面和上面所看到的形状图中面积最大的是(　　)‎ ‎ ‎ A.从正面看到的形状图 B.从左面看到的形状图 C.从上面看到的形状图 D.无法判断 ‎ 二、填空题(本大题共6小题,每题3分,共18分)‎ ‎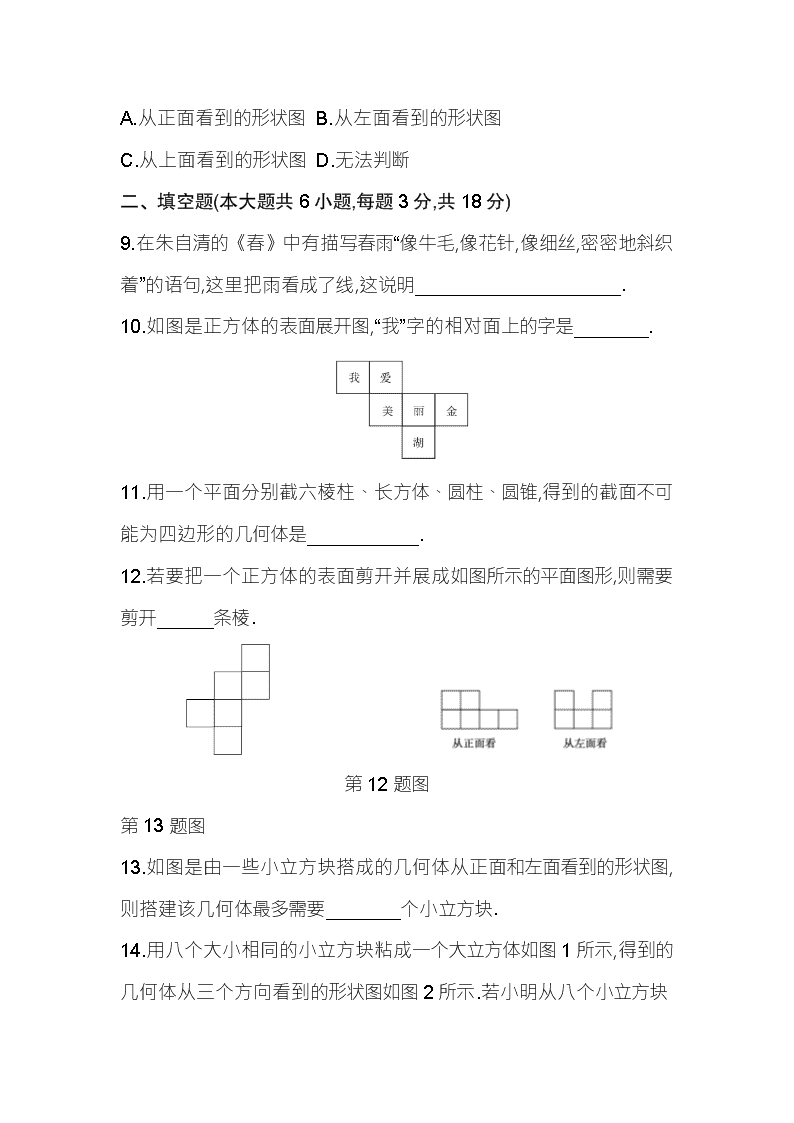9.在朱自清的《春》中有描写春雨“像牛毛,像花针,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明　　　　　　　　　　　. ‎ ‎10.如图是正方体的表面展开图,“我”字的相对面上的字是　　　　. ‎ ‎11.用一个平面分别截六棱柱、长方体、圆柱、圆锥,得到的截面不可能为四边形的几何体是　　　　　　. ‎ ‎12.若要把一个正方体的表面剪开并展成如图所示的平面图形,则需要剪开　　　条棱. ‎ ‎ ‎ ‎　　　　　　　　　　　　第12题图　　　　　　　　　　　　　　第13题图 ‎13.如图是由一些小立方块搭成的几何体从正面和左面看到的形状图,则搭建该几何体最多需要　　　　个小立方块. ‎ ‎14.用八个大小相同的小立方块粘成一个大立方体如图1所示,得到的几何体从三个方向看到的形状图如图2所示.若小明从八个小立方块 中取走若干个,剩余的小立方块保持原位置不动,并使得到的新几何体从三个方向看到的形状图仍是图2,则他取走的小立方块最多可以是　　　　个. ‎ ‎　　　　　　　　　　　　　　　　图1　　　　　　　　　　　图2‎ 三、解答题(本大题共6小题,共58分)‎ ‎15.(6分)如图所示是一个几何体,画出从正面、左面、上面看到的该几何体的形状图.‎ ‎16.(10分)如图是一个长为4 cm,宽为3 cm的长方形纸片.‎ ‎　　　　　　　　　　　　　　　　　　　　　　 　图1　　 　图2‎ ‎(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是　　　　,这能说明的事实是　　　　　　　　　　; ‎ ‎(2)求当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积;‎ ‎(3)求当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.‎ ‎17.(10分)有一种牛奶包装盒及其尺寸如图1所示.为了生产这种包装盒,需要先画出展开图纸样.‎ 图1‎ 图2‎ ‎(1)如图2所示,给出3种纸样甲、乙、丙,在甲、乙、丙中,正确的是　　　　; ‎ ‎(2)从已知正确的纸样中选出一种,在图上标注上尺寸;‎ ‎(3)利用你所选的一种纸样,求出包装盒的表面积.‎ ‎18.(10分)设棱锥的顶点数为V,面数为F,棱数为E.‎ ‎(1)观察与发现:如图,三棱锥中,V3=　　　　,F3=　　　　,E3=　　　　; ‎ 五棱锥中,V5=　　　　,F5=　　　　,E5=　　　　. ‎ ‎(2)猜想:①十棱锥中,V10=　　　　,F10=　　　　,E10=　　　　; ‎ ‎②N棱锥中,Vn=　　　　,Fn=　　　　,En=　　　　.(用含有n的式子表示) ‎ ‎(3)探究:①棱锥的顶点数(V)与面数(F)之间的等量关系:　　　　; ‎ ‎②棱锥的顶点数(V)、面数(F)、棱数(E)之间的等量关系:　　　　. ‎ ‎(4)拓展:棱柱的顶点数(V)、面数(F)、棱数(E)之间是否也存在某种等量关系?若存在,试写出相应的等式;若不存在,请说明理由.‎ ‎19.(10分)用小立方块搭一个几何体,使得它从正面和上面看到的形状图如图所示,则搭这个几何体最少要多少个小立方块?并画出此时该几何体从左面看到的形状图(只需画出一种情况即可).‎ ‎20.(12分)在平整的地面上,由若干个完全相同的棱长为10 cm的小立方块堆成一个几何体,如图所示.‎ ‎(1)这个几何体由多少个小立方块组成?请画出从正面、左面、上面看到的这个几何体的形状图.‎ ‎(2)如果在这个几何体的表面(不包括底面)喷上黄色的漆,则在所有的小立方块中,有多少个只有一个面是黄色?有多少个只有两个面是黄色?有多少个只有三个面是黄色?‎ ‎(3)假设现在你手里还有一些相同的小立方块,保持从左面、上面看到的形状图不变,最多可以再添加几个小立方块?这时如果要重新给这个几何体表面(不包括底面)喷上红色的漆,需要喷漆的面积比原几何体增加了还是减少了?增加或减少的面积是多少?‎ 第一章　综合能力检测卷 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C D C B A B A A ‎9.点动成线　10.丽　11.圆锥　12.7　13.16　14.4‎ ‎17. (1)甲、丙 ‎(2)如图所示,任选其一即可.‎ ‎(3) 288.‎ ‎18. (1)4　4　6　6　6　10‎ ‎(2)①11　11　20　②n+1　n+1　2n ‎(3)①V=F　②V+F-E=2‎ ‎(4)存在,相应的等式为V+F-E=2.‎ ‎19.‎ 最少需要12个小立方块.‎ 此时该几何体从左面看到的形状图如图所示.‎ ‎20. (1) 10个 从正面、左面、上面看到的这个几何体的形状图如图所示.‎ ‎(2)略 ‎ (3)最多可以再添加4个小立方块.‎ ‎400cm2‎