华师大版七年级数学上教学课件：最基本的图形-点和线 28页

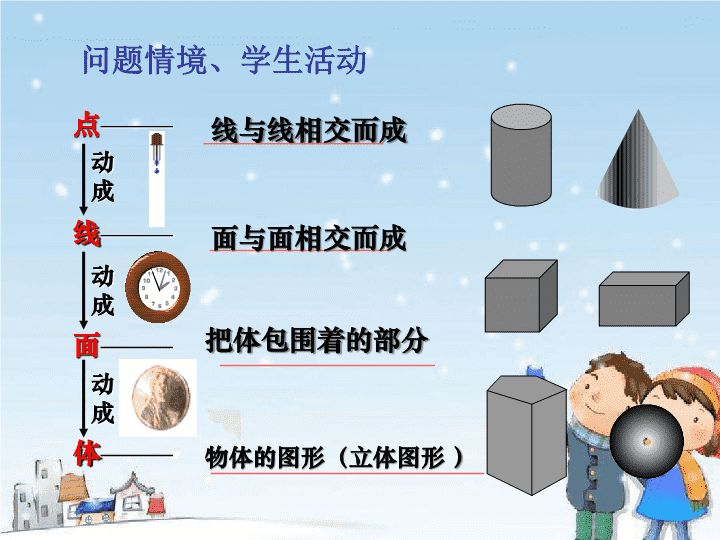
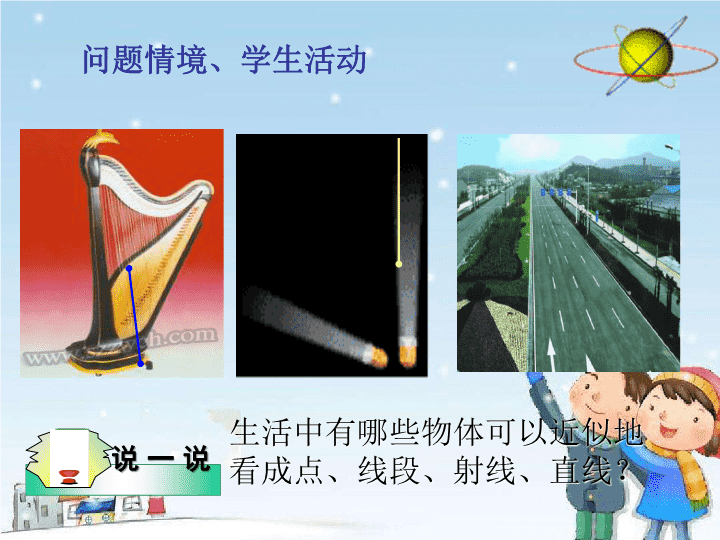
4.5 最基本的图形 — 点和线 问题情境、学生活动 动 成 动 成 动 成 点 ——— 线与线相交而成 线 ——— 面 ——— 面与面相交而成 把体包围着的部分 体 ——— 物体的图形（立体图形 ） 问题情境、学生活动 生活中有哪些物体可以近似地 看成点、线段、射线、直线？ 说 一 说 数学理论  ：  ： 线段的表示法有： 用大写的 ( 端点 ) 两个字母 线段 AB A B 用小写的一个字母 a 线段 a 线段 BA 射线的表示法： ： 用大写的两个字母 射线 ； 射线 ； ( 其中一个在端点， C D 另一个在线上任取一点 .) E F CE DF 直线的表示法：  ：  ： 用大写的 ( 内部 ) 两个字母 直线 ； 直线 ； A B AB BA 用小写的一个字母 ( 标在所画直线的一旁 . ) a 直线 a ① 表示端点的字母写在首位；② 两个字母不能调换位置 . 在射线的表示法中，要注意两点： 数学理论 直线、射线、线段有什么区别与联系 线 段 射 线 直 线 端 点 度 量 延伸性 关 系 两 个 一 个 零 个 可 以 不 能 不 能 不能无限延伸 向一个方向无限延伸 向两个方向无限延伸 把线段向一方无限延长 把线段向两方无限延长 直线上两点间部分 直线上一点一旁部分 问题情境、学生活动 指出下图中线段、射线、直线分别有多少条？ A B C 有 6 条射线 . 只有一条直线，是直线 AB . 有 3 条线段线段 AB , 线段 AC , 线段 BC . 答 : 点 A , 点 B , 点 C 在直线 AB 上 . 直线 AB 过点 A , 点 B , 点 C . 点 A , B , C 三点共线 . 问题情境、学生活动 指出下图中线段、射线、直线分别有多少条？ A B C 有 4 条射线 . 只有一条直线，是直线 AB . 有 6 条线段 . 答 : D 思考：若直线上有 n 个点，则有多少条线段，多少条射线？ 问题情境、学生活动 两只非洲豹 同时、同地、同速 , 扑向猎物，到达的时间 却不一样 为什么 ? 结论 : 两点间线段最短 生活中运用 “两点间线段最短”的事例，你能列举吗？ 数学理论 线段公理 : 两点之间 , 线段最短 连结两点所得线段的长度叫做这两点间的距离 . A Ｂ 长度 长度 距离 距离 问题情境、学生活动 1. 过一点 A 画一条直线， 请问可以画几条 ? 2. 过两点 A , B 可以画几条直线？ 请动手试一试 . (1) 用一枚图钉把一条硬纸条 钉在书上 , 纸条还能动吗 ? (2) 钉几枚图钉才能使硬纸条 保持不动 ? 最少钉几枚 ? (3) 由此你可以总结出什么样 的数学事实 ? 过一点 A 可以画无数条直线  画一画  · A 数学理论 直线的基本性质： 经过两点有一条直线，并且只有一条直线 . 简述为： 过两点有且只有一条直线 . 或简述为： 两点确定一条直线 . A Ｂ 数学运用 1. 在下面的图中，你能说出点 E 、 F 、 G 分别和直线 a 、 b 的位置关系吗 ? 2 . 如上图，直线 a 与直线 b 相交于 ______. 也就是说，直线 AB 、 CD 都经过 _____. a 点 E 在直线 a 上 , 也在直线 b 上 ; E F G b 答 : 点 F 在直线 a 上 , 在直线 b 外 ; 点 G 在直线 a 外 , 也在直线 b 外 . 点 E 点 E 拓展提高 过同一平面上的三个点中的任两个点 , 可以画几条直线 ? ( 1 ) 可以画三条直线 ( 2 ) 只能画一条直线 过同一平面上的四个点中的任两个点 , 可以画几条直线 ? 可以画一或四或六条直线 图案欣赏 挑战： 你能用线段、 射线或直线 创造出美丽 的图案吗？ 问题情境、学生活动 你们平时是如何比较两个同学的身高的？你能从比身高的方法中得到启示来比较两条线段的长短吗？讨论后派一位代表上来说说你们的想法 . 数学理论 线段的比较： 第一种方法是：度量法，即用一把尺量出两 条线段的长度，再进行比较 . 1 2 3 5 4 6 7 8 0 3.1 cm 4.1 cm 1 2 3 5 4 6 7 8 0 数学理论 第二种方法是：叠合法先把两条线段的一端 重合，另一端落在同侧，根据另一端落下的 位置，来比较 . ① ② ③ A B B A A B C D E F M N AB ＞ CD AB = EF AB ＜ MN 数学运用 观察下列三组图形，分别比较线段 a , b 的长短 . （ 1 ） a b （ 3 ） （ 2 ） a b a b 数学运用 现有一个三边分别为 a ， b ， c 的三角形，不 用刻度尺你能否比较它们的大小？ a b c a b 数学运用 现有一个三边分别为 a ， b ， c 的三角形，不 用刻度尺你能否比较他们的大小？ a b b c 数学运用 画在黑板上的两条线段是无法移动的，在没 有度量工具的情况下，请大家想想办法，如 何来比较它们的长短？ ① 观察法 ② 借助于某一物体，如铅笔、小木棒等 可用圆规？ 数学运用 已知线段 a （如图所示），用直尺和圆规 画出一条线段，使它等于已知线段 a . a 画法： 1 . 任意画一条射线 AC . 2 . 用圆规量取已知线段 a 的长度． 3 . 在射线 AC 上截取 AB = a . A C B ∴ 线段 AB 就是所求的线段 a . a 数学理论 定义 把一条线段分成两条相等线段的点 , 叫做这条线段的 中点 . B C A D 线段 AC 的中点 B C A 数量关系 : AB + BC = AC AB = BC = AC 1 2 你记住什么是线段的中点了吗？ 如上图 , 若 AB =2 cm , 则线段 AC = cm , 线段 BC = cm 4 2 AC =2 AB =2 BC 数学运用 概念辨析： “若 AC ＝ BC ，则点 C 是线段 AB 的中点”这种说 法对吗？ 小王的解答是这样的： 解：如图 : ∵ AC ＝ BC ， ∴ AB ＝ 2 AC ，∴点 C 是 AB 的中点 你认为小王的解答全面吗？ 如果不全，漏了哪些情况？ 答 : 不全面 . 漏了两种情况 . （点 C 在 AB 的延长线上；或不在直线 AB 上 . ） A C B 数学运用 例 1 如图①， AD ＝ AB － 　　 ＝ AC ＋ 　　 。 例 2 如图②，下列说法不能判断点 C 是线段 AB 的中点的是（　　　） （ A ） AC ＝ CB 　　　　　（ B ） AB ＝ 2 AC （ C ） AC ＋ CB ＝ AB 　　　（ D ） 2 CB ＝ AB 图① 图② DB CD C C B A 数学运用 例 3 AB ＝ 6 cm , 点 C 是线段 AB 的中点，点 D 是线段 CB 的中点 , 求线段 AD 的长 . B C A D 解 : AC = BC = AB =3cm 1 2 CD = CB = 1.5cm 1 2 AD = AC + CD =4.5cm 答：线段 AD 的长等于 4.5cm. 数学运用 例 4 在一条直线上顺次取 A 、 B 、 C 三点，使 AB =5 cm ， BC =2 cm ，并且取线段 AC 的中点 O ， 求线段 OB 的长 . A B C O 解： AC = AB + BC =5+2=7cm AO = OC = AC =3.5cm 1 2 OB = AB - AO =5-3.5=1.5cm （或 OB = OC - BC =3.5-2=1.5cm ） 答：线段 OB 的长等于 1.5 cm. 回顾反思 这节课你学会了什么？ 如何比较两条线段的大小 . 学会画一条线段等于已知线段 . 了解两条线段的和与差仍是线段 . 学会线段的中点定义及相关计算 .