七年级数学下册第6章一元一次方程6-3实践与探索第1课时教学课件华东师大版 21页

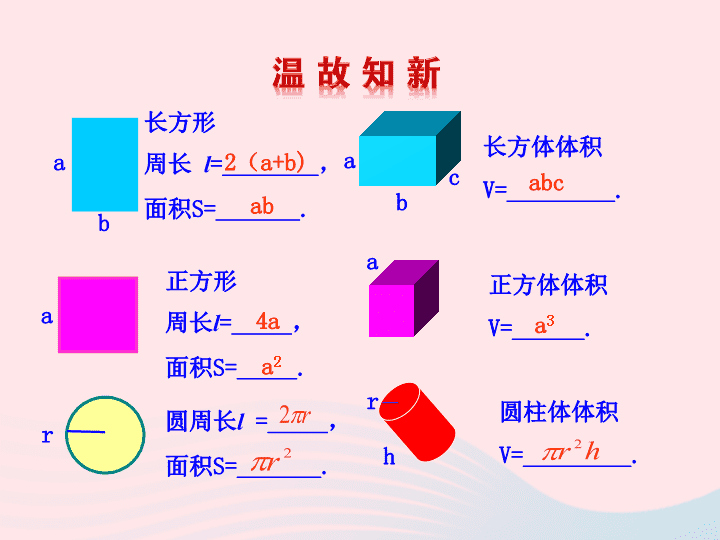
6.3 实践与探索 第1课时 1. 掌握用一元一次方程解决实际问题的步骤． 2. 熟练用一元一次方程解决生活中的等积变形问题和利 率问题 . 3. 培养将生活实际问题转化成数学问题的能力 . 长方形 周长 l =________ ， 面积 S=_______. 正方形 周长 l =_____ ， 面积 S=_____. 圆周长 l =_____ ， 面积 S=_______. a b a r 2 （ a+b) ab 4a a 2 b a c a r h 长方体体积 V=_________. 正方体体积 V=______. 圆柱体体积 V=_________. abc a 3 加工 思考：在加工过程中只 是发生了什么变化，而 没有变化的是什么？ 钢铁工人正在锻造车间工作 【 例 1】 将一个底面直径是 10 厘米，高为 36 厘米的“瘦长” 形圆柱锻压成底面直径是 20 厘米的“矮胖”形圆柱，高变 成了多少？ 【 分析 】 设锻压后圆柱的高为 x 厘米，填写下表： 锻压前 锻压后 底面半径 高 体积 加工 特点：等积变形 【 例题 】 【 解析 】 设锻压后圆柱的高为 x 厘米， 根据等量关系，列出方程： 解得 答：高变成了 9 厘米 . 关键：等积变形 加工 小明要用一根长 10 米的铁丝围成一个长方形，他想使得长 方形的长比宽多 1.4 米，此时长方形的长、宽各为多少 米？面积呢？ 【 解析 】 设此时长方形的宽为 x 米， x 则它的长为（ x+1.4) 米 . x+1.4 根据题意，得 答：长方形的长为 3.2 米，宽为 1.8 米；面积为 5.76 平方米 . 【 跟踪训练 】 学以致用 本金、利息、本息、期数、利率的概念 顾客存入银行的钱叫本金 银行付给顾客的酬金叫利息 本息和 = 本金 + 利息 利息 = 本金 × 利率 × 期数 知识储备 【 例 2】 为了准备小颖 6 年后上大学的 5 000 元费用，她的 父母现在就参加了教育储蓄 . 下面有两种储蓄方式： （ 1 ）直接存入一个 6 年期年利率为 2.88% ； （ 2 ）先存一个 3 年期的， 3 年后将本息和自动转存一个 3 年 期年利率为 2.7%. 你认为那种储蓄方式开始存入的本金少？ 【 例题 】 【 解析 】 设开始存入 x 元 , 列出方程得 （ 1+2.88%×6 ） x=5 000 解得 x≈4263.3 （ 1 ＋ 2.7%×3 ） · x · （ 1 ＋ 2.7%×3 ） =5000 ， 1.168561x=5000 ， x≈4278.8. 方案一： 方案二： 4263.3<4278.8. 答：方案一存入钱少一些 . 2.88 六年 2.70 三年 2.25 一年 教育储蓄利率 % 【 解析 】 1000+1000×2.70%×3=1081 （元） 或： 1000× （ 1 ＋ 2.70%×3 ） =1081 （元） 1. 小颖的父母给她存了一个 三年期的教育储蓄，起初存入 1 000 元 . 那么三年后能取出多 少钱？ 【 跟踪训练 】 2.88 六年 2.70 三年 2.25 一年 教育储蓄利率 % 【 解析 】 设开始存入 x 元 , 列 出方程： （ 1+2.70%×3 ） x=5 000 解得 x≈4 625.3. 答：本金是 4 625.3 元 . 2. 如果小颖的父母三年后取出 了 5 000 元钱，你能求出本金 是多少吗？ 【 解析 】 由题意得 0.5a+(100 － a)×0.5×(1+20%)=56, 解得 a=40. 答案： 40 1. （潼南 · 中考）某地居民生活用电基本价格为 0.50 元 / 度 . 规定每月基本用电量为 a 度 , 超过部分用电量的毎度电价比基 本用电量的毎度电价增加 20% 收费 , 某用户在 5 月份用电 100 度 , 共交电费 56 元 , 则 a= 度 . 2. （聊城 · 中考） 2008 年全国废水（含工业废水和城镇生活污 水）排放总量约为 572 亿吨，排放达标率约为 72% ，其中工业废 水排放达标率约为 92% ，城镇生活污水排放达标率约为 57%. 这一 年全国工业废水与城镇生活污水的排放量分别是多少亿吨？ （结果精确到 1 亿吨）（注：废水排放达标率是指废水排放达标 量占总量的百分比） 【 解析 】 设 2008 年全国工业废水的排放量是 x 亿吨，由题意得 92%x+ （ 572-x ） ×57%=572×72%. 解得， x≈245 ，所以 572-x=327. 即这一年全国工业废水与城镇生活污水的排放量分别约是 245 亿吨、 327 亿吨 . 3. 某企业向银行申请了甲、乙两种贷款，共 35 万元，每年 需付利息 2.25 万元，甲种贷款每年的利率是 7% ，乙种贷款 每年的利率是 6% ，求甲、乙两种贷款的数额分别是多少？ 【 解析 】 设甲种贷款 x 万元，则乙种贷款（ 35 － x ）万元， 根据题意列方程得 7% · x ＋（ 35 － x ） · 6%=2.25 ， 解得 x=15 ， 35 － x=20. 答：甲种贷款的数额是 15 万元，乙种贷款的数额是 20 万元 . 4. （晋江 · 中考） 2010 年春季我国西南大旱，导致大量农 田减产，下面是一对农民父子的对话内容，请根据对话内 容分别求出该农户今年两块农田的花生产量分别是多少千 克？ 父：咱家两块农田去年花生产量一共是 470 千克，可老天 不作美，四处大旱，今年两块农田只产花生 57 千克 . 子：今年，第一块田的产量比去年减产 80% ，第二块田的 产量比去年减产 90%. 【 解析 】 设去年第一块田的花生产量为 x 千克，则去年第 二块田的花生产量为（ 470-x ）千克，根据题意，得（ 1- 80% ） x+(1-90%)(470-x)=57 ，解得 x=100 ， 所以（ 1-80% ） x= （ 1-80% ） ×100=20 ， (1-90%)(470-x)= (1-90%)× （ 470-100 ） =37. 答：该农户今年第一块农田的花生产量是 20 千克，第二块 农田的花生产量是 37 千克 . 5. 有一底面半径为 5 cm 的圆柱形储油器，油液中浸有钢 珠，若从中捞出 468π 克钢珠，则液面下降多少厘米？ （ 1 立方厘米钢珠 7.8 克） 【 解析 】 设液面下降 x 厘米，根据题意，得 π · 5 2 · x= 解得， x= 答：液面下降 厘米 . 通过本课时的学习，需要我们掌握： 在分析实际问题中复杂的数量关系时，可借 助表格、图形帮助审题，准确地分析题意，探索 已知量和未知量之间的数量关系，找出题中的等 量关系，通过列一元一次方程解决实际问题 . 没有伟大的意志力，便没有雄才大略 .