七年级上册数学同步练习4-1-1 第2课时 从不同的方向看立体图形和立体图形的展开图 人教版 4页

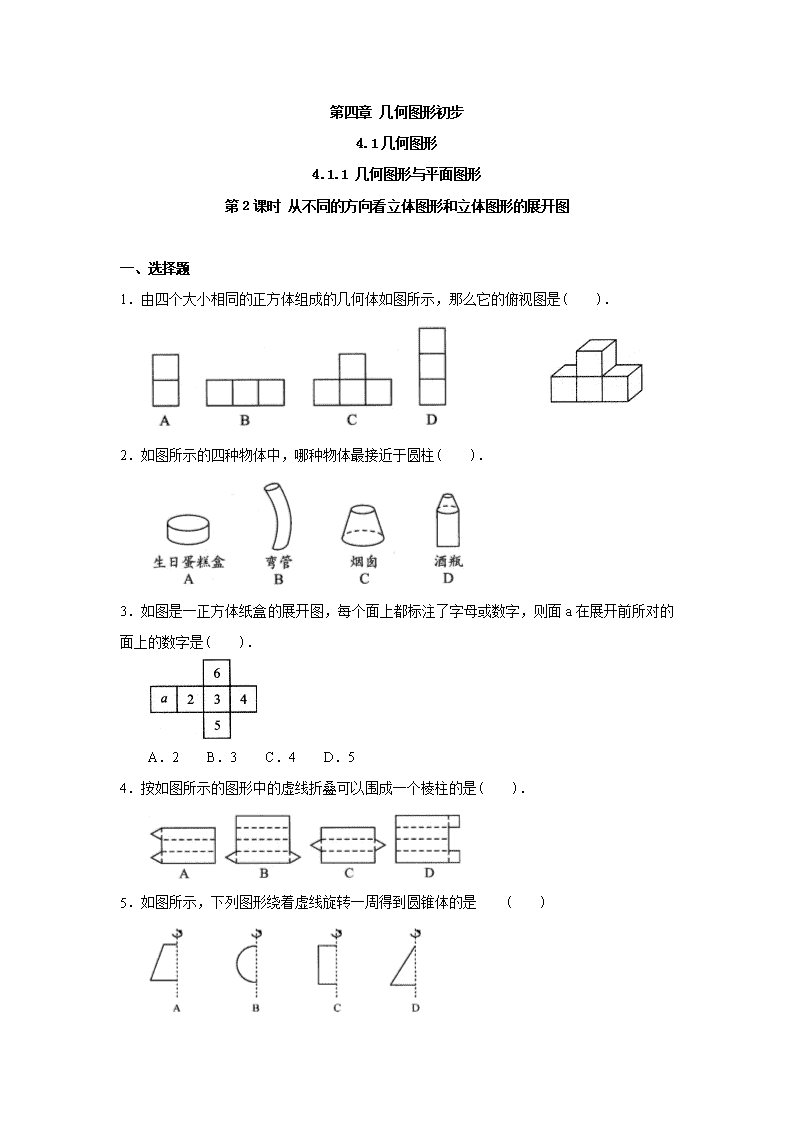
第四章 几何图形初步 ‎4.1几何图形 ‎4.1.1 几何图形与平面图形 第2课时 从不同的方向看立体图形和立体图形的展开图 一、选择题 ‎1．由四个大小相同的正方体组成的几何体如图所示，那么它的俯视图是( )．‎ ‎2．如图所示的四种物体中，哪种物体最接近于圆柱( )．‎ ‎3．如图是一正方体纸盒的展开图，每个面上都标注了字母或数字，则面a在展开前所对的面上的数字是( )．‎ ‎ A．2 B．3 C．4 D．5‎ ‎4．按如图所示的图形中的虚线折叠可以围成一个棱柱的是( )．‎ ‎ ‎ ‎5．如图所示，下列图形绕着虚线旋转一周得到圆锥体的是 ( )‎ ‎ ‎ ‎6．将左图中的正方体纸盒沿所示的粗线剪开，其平面展开图的示意图为（　　）‎ A. B. C. D. ‎ 二、填空题 ‎7．五棱柱有________个顶点，________条棱，________个面．‎ ‎8．柱体包括________和________，锥体包括________和________．‎ ‎9．一个正方体的每个面都写有一个汉字，其平面展开图如图所示，那么在该正方体中，和“超”相对的字是________．‎ ‎10．(内蒙古赤峰)如图所示是一个几何体的三视图，则这个几何体是________．‎ ‎11．圆锥的底面是__________形，侧面是__________的面，侧面展开图是__________形.‎ ‎12．当笔尖在纸上移动时，形成_______，这说明：_____；表针旋转时，形成了一个 ，这说明： ；长方形纸片绕它的一边旋转，形成的几何图形就是 ，这说明： .‎ 三、解答题 ‎13. 如图所示是一个长方体的展开图，每个面上都标注了字母，请根据要求回答问题：‎ ‎(1)如果面A在多面体的上面，那么哪一面会在下面?‎ ‎(2)如果面F在多面体的后面，从左面看是面B，那么哪一面会在上面?‎ ‎(3)从右面看是面A，从上面看是面E，那么哪一面会在前面?‎ ‎14．如图所示是一个机器零件从正面看和从上面看所得到的图形，求该零件的体积(取3.14，单位：mm)(提示：底面积×高)．‎ ‎15. 如图所示的一张硬纸片，它能否折成一个长方体盒子？若能，说明理由，并画出它的立体图形，计算它的体积．‎ 参考答案 一、选择题 ‎1.B； 2.A； ‎ ‎3.B；【解析】‎ 要求面a在展开前所对的面上的数字，我们可以把正方体的展开图折叠起来，则面a、2、3、4按照第一、三个对应，第二、四个对应，于是面a在展开前所对的面上的数字为3．‎ ‎4. C ；【解析】A、D中两个底面不能放在同一侧，B中侧面个数与底面边数不等，故选C． ‎ ‎5. D ；【解析】选项A、B、C、D中的图形旋转一周分别形成圆台、球、圆柱和圆锥，故选D．‎ ‎6. C；【解析】由正方体的表面展开图的特点再结合实际操作，便可得解． ‎ 二、填空题 ‎7. 10， 15， 7 ；【解析】五棱柱上底面有5个顶点，下底面有5个顶点，共10个顶点；上、下底面各有5条棱，竖直有5条棱，共15条棱；7个面，其中5个侧面，2个底面．‎ ‎8. 圆柱，棱柱； 圆锥，棱锥 ‎9. 自；【解析】要弄清立体图形与其平面展开图各部分间的关系，需要较强的空间想象能力，这种能力是建立在动手操作、认真观察与善于思考的基础上．‎ ‎10.三棱柱(或填正三棱柱) ；【解析】考查空间想象能力．‎ ‎11.圆，曲，扇 ；【解析】动手操作或空间想象，便得答案．‎ ‎12.一条线，点动成线；圆面，线动成面；圆柱体，面动成体 ‎ 三、解答题 ‎13.解：(1)如果面A在多面体的上面，那么面C会在下面．‎ ‎ (2)如果面，在多面体的后面，从左面看是面C，那么向外折时面C会在上面，向里折时面A会在上面．‎ ‎(3)从右面看是面A，从上面看是面E，那么向外折时从前面看是面B，向里折时从前面看是面D．‎ ‎14．解：(mm3)，‎ 即该零件的体积为40048 mm3．‎ 提示：由该零件从正面看和从上面看所得到的图形可以确定该零件是由上、下两部分组成的，上面是一个高为32 mm，底面直径为20 mm的圆柱；下面是一个长为30 mm，宽为25 mm，高为40 mm的长方体，零件的体积是圆柱与长方体体积之和．‎ ‎15. 【解析】‎ 解：能折成一个长方体盒子，因为符合长方体的平面展开图的所有条件，该几何体的立体图形如图所示．此长方体的长为5m，宽为2m，高为3m，所以它的体积为：‎ ‎5×2×3＝30(m3)．‎ ‎ ‎