八年级下数学课件：19-1-2 函数的图象 （共15张PPT）_人教新课标 15页

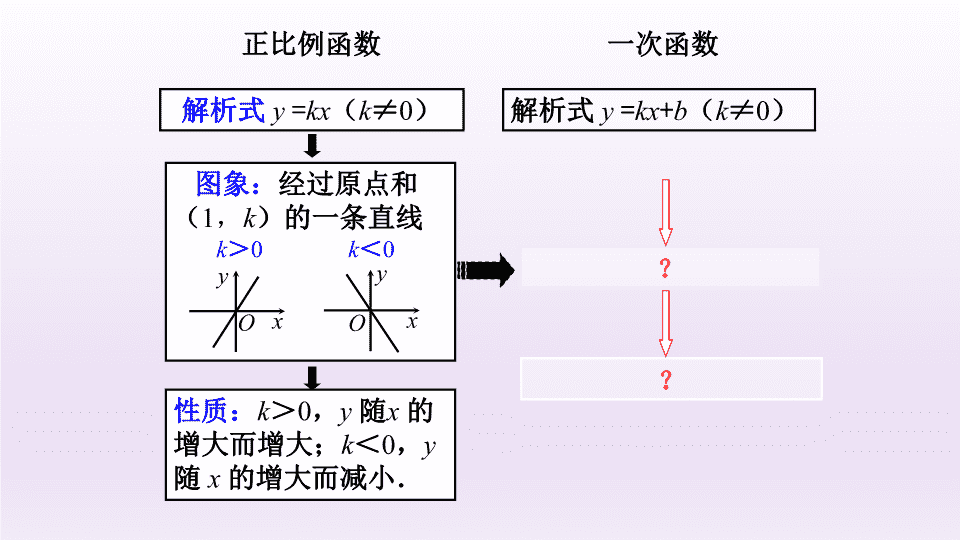
一次函数图像与性质 问题情境（1）什么是正比例函数、一次函数？它们之间有什么联系？（2）正比例函数的图像是什么样的？（3）正比例函数y=kx(k是常数，k≠0)中，k的正负对函数的图像有什么影响？我们是如何研究它的？活动1问题 正比例函数解析式y=kx（k≠0）图象：经过原点和（1，k）的一条直线xyOk＞0k＜0xyO性质：k＞0，y随x的增大而增大；k＜0，y随x的增大而减小．一次函数解析式y=kx+b（k≠0）？？ 活动2问题1、画图，用描点法在同一坐标系中画出函数y=2x,y=2x+1的图像。观察：比较上面两个函数图像的相同点和不同点，根据你的观察结果回答下列问题：（1）这两个函数图像的形状都是＿＿＿＿＿，并且倾斜程度都＿＿＿＿＿，它们的位置＿＿＿＿＿；（2）函数y=2x的图像经过原点，函数y=2x+1的图像与y轴交于点＿＿＿＿＿，即可以看作由直线y=2x向＿平移＿＿个单位长度而得到；（3）比较两个函数的解析式，试由此解释两个函数图像的位置关系。1上（0,1）平行相同直线 2、拓展延伸（1）联系上面的结果考虑一次函数y=kx+b（k≠0）的图像是什么形状，它与直线y=kx（k≠0）有什么关系？结论：一次函数y=kx+b（k≠0）的图像可以由直线y=kx平移︱b︱个单位长度得到（当b〉0时，向上平移；当b〈0时，向下平移）.一次函数y=kx+b（k≠0）的图像也是一条直线，我们称它为直线y=kx+b 活动3问题在刚才画好的坐标系中画出函数y=-2x+1，y=x+1与y=-x+1的图像怎样快速画出函数图像呢？方法指导：两点法画一次函数y=kx+b（k,b是常数，k≠0）的图像，通常取直线y=kx+b与x轴的交点＿＿＿＿和与y轴的交点＿＿＿＿（0，b）（,0） 活动4探究1、探究：观察坐标系中函数y=x+1,y=2x+1,y=-x+1,y=-2x+1的图像.由它们联想：一次函数解析式y=kx+b（k,b是常数，k≠0）中，k的正负对函数图像有什么影响？性质：k＞0时，k＜0时，y随x的增大而增大；y随x的增大而减小； 规律方法总结：我们先通过画图像观察图像（形）得出规律，再根据这些规律得到一次函数解析式y=kx+b（k≠0）（数）的性质，这种数形结合的研究方法在数学学习中很重要。 活动5小试身手1、直线y=2x-3与x轴交点的坐标为________；与y轴交点的坐标为________；图象经过____________象限，y随x的增大而________．（1.5，0）（0，-3）一、三、四增大2、在同一直角坐标系中画出下列函数的图象，并归纳y=kx+b（k≠0）中b对函数图像的影响.（1）y=x-1，y=x，y=x+1；（2）y=-2x-1，y=-2x，y=-2x+1． 一次函数y=kx+b，y随x的增大而减小，b＞0，则它的图象经过第___________象限．一、二、四规律方法总结：b决定直线y=kx+b与y轴交点的坐标________.当b>0时，交点在原点上方.当b=0时，交点即原点.当b<0时，交点在原点下方.（0，b） 活动6小结归纳（1）一次函数y=kx+b（k≠0）的图象是什么形状？怎样用简便方法画出一个一次函数的图象？（2）一次函数有哪些性质？一次函数与正比例函数有什么关系？（3）我们是怎样对一次函数的性质进行研究的？ y=kx+b（k≠0）y=kx（k≠0）图象平移k＞0时，y随x的增大而增大；k＜0时，y随x的增大而减小．两点法画一次函数图象归纳总结：性质性质（,0）（0，b） 作业：教科书第99～100页习题19.2必做：第5，9,10题选做：第12，14题．课后作业 y=kx+b草图直线经过的象限性质K﹥0b=0b﹥0b﹤0K﹤0b=0b﹥0b﹤0完成表格 Thankyou!谢谢同学们的努力！