八年级下数学课件八年级下册数学课件《线段的垂直平分线》 北师大版 (3)_北师大版 9页

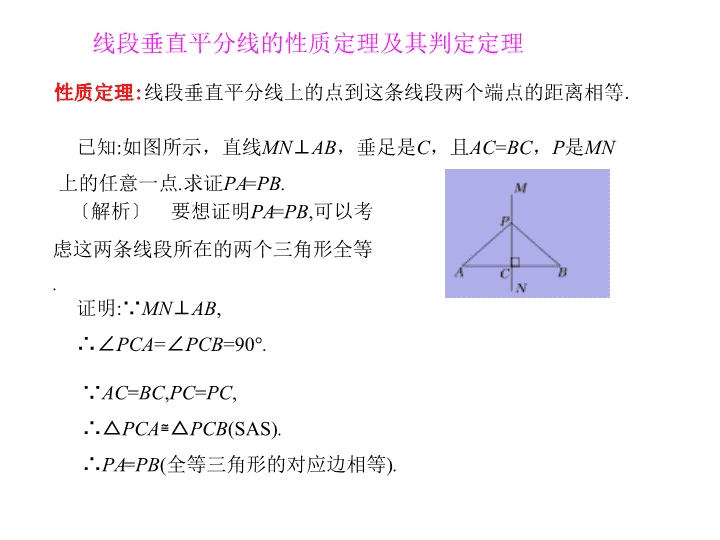
八年级数学·下新课标[北师]第一章三角形的证明3线段的垂直平分线（第1课时） 学习新知问题思考如图所示,A，B表示两个仓库,要在A，B一侧的河岸边建造一个码头,使它到两个仓库的距离相等,码头应建在什么位置?分析：线段是一个轴对称图形,其中线段的垂直平分线就是它的对称轴.我们曾经用折纸的方法,得到线段的垂直平分线上的点到这条线段两个端点的距离相等.所以在这个问题中,要在“A，B一侧的河岸边建造一个码头,使它到两个仓库的距离相等”,利用此性质就能完成. 线段垂直平分线的性质定理及其判定定理性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.已知:如图所示，直线MN⊥AB，垂足是C，且AC=BC，P是MN上的任意一点.求证PA=PB.〔解析〕要想证明PA=PB,可以考虑这两条线段所在的两个三角形全等.证明:∵MN⊥AB,∴∠PCA=∠PCB=90°.∵AC=BC,PC=PC,∴△PCA≌△PCB(SAS).∴PA=PB(全等三角形的对应边相等). 已知:线段AB，点P是平面内一点且PA=PB.求证:点P在线段AB的垂直平分线上.证法1:如图所示,过点P作已知线段AB的垂线交AB于点C.∵PA=PB,PC=PC,∴Rt△PAC≌Rt△PBC(HL).∴AC=BC,∴点P在线段AB的垂直平分线上.证法2:如图所示,取线段AB的中点C,连接PC.∵AP=BP,PC=PC,AC=CB,∴△APC≌△BPC(SSS).∴∠PCA=∠PCB(全等三角形的对应角相等).∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=∠90°,即PC⊥AB.∴点P在线段AB的垂直平分线上. 证法3:如图所示,作∠APB的平分线,交AB于点C.∵AP=BP,∠1=∠2,PC=PC,∴△APC≌△BPC(SAS).∴AC=BC,∠PCA=∠PCB(全等三角形的对应边相等,对应角相等).∵∠PCA+∠PCB=180°,∴∠PCA=∠PCB=90°.∴点P在线段AB的垂直平分线上.线段垂直平分线的判定定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上. (教材例1)已知:如图所示,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.求证:直线AO垂直平分线段BC.证明:∵AB=AC,∴点A在线段BC的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).同理,点O在线段BC的垂直平分线上.∴直线AO是线段BC的垂直平分线(两点确定一条直线). 1.如图所示,已知直线MN是线段AB的垂直平分线,垂足为D,点P是MN上一点,若AB=10cm,则BD=cm;若PA=10cm,则PB=cm.解析:∵直线MN是线段AB的垂直平分线,若AB=10cm,则BD=AB=×10=5(cm),若PA=10cm,则PB=PA=10cm.5102.如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长是12cm,AC=5cm,则AB+BD+AD=cm;AB+BD+DC=cm;△ABC的周长是cm.121217检测反馈 3.如图所示,在Rt△ABC中,∠C=90°,∠B=15°,DE是AB的垂直平分线,垂足为D,交BC于E,BE=5,则AE=,∠AEC=,AC=.530°2.54.已知线段AB及一点P,若PA=PB=3cm,则点P在上.线段AB的垂直平分线5.下列各图形中,是轴对称图形的有()①等腰三角形;②等边三角形;③点;④角;⑤两个全等三角形A.1个B.2个C.3个D.4个D 6.(2015·丽水中考)如图所示,已知△ABC,∠C=90°,AC