北师大版八年级上册数学第四章测试题含答案 9页

北师大版八年级上册数学 第四章测试题含答案 一、选择题(每题 3 分，共 30 分) 1．下列表示 y 是 x 的函数的是( ) 2．下列函数中，是一次函数的是( ) A．y＝－8x B．y＝1 x C．y＝(m＋1)x＋1 D．y＝8x2＋1 3．一次函数 y＝2x＋4 的图象与 y 轴的交点坐标是( ) A．(0，－4) B．(0，4) C．(2，0) D．(－2，0) 4．若直线 y＝kx＋b 经过第二、三、四象限，则( ) A．k>0，b>0 B．k>0，b<0 C．k<0，b>0 D．k<0，b<0 5．直线 y＝－2x＋a 经过点(3，y1)和(－2，y2)，则 y1 与 y2 的大小关系是( ) A．y1＞y2 B．y1＜y2 C．y1＝y2 D．无法确定 6．对于函数 y＝－3x＋1，下列结论正确的是( ) A．它的图象必经过点(－1，3) B．它的图象经过第一、二、三象限 C．当 x>1 时，y<0 D．y 的值随 x 值的增大而增大 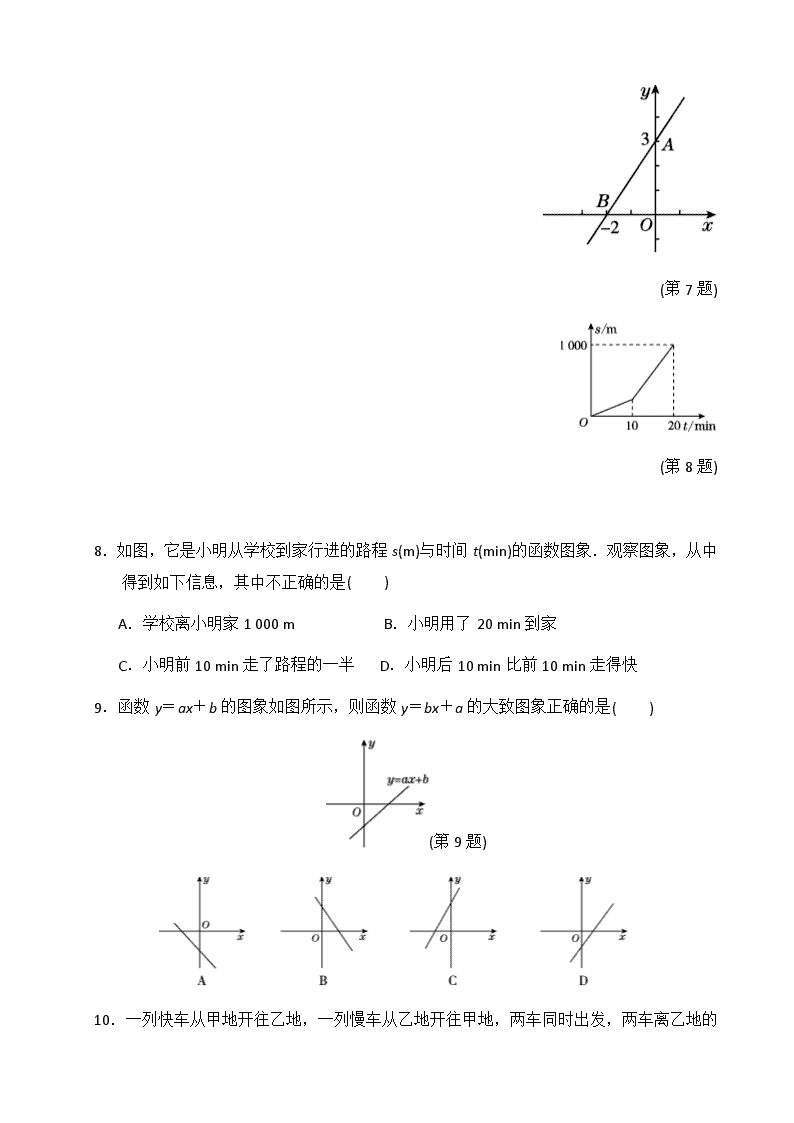7．如图，直线 y＝kx＋b 经过点 A，B，则 k 的值为( ) A．3 B.3 2 C.2 3 D．－3 2 (第 7 题) (第 8 题) 8．如图，它是小明从学校到家行进的路程 s(m)与时间 t(min)的函数图象．观察图象，从中 得到如下信息，其中不正确．．．的是( ) A．学校离小明家 1 000 m B．小明用了 20 min 到家 C．小明前 10 min 走了路程的一半 D．小明后 10 min 比前 10 min 走得快 9．函数 y＝ax＋b 的图象如图所示，则函数 y＝bx＋a 的大致图象正确的是( ) (第 9 题) 10．一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，两车离乙地的 路程 s(km)与行驶时间 t(h)的函数关系如图所示，则下列结论中错误．．的是( ) A．甲、乙两地的路程是 400 km B．慢车行驶速度为 60 km/h (第 10 题) C．相遇时快车行驶了 150 km D．快车出发后 4 h 到达乙地 二、填空题(每题 3 分，共 30 分) 11．已知 y＝(k－4)x|k|－3 是正比例函数，则 k＝________． 12．已知直线 y＝kx＋b，若 k＋b＝－5，kb＝6，那么该直线不经过第________象限． 13．若点(m，n)在函数 y＝2x＋1 的图象上，则 2m－n＝________． 14．已知点(－3，2)，(a，a＋1)在函数 y＝kx－1 的图象上，则 k＝________，a＝________. 15．直线 y＝2x＋b 与 x 轴的交点坐标是(2，0)，则关于 x 的方程 2x＋b＝0 的解是__________． 16．一次函数的图象与直线 y＝－x＋1 平行，且过点(8，2)，那么此一次函数的表达式为 ______________． 17．某公园的门票实行的收费标准是：每天进园前 20 人(含 20 人)每人 20 元，超过 20 人 时，超过部分的人数每人加收 10 元，则应收门票费用 y(元)与游览人数 x(x＞20)之间的 函数表达式为________________________________． 18．某天，某巡逻艇凌晨 1：00 出发巡逻，预计准点到达指定区域，匀速行驶一段时间后， 因中途出现故障耽搁了一段时间，故障排除后，该艇加快速度仍匀速前进，结果恰好 准点到达．如图是该巡逻艇行驶的路程 y(n mile)与所用时间 t(h)的函数图象，则该巡逻 艇原计划准点到达的时刻是__________． (第 18 题) (第 20 题) 19．直线 y＝k1x＋b1(k1＞0)与 y＝k2x＋b2(k2＜0)相交于点(－2，0)，且两直线与 y 轴围成的 三角形面积为 4，那么 b1－b2＝________． 20．已知 A 地在 B 地正南方 3 km 处，甲、乙两人同时分别从 A，B 两地向正北方向匀速直 行，他们与 A 地的距离 s(km)与所行时间 t(h)之间的函数关系的图象如图中的 OC 和 FD 所示．当他们行走 3 h 后，他们之间的距离为________km. 三、解答题(21，22 题每题 8 分，23，24 题每题 10 分，其余每题 12 分，共 60 分) 21．已知一次函数 y＝kx＋b 的图象经过 M(0，2)，N(1，3)两点． (1)求 k，b 的值； (2)若一次函数 y＝kx＋b 的图象与 x 轴的交点为 A(a，0)，求 a 的值． 22.如图，正比例函数 y＝2x 的图象与一次函数 y＝－3x＋k 的图象交于点 P(1，m)，求： (1)k 的值； (2)两条直线与 x 轴围成的三角形的面积． (第 22 题) 23．已知一次函数 y＝kx＋b 的图象经过点 A(0，2)和点 B(－a，3)，且点 B 在正比例函数 y ＝－3x 的图象上． (1)求 a 的值； (2)求一次函数的表达式，并画出它的图象； (3)若 P(m，y1)，Q(m－1，y2)是这个一次函数图象上的两点，试比较 y1 与 y2 的大小． 24．某销售公司推销一种产品，设 x(件)是推销产品的数量，y(元)是付给推销员的月报酬．公 司付给推销员的月报酬的两种方案如图所示，推销员可以任选一种与公司签订合同， 看图解答下列问题： (1)求每种付酬方案 y 关于 x 的函数表达式； (2)当选择方案一所得报酬高于选择方案二所得报酬时，求 x 的取值范围． (第 24 题) 25．如图，直线 y＝kx＋6 与 x 轴、y 轴分别交于点 E，F，点 E 的坐标为(－8，0)，点 A 的 坐标为(－6，0)，点 P(x，y)是第二象限内的直线上的一个动点． (1)求 k 的值； (2)在点 P 的运动过程中，写出△OPA 的面积 S 与 x 的函数表达式，并写出自变量 x 的取值 范围； (3)探究：当 P 运动到什么位置(求点 P 的坐标)时，△OPA 的面积为27 8 ？ (第 25 题) 26．周末，小明骑自行车从家里出发到野外郊游．他从家出发 0.5 h 后到达甲地，游玩一 段时间后按原速前往乙地．小明离家 1 h 20 min 后，妈妈驾车沿相同路线前往乙地．如 图是他们离家的路程 y(km)与小明离家时间 x(h)的函数图象．已知妈妈驾车的速度是小 明骑车速度的 3 倍． (1)求小明骑车的速度和在甲地游玩的时间． (2)小明从家出发多少小时后被妈妈追上？此时离家多远？ (3)若妈妈比小明早 10 min 到达乙地，求从家到乙地的路程． (第 26 题) 答案 一、1.D 2.A 3.B 4.D 5.B 6.C 7．B 8.C 9.B 10.C 二、11.－4 12.一 13.－1 14．－1；－1 15.x＝2 16．y＝－x＋10 17．y＝30x－200(x＞20) 18.7：00 19．4 20.1.5 三、21.解：(1)将 M，N 的坐标代入一次函数表达式，得 b＝2，k＋b＝3， 解得 k＝1. 即 k，b 的值分别是 1 和 2. (2)将 k＝1，b＝2 代入 y＝kx＋b，得 y＝x＋2. 因为点 A(a，0)在 y＝x＋2 的图象上，所以 0＝a＋2. 所以 a＝－2. 22．解：(1)因为正比例函数 y＝2x 的图象与一次函数 y＝－3x＋k 的图象交于点 P(1，m)， 所以把点 P(1，m)的坐标代入，得 m＝2，m＝－3＋k，解得 k＝5. (2)由(1)可得点 P 的坐标为(1，2)， 故所求三角形的高为 2. 由(1)可得一次函数的表达式为 y＝－3x＋5. 令 y＝0，则 0＝－3x＋5，得 x＝5 3. 所以一次函数的图象与 x 轴交点的横坐标为5 3. 所以所求三角形的面积为1 2×5 3×2＝5 3. 23．解：(1)因为点 B(－a，3)在正比例函数 y＝－3x 的图象上， 所以 3＝－3×(－a)，则 a＝1. (2)由(1)得点 B 的坐标为(－1，3)．将点 A(0，2)和点 B(－1，3)的坐标代入 y＝kx＋b，得 b ＝2，－k＋b＝3， 解得 k＝－1. 所以一次函数的表达式为 y＝－x＋2.画图象略． (3)因为－1＜0， 所以 y 随 x 的增大而减小． 又因为 m＞m－1， 所以 y1＜y2. 24．解：(1)设方案一的表达式为 y＝kx，把(40，1 600)的坐标代入表达式，可得 k＝40，故 表达式为 y＝40x； 设方案二的表达式为 y＝ax＋b，把(40，1 400)和(0，600)的坐标代入表达式，可得 a＝20， b＝600，故表达式为 y＝20x＋600. (2)根据两直线相交可得方程 40x＝20x＋600，解得 x＝30. 结合图象可得，当 x＞30 时，选择方案一所得报酬高于选择方案二所得报酬． 25．解：(1)因为点 E(－8，0)在直线 y＝kx＋6 上，所以－8k＋6＝0. 所以 k＝3 4. (2)由(1)得 y＝3 4 x＋6， 所以 S＝1 2×6× 3 4 x＋6 . 所以 S＝9 4 x＋18(－8＜x＜0)． (3)由 S＝9 4 x＋18＝27 8 得 x＝－13 2 ，则 y＝3 4× －13 2 ＋6＝9 8 ， 所以 P －13 2 ，9 8 . 即当 P 运动到点 －13 2 ，9 8 时， △ OPA 的面积为27 8 . 26．解：(1)观察图象，可知小明骑车的速度为10 0.5 ＝20(km/h)，在甲地游玩的时间是 1－0.5 ＝0.5(h)． (2)妈妈驾车的速度为 20×3＝60(km/h)． 如图，设直线 BC 对应的函数表达式为 y＝20x＋b1，把点 B(1，10)的坐标代入，得 20×1＋ b1＝10，则 b1＝－10. 所以直线 BC 对应的函数表达式为 y＝20x－10. (第 26 题) 设直线 DE 对应的函数表达式为 y＝60x＋b2，把点 D 4 3 ，0 的坐标代入，得 60×4 3 ＋b2＝0， 则 b2＝－80. 所以直线 DE 对应的函数表达式为 y＝60x－80. 当小明被妈妈追上时，两人走过的路程相等，则 20x－10＝60x－80， 解得 x＝1.75， 20×(1.75－1)＋10＝25(km)． 所以小明从家出发 1.75 h 后被妈妈追上，此时离家 25 km. (3)设从妈妈追上小明的地点到乙地的路程为 z km. 根据题意，得 z 20 － z 60 ＝10 60 ，解得 z＝5. 所以从家到乙地的路程为 5＋25＝30(km)．