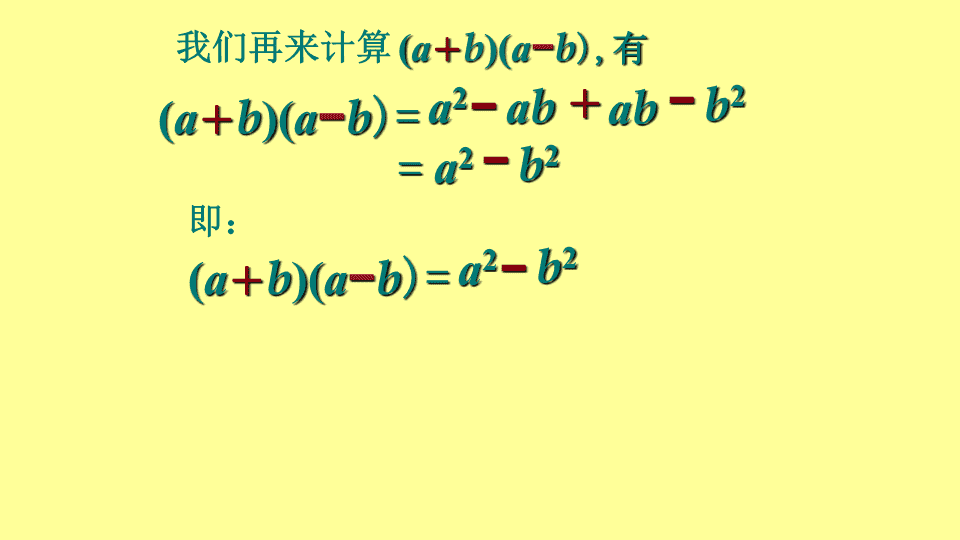八年级上数学课件- 14-2-1 平方差公式 课件（共22张PPT）_人教新课标 22页

14.2.1平方差公式 (a+b)(a-b)=? 计算下列多项式的积，你能发现什么规律？ (1) (x+1)(x-1）= (2) (m+2)(m-2）= (3) (2x+1)(2x-1）= x2 -x +x -1 m2-2m+2m-4 (2x)2 -2x+2x -1 x2= = -1 m2 -4 = 4x2 -1 我们再来计算 即： 平方差公式 (a+b)(a-b)=(a)2-(b)2 相同为a 相反为b 合理加括号 平方差公式 运用公式的窍门： 相反项）（相同项相反项相同项  )( 2. 再写成两项和乘以两项差的形式； 3.然后可以运用公式写出，即用 相同项的平方减去相反项的平方。 22)( （相反项）相同项  判断下列式子是否可用平方差公式。 (1)(-a+b)(a+b) (2) (-a+b)(a-b) (3)(a+b)(a-c) (4)(2+a)(a-2) （5） (1-x)(-x-1) （6）(-4k3+3y2)(-4k3-3y2) 是 否 是 是 是 否 例1 运用平方差公式计算： 分析：在（1）中，可以把3x看成a,2看成b,即 (3x)2 22 解： 22 (3x)2 9x2= 4 例1 运用平方差公式计算： 分析：在（2）中，可以把（ ）看成a, （　）看成b 解： b2 (2a)2 4a2 = = b2 2a b 例1 运用平方差公式计算： 分析：在（3）中，可以把（ ）看成a, （　）看成b 解： (2y)2 x2= 4y2 2y 你还有其它的计 算方法吗？ ⑴ (a+1)(a-1)= ⑵ (3+x)(3-x)= ⑶ (a+2b)(a-2b)= ⑷ (3x+5y)(3x-5y)= ⑸ (10s-3t)(10s+3t)= a2-1 9-x2 a2-(2b)2 =a2-4b2 (3x)2-(5y)2 =9x2-25y2 (10s)2-(3t)2 =100s2-9t2 （6）(−3x+2)(−3x−2) =9x2－4 （8）(−3x+y)(3x+y) （7）(−4a+3)(−4a−3) （9）(y−x)(−x−y) =16a2－9 =9x2－y2 =x2－y2 (10)(-m+n)(-m-n)= (-m)2-n2 =m2-n2 例2：计算 （1）102×98 (2) (y+2)(y-2)-(y-1)(y+5) （1）解：原式=(100+2)(100-2) =1002-22 =10000-4 =9996 例2：计算 （1）102×98 (2) (y+2)(y-2)-(y-1)(y+5) (2)解：原式=y2-4-(y2+4y-5) =y2-4-y2-4y+5 =-4y+1 运用平方差公式计算：P108 (1) (a+3b)(a-3b） (2) (3+2a)(-3+2a） (3) (3x+4) (3x-4) – (2x+3) (3x-2) 解： (1) (a+3b)(a-3b）= (3b)2a2 a2= 9b2 (2) (3+2a)(-3+2a）= 32 (2a)2 4a2= (2a+3)(2a-3） = 9 (3) (3x+4)(3x-4)- (2x+3)(3x-2) = 9x2- 42 -(6x2+5x-6) = 9x2-16-6x2-5x+6 = 3x2-5x-10 （4）1992×2008 （1）1992×2008 =(2000 −8) ×(2000+8 ) =20002 −82 =4000 000−64 =3 999 936 解： （5）996×1004 （2）996×1004 =(1000 −4) ×(1000+4 ) =10002 −42 =1000 000−16 =999 984 (1) (x+3)( )=x2-9 (2) (-1-2x)( 2x-1)= (3) (m+n)( )=n2-m2 (4) ( )(-y-1)=1-y2 (5) (-3a2+2b2)( )=9a4-4b4 X-3 1-4x2 n-m -1+y -3a2-2b2 （1）(x+y)(x-y)(x2+y2) 解：原式 =(x2-y2)(x2＋y2) =x4-y4 （2） (x-y)(x+y)(x2+y2)(x4+y4)(x8+y8) 解：原式= (x2－y2)(x2+y2)(x4+y4)(x8+y8) =(x4－y4) (x4+y4)(x8+y8) =(x8－y8 )(x8+y8) =x16－y16 （3） (3a＋b＋c)(3a＋b－c) 解：原式=[(3a＋b) ＋c][(3a＋b) －c] =(3a＋b)2－c2 =9a2＋6ab＋b2－c2 我学会了平方差公式，知道 了平方差公式的特点 我学会了用几何方法验证平方差 公式，让我体会到了数形结合的 数学思想 我还找到了一些运用 平方公式的小窍门 这节课你有哪些收获？ a b ba - ba - ba + b 如左下图,边长为a的大正方形中有一个边 长为b的小正方形. (1)图中阴影部分的面积为________.22 - ba (2)将阴影部分拼成右图的一个长方形,这个长 方形的长是____,宽是____,面积是_________.ba + ba - )ba)(ba( -+ (3)比较(1)(2)的结果即可得到______________.(a+b)(a-b)=a2-b2 有趣的数学