八年级上数学课件《一次函数与二元一次方程》 (11)_苏科版 23页

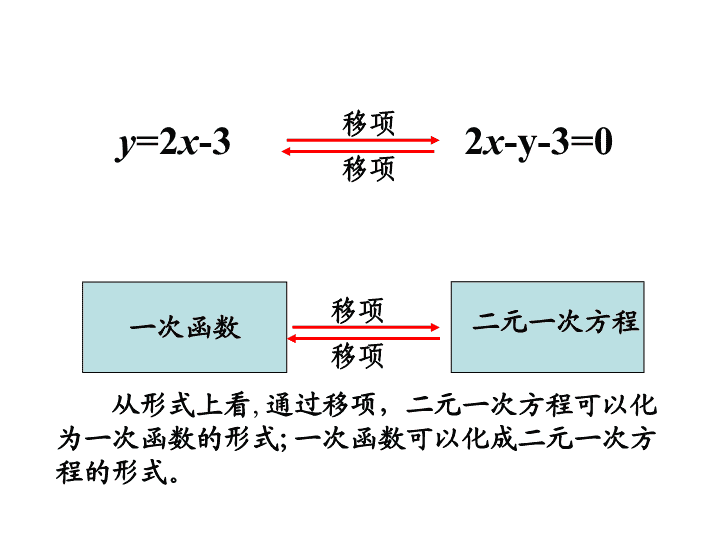
二元一次方程 2x-y-3=0y=2x-3 移项 移项 一次函数 从形式上看,通过移项，二元一次方程可以化 为一次函数的形式;一次函数可以化成二元一次方 程的形式。 移项 移项 6.5 一次函数与二元一次方程 二元一次方程2x-y-3=0的解与 一次函数y=2x-3图像上点有什么关系？ 1 活动一 1．在坐标系中画出一次函数y＝ 2x－3的图像. 2．在（1）中所得的图像上任取一点,它的坐标 是二元一次方程2x-y-3=0的解吗?为什么？ 活动一 3．二元一次方程2x－y－3＝0有多少个解？ 请说出其中的几个． 4．在（1）中的直角坐标系中描出这些以方程 2x－y－3＝0的解为坐标的点，你有什么发现？ x y 0 y = 2x-3  5,1   3,0   1,1   1,2  3,3  0,2 3 二元一次方程2x-y-3=0 的解与一次函数y=2x-3图 像上的点有什么关系？ 二元一次方程 一次函数 以二元一次方程的一个 解为坐标就是相应函数 图像上的点 一次函数的图像上 任一点坐标都是相 应方程的一个解 结论1： 一般地，一次函数图像上任意一点的坐标 都是二元一次方程的一个解；以二元一次方程 的解 为坐标的点都在一次函数的图像上． 1．若方程x－y＝1有一个解为 则一次函数y＝x－1的图像上必有点 .    x＝2， y＝1． 2．若一次函数y＝2x－4的图像上有一点的坐标是（3，2）． 则方程2x－y－4＝0必有一个解为 . 尝试练习： 1.在刚才平面直角坐标系中再画出方程 x+y-3=0所对应的直线. 2 2x-y=1 这 两个图像有交点吗？ 2.解方程组 2 3 0 3 0 x y x y        结论：两图像的交点(2,1),也是方程组的解。 两个图像的交点坐标与方程组的解有什么关系？ 交点坐标是多少？ 结论2：一般的，如果2个一次函数的图像 有一个交点，那么交点的坐标就是相应的 二元一次方程组的解. 归纳总结: 从数的角度看： 求二元一次方程组的解 x为何值时，两个函数的值相等 从形的角度看： 求二元一次方程组的解 是确定两条直线交点的坐标 ∵ 它们的交点坐标为P（2，1） X=2 ∴原二元一次方程组的解是 y=1 解：由x+2y=4，得 1 22y x   由2x-y=3,得 y=2x-3 在同一直角坐标系中，画 出这两个函数的图像. x y O P（2，1） 32  xy 22 1  xy 利用一次函数的图像解二元一次方程组 x+2y=4 2x-y=3 用一次函数的图象解二元一次方程组的方法 称为二元一次方程组的图像解法 ⑴把二元一次方程组中的方程化成 一次函数的形式; ⑵在直角坐标系中画出两个一次函数 的图像; ⑶找出直线交点的坐标; ⑷写出方程组的解。 简称为：变函数 画图像 找交点 写结论 一般步骤： 8 6 4 2 -2 -4 -6 -8 -10 -5 5 10 y o x x-y=0 2x+y=5 作出图象： 观察图象得：交点(1.7,1.7) ∴方程组的解为 x=1.7 y=1.7精确！ 图象法： 用图像法解方程组 代数法： x=5/3 y=5/3 ∴方程组的解为 用作图象的方法可以直观地获得问题的 结果,但有时却难以准确.为了获得准确 的结果,我们一般用代数方法. 近似！ 练习： 思考：用图象法解方程组有何优点和不足？ 优点：形象直观 缺点：是近似值，不够准确 1.因为方程组 的解是 所以一次函数y =－x＋4与y=2x＋1的图象交点坐标 为 ．      12 4 yx yx 1 3 x y    （1，3） 尝试练习： P(1,1) y=-x+2 3 1 2 2y x  2.如图，根据图像写出方程组      0123 02 yx yx 的解 。     1 1 y x 变式：已知三条直线y=2x-3,y= -2x+1和 y=kx-2相交于同一点，求交点坐标和k的 值。 3.已知直线y=kx+5和y=-2x-b的图象的交点是 (-1,3),则k=______ , b=________ 思考： 一次函数y=–x+1，y=–x+2的图象之间有何关系？ 1 2 y x y x       那么方程组 解是_______. u通过以上学习你能发现二元一次方 程组的解有几种情况？ 二元一次方程组的解有以下三种情况 ①只有一组解（两直线只有一个交点） ②有无穷多组解（两直线直线重合） ③无解（两直线平行） 试判断下列方程组是否有解 看谁快 （1）通过本节课学习，你学会了哪些知识？ （2）掌握了哪些数学思想？