数学教案函数教案2 4页

‎ ‎ ‎6.1函数 教学目标：‎ ‎【知识目标】1、初步掌握函数概念，能判断两个变量间的关系是否可看作函数。‎ ‎2、根据两个变量间的关系式，给定其中一个量，相应地会求出另一个量的值。‎ ‎3、会对一个具体实例进行概括抽象成为数学问题。‎ ‎【能力目标】1、通过函数概念，初步形成学生利用函数的观点认识现实世界的意识和能力。‎ ‎2、经历具体实例的抽象概括过程，进一步发展学生的抽象思维能力。‎ ‎【情感目标】1、经历函数概念的抽象概括过程，体会函数的模型思想。‎ ‎2、让学生主动地从事观察、操作、交流、归纳等探索活动，形成自己对数学知识的理解和有效的学习模式。‎ 教学重点：‎ 1、 掌握函数概念。‎ 2、 判断两个变量之间的关系是否可看作函数。‎ 3、 能把实际问题抽象概括为函数问题。‎ 教学难点：‎ 1、 理解函数的概念。‎ 2、 能把实际问题抽象概括为函数问题。‎ 教学过程设计：‎ ‎ 一、创设问题情境，导入新课 ‎ 『师』：同学们，你们看下图上面那个像车轮状的物体是什么？‎ ‎ 『生』：摩天轮。‎ ‎ 『师』：你们坐过吗？‎ 4‎ ‎ ‎ ‎ ……‎ ‎ 『师』：当你坐在摩天轮上时，人的高度随时在变化，那么变化是否有规律呢？‎ ‎ 『生』：应该有规律。因为人随轮一直做圆周运动。所以人的高度过一段时间就会重复依次，即转动一圈高度就重复一次。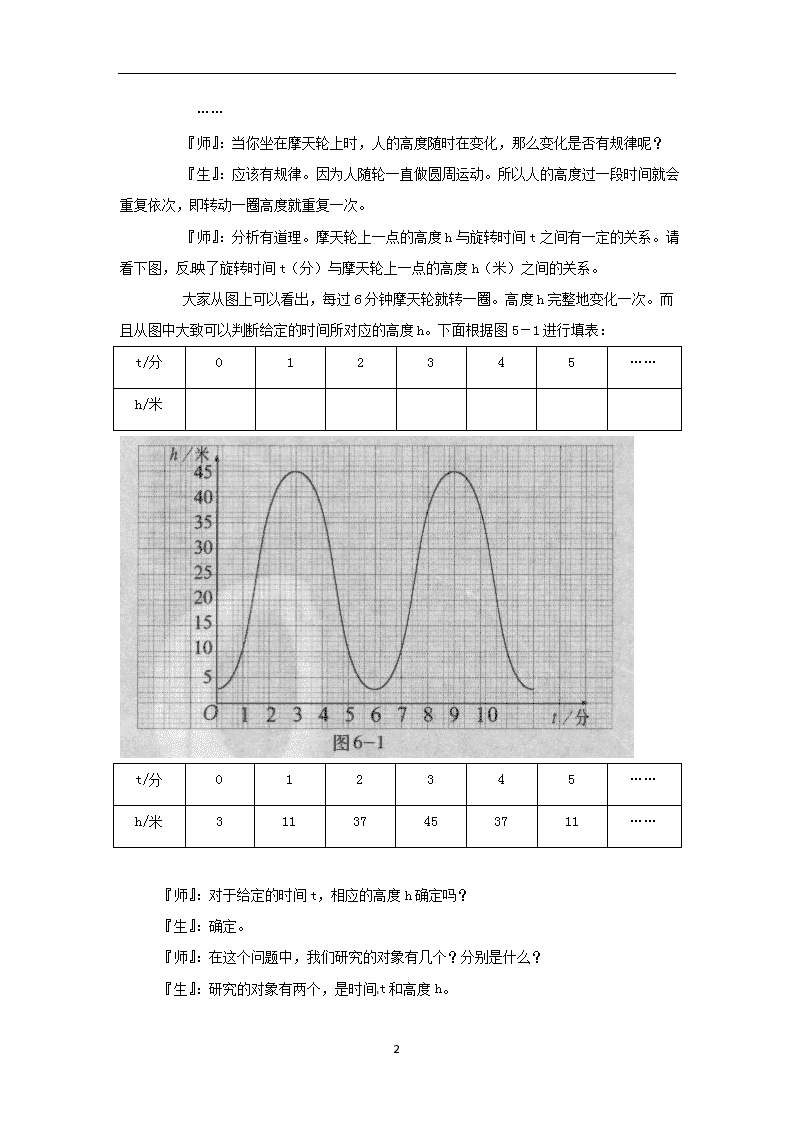‎ ‎ 『师』：分析有道理。摩天轮上一点的高度h与旋转时间t之间有一定的关系。请看下图，反映了旋转时间t（分）与摩天轮上一点的高度h（米）之间的关系。‎ ‎ 大家从图上可以看出，每过6分钟摩天轮就转一圈。高度h完整地变化一次。而且从图中大致可以判断给定的时间所对应的高度h。下面根据图5－1进行填表：‎ t/分 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎……‎ h/米 t/分 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎……‎ h/米 ‎3‎ ‎11‎ ‎37‎ ‎45‎ ‎37‎ ‎11‎ ‎……‎ ‎『师』：对于给定的时间t，相应的高度h确定吗？‎ ‎『生』：确定。‎ ‎『师』：在这个问题中，我们研究的对象有几个？分别是什么？‎ ‎『生』：研究的对象有两个，是时间t和高度h。‎ 4‎ ‎ ‎ ‎『师』：生活中充满着许许多多变化的量，你了解这些变量之间的关系吗？如：弹簧的长度与所挂物体的质量，路程的距离与所用时间……了解这些关系，可以帮助我们更好地认识世界。下面我们就去研究一些有关变量的问题。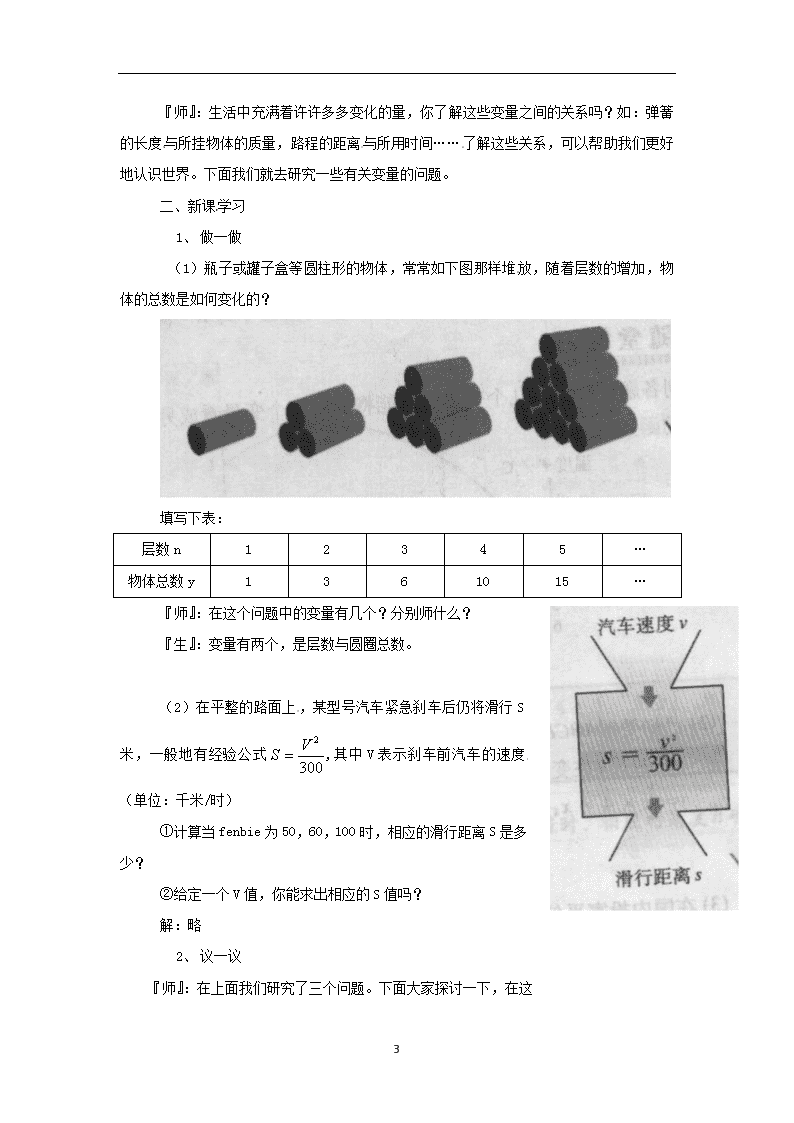‎ 二、新课学习 1、 做一做 ‎（1）瓶子或罐子盒等圆柱形的物体，常常如下图那样堆放，随着层数的增加，物体的总数是如何变化的？‎ 填写下表：‎ 层数n ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎…‎ 物体总数y ‎1‎ ‎3‎ ‎6‎ ‎10‎ ‎15‎ ‎…‎ ‎『师』：在这个问题中的变量有几个？分别师什么？‎ ‎『生』：变量有两个，是层数与圆圈总数。‎ ‎（2）在平整的路面上，某型号汽车紧急刹车后仍将滑行S米，一般地有经验公式,其中V表示刹车前汽车的速度（单位：千米/时）‎ ‎①计算当fenbie为50，60，100时，相应的滑行距离S是多少？‎ ‎②给定一个V值，你能求出相应的S值吗？‎ 解：略 2、 议一议 4‎ ‎ ‎ ‎『师』：在上面我们研究了三个问题。下面大家探讨一下，在这三个问题中的共同点是什么？不同点又是什么？‎ ‎『生』：相同点是：这三个问题中都研究了两个变量。‎ 不同点是：在第一个问题中，是以图象的形式表示两个变量之间的关系；第二个问题中是以表格的形式表示两个变量间的关系；第三个问题是以关系式来表示两个变量间的关系的。‎ ‎『师』：通过对这三个问题的研究，明确“给定其中某一个变量的值，相应地就确定了另一个变量的值”这一共性。‎ 1、 函数的概念 在上面各例中，都有两个变量，给定其中某一各变量（自变量）的值，相应地就确定另一个变量（因变量）的值。‎ 一般地，在某个变化过程中，有两个变量x和y，如果给定一个x值，相应地就确定了一个y值，那么我们称y是x的函数，其中x是自变量，y是因变量。‎ 三、随堂练习 ‎ 书P179 随堂练习1、2、3‎ 四、本课小结 1、 初步掌握函数的概念，能判断两个变量间的关系是否可看作函数。‎ 2、 在一个函数关系式中，能识别自变量与因变量，给定自变量的值，相应地会求出函数的值。‎ 3、 函数的三种表达式：‎ （1） 图象；（2）表格；（3）关系式。‎ 五、探究活动 ‎ 为了加强公民的节水意识，某市制定了如下用水收费标准：每户每月的用水不超过10吨时，水价为每吨1.2元；超过10吨时，超过的部分按每吨1.8元收费，该市某户居民5月份用水x吨（x >10），应交水费y元，请用方程的知识来求有关x和y的关系式，并判断其中一个变量是否为另一个变量的函数？‎ ‎（参考答案：Y=1.8x-6或）‎ 六、课后作业 4‎