苏教版数学八年级上册教案6-3一次函数的图像（1） 3页

- 1 - 6.3 一次函数的图像（1） 教学目标 【知识与能力】 通过生活中的实例感受一次函数的图像，知道一次函数的图像是一条直线． 【过程与方法】 经历一次函数图像的作图过程，初步了解作函数图像的一般步骤，并会选取适当的两个点画 一次函数的图像 【情感态度价值观】 通过画函数图像，提高画图技能，观察、比较、抽象与概括的能力，以及用“数形结合”的 思想方法解决数学问题的能力 教学重难点 【教学重点】 能熟练的做出一次函数的图像；归纳作函数图像的一般步骤；理解一次函数的函数表达式与 图像的对应关系 【教学难点】 理解一次函数的代数表达式与图像的对应关系 课前准备 无 教学过程 一、复习 1.回忆： 叫做这个函数的图象。 那么一次函数的图象是怎样的？（导入新课） 2.点燃一支香，感受它的长度随着时间的变化而变化 若每 5 分钟燃烧 4cm，填写下表 点燃时间/min 0 5 10 15 20 香的长度/cm 设香的长度为 y(cm)，燃烧时间 x(min)，你能写出 y 与 x 之间的函数关系式吗？ 以 x 轴表示香的燃烧时间，以 y 轴表示香的长度，建立直角坐标系，并分别描出上表提供的 点，5 个点在一条直线上吗？ 二、创设情境 点燃一支香，感受它的长度随时间的变化而变化． 观察上面的图片，说一说获得哪些信息？ 要求：通过生活中的情景引入新课，提高学生的学习兴趣． 探究活动 1 1．将你的观察结果填在书中的表格内． 2．如果用 y （cm）表示香的长度、x（min）表示香燃烧的时间，你能写出 y 与 x 之间的函 数表达式吗？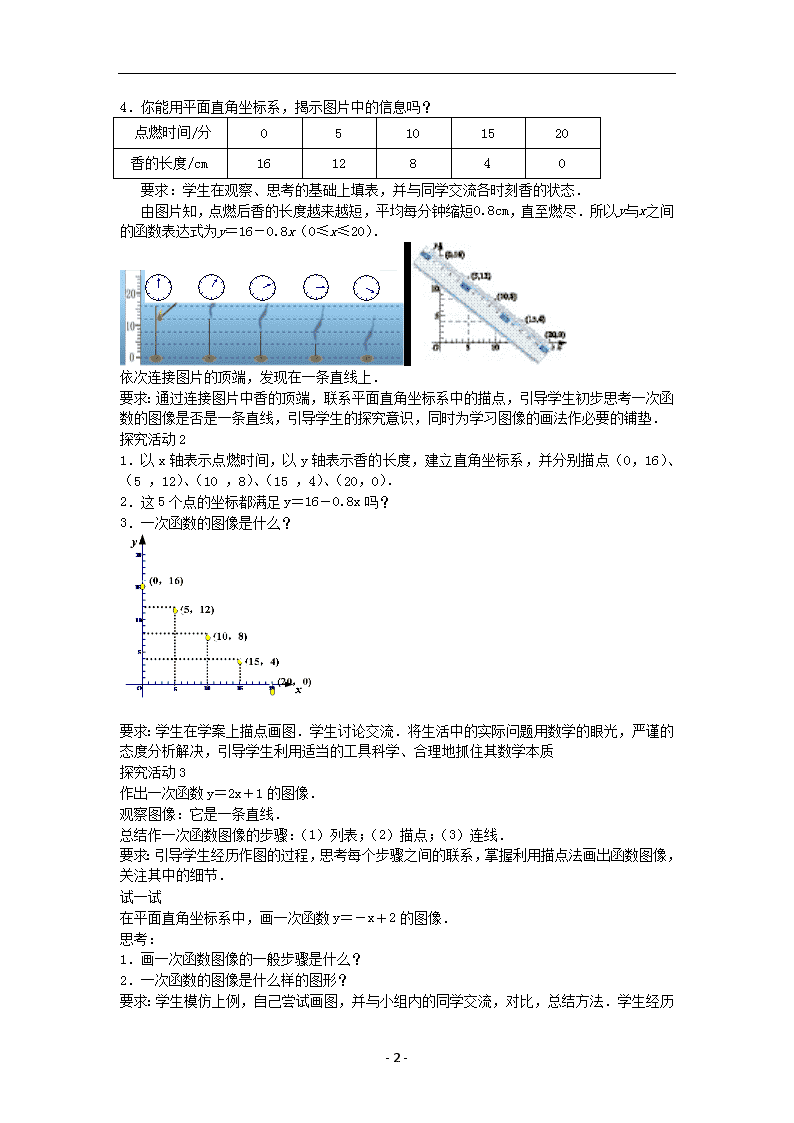 3．依次连接图片中香的顶端，你有什么发现？ - 2 - 4．你能用平面直角坐标系，揭示图片中的信息吗？ 点燃时间/分 0 5 10 15 20 香的长度/cm 16 12 8 4 0 要求：学生在观察、思考的基础上填表，并与同学交流各时刻香的状态． 由图片知，点燃后香的长度越来越短，平均每分钟缩短0.8cm，直至燃尽．所以y与x之间 的函数表达式为y＝16－0.8x（0≤x≤20）． 依次连接图片的顶端，发现在一条直线上． 要求：通过连接图片中香的顶端，联系平面直角坐标系中的描点，引导学生初步思考一次函 数的图像是否是一条直线，引导学生的探究意识，同时为学习图像的画法作必要的铺垫． 探究活动 2 1．以 x 轴表示点燃时间，以 y 轴表示香的长度，建立直角坐标系，并分别描点（0，16）、 （5 ，12）、（10 ，8）、（15 ，4）、（20，0）． 2．这 5 个点的坐标都满足 y＝16－0.8x 吗？ 3．一次函数的图像是什么？ 要求：学生在学案上描点画图．学生讨论交流．将生活中的实际问题用数学的眼光，严谨的 态度分析解决，引导学生利用适当的工具科学、合理地抓住其数学本质 探究活动 3 作出一次函数 y＝2x＋1 的图像． 观察图像：它是一条直线． 总结作一次函数图像的步骤：（1）列表；（2）描点；（3）连线． 要求：引导学生经历作图的过程，思考每个步骤之间的联系，掌握利用描点法画出函数图像， 关注其中的细节． 试一试 在平面直角坐标系中，画一次函数 y＝－x＋2 的图像． 思考： 1．画一次函数图像的一般步骤是什么？ 2．一次函数的图像是什么样的图形？ 要求：学生模仿上例，自己尝试画图，并与小组内的同学交流，对比，总结方法．学生经历 - 3 - 画图的过程，感受画图的方法． 想一想 1．画一次函数图像的一般步骤； 2．画一次函数的图像有没有简捷的方法呢？ 3．通常选取哪两点比较方便？ 要求：学生结合自己的观察和动手实践的经验回答．根据基本事实，“两点确定一条直线”， 画一次函数图像时，只要先确定这个图像上两个点的位置，再过这两点画直线就可以了．在 巩固画图过程的基础上，引导学生思考如何简化作图的过程，培养学生勤学好思的良好习惯． 三、例题分析 例 在直角坐标系中，画一次函数 y＝－3x＋3 的图像． 试判断：在点 A（2，5）、 B（－1，6）、C（3，12）、D（－2，3）、E（5，－12）中，哪些 点在此函数的图像上？ 要求：学生利用总结的方法，画图实践．通过带入函数表达式结合观察图像做出判断．巩固 画一次函数图像的技能．体会“数形结合”的思想方法． 四、课堂练习 1．下列两点在函数 y＝－2x＋3 图像上的是 （ ）． A．原点和点（1，1）； B．点（1，1）和点（2，3）； C．点（0，3）和点（1，1）； D．点（0，3）和点（2，3）．． 要求：学生解答，互相交流方法． 2．在同一坐标系中，画一次函数 y＝2x＋2、y＝2x－1、y＝2x－2 的图像． 观察这 3 个函数的图像，你有什么发现？ 要求：学生选取合适的点，做出函数图像．观察可得：彼此互相平行． 3．画出函数 y＝－3x＋2 的图像，并指出图像所经过的象限； ①试判断点 P（2，5）是否在此函数的图像上，并说明理由． ②求出此直线与坐标轴交点的坐标； ③求此直线与坐标轴所围成的三角形面积． 要求：学生分组合作，交流完成．通过画函数图像，提高画图技能，观察、比较、抽象与概 括的能力，以及用“数形结合”的思想方法解决数学问题的能力． 五、小结思考 请同学说一说自己在本节课中的收获和困惑． 1．作一次函数的步骤． 2．明确一次函数的图像是一条直线，因此在作图时，只要确定两点就可以了．