八年级上数学课件《轴对称的性质》 (13)_苏科版 23页

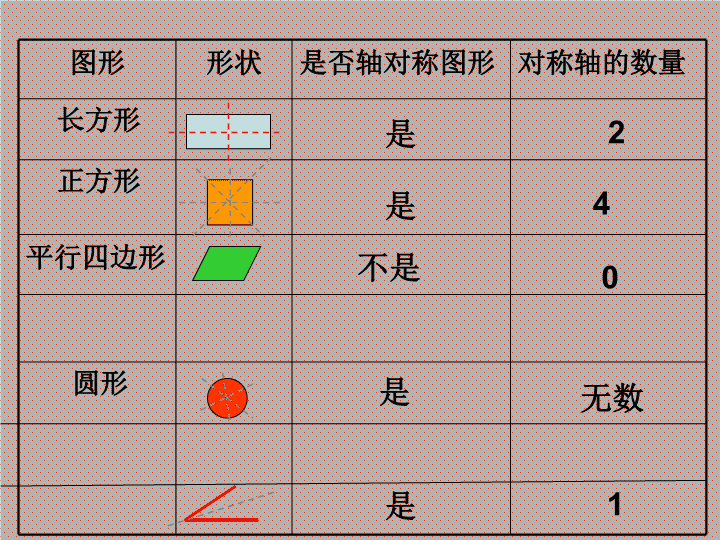
数学 八年级上 苏科版 根据“轴对称的”的定义： 如果两个图形成轴对称，那么这两 个图形全等，即成轴对称的两个图形 全等　 温故知新 图形 形状 是否轴对称图形 对称轴的数量 长方形 正方形 平行四边形 圆形 是 是 是 不是 2 4 无数 0 是 1 学习目标： 1、知道线段垂直平分线的概念 2、知道成轴对称的两个图形全等 3、成轴对称的两个图形中，对应点 的连线被对称轴垂直平分　 情境导入： 同学们记录的图形照镜子，你有什么评价？ （3） （4） （1） （2） 2.2　轴对称的性质(1) A 如图所示，把一张纸折叠后，用针扎一个孔； 再把纸展开，两针孔分别记为点A、点A′，折 痕记为l ；连接AA′，AA′与l相交于点O ． 你有什么发现 （小组交流）？ ● l l 活动一： ● A′O ● 2.2　轴对称的性质(1) 所以 线段OA、OA′重合， 因为 ∠1＝∠2 且 ∠1＋∠2＝180°， 即 O是AA′的中点． 所以 ∠1＝∠2＝90°． l A A′● ● 2 o 1 所以 l 垂直且平分AA′． 因为 把纸沿折痕 l 折叠时，点A、A′重合， 2.2　轴对称的性质(1) 垂直并且平分一条线段的直线，叫做这条线段的垂 直平分线(midpoint perpendicular). l 　　如图，直线 l 交线段AB于点O, ∠1＝90°，AO＝BO， 直线l是线段AB的垂直平分线． BA ● ● 1 O 2.2　轴对称的性质(1) 仿照上面的操作，在对折后的纸上再扎一个孔，把纸展 开后记这两个针孔为点B、点B′，连接AB、A′B′、BB′．你 有什么新的发现？ A′ B′ l 活动二： 2.2　轴对称的性质(1) 如图，并仿照上面进行操作，扎孔、展开、标记、连线． △ABC 与△A′B′C′有什么关系？ 你能得出什么结论？ A C B A′ B′ ●C′ l 活动三： 2.2　轴对称的性质(1) 1．成轴对称的两个图形全等． 2．成轴对称的两个图形中，对应点的连线被对 称轴垂直平分． 轴对称的性质： B 'B A ' C C ' B 'B A ' 说一说 轴对称的性质 A A 2.2　轴对称的性质(1) 思考： 我们如何确定对称图形的对称轴？ 小组讨论交流 ● ● ● ● A DC B ● ● ● ● F E H G l 例1　小明取一张纸，用小针在纸上扎出“4”，然后将纸 放在镜子前． (1)图中两个“4”有什么关系？ （2）你能画出镜子所在直线l的位置吗？ 方法（1）2 2.2　轴对称的性质(1) ● ● ● ● A DC B ● ● ● ● F E H G l （3）图中点A、B、C、D的对称点分别 是 ，线段AC、AB的对应线段 分别是 ，CD= ， ∠CAB= ，∠ACD= . E、G、F、H EF、EG FH ∠FEG ∠EFH 2.2　轴对称的性质(1) （4）连接AE、BG， AE与BG平行吗？为什么？ 因为 A和E，B和G是关于直线 l 的对称点， ● ● ● ● A DC B ● ● ● ● F E H G l 所以 l⊥AE ，l⊥BG． 所以 AE ∥BG． 解：（3）平行． 2.2　轴对称的性质(1) （5） AE与BG平行，能说明轴对称图形对称点的连线一 定互相平行吗？ 解：（4） 不一定． ● ● ● ● A DC B ● ● ● ● F E H G l 如图，对称点的连线DH、CF就不互相平行，而是 在同一条直线上， 从而说明轴对称图形对称点的连线 互相平行或在同一条直线上． 2.2　轴对称的性质(1) ● ● ● ● A DC B ● ● ● ● F E H G l （6）延长线段CA、FE，连接CB、FG并延长，作直线AB、 EG，你有什么发现吗？ 　　轴对称图形中的对称线段所在直线的交点在对称轴上 或对称线段所在直线互相平行． 2.2　轴对称的性质(1) 对称轴 AB=CD，BE=CE ∠B=∠C 1. 如果两个图形关于某条直线对称，那 么对应点所连的线段被 垂直平分。 2. 下图是轴对称图形，相等的线段 是 ，相等的角 。 A B C DE 实战演练 3．两个图形关于某直线对称，对称点一定 ( ) A．这直线的两旁 B．这直线的同旁 C．这直线上 D．这直线两旁或这直线上 D 4．轴对称图形沿对称轴对折后，对称轴两旁的 部分（ ） A．完全重合 B．不完全重合 C．两者都有 A 实战演练 5. 如图，△ABC与△DEF关于直线L成轴对称。 ①请写出其中相等的线段； ②如果△ABC的面积为6cm,且DE=3cm， 求△ABC中AB边上的高h。 L C A B E F D 实战演练 回顾与思考： 　　通过本节课的学习，你有什么收获？ 还有哪些疑惑？ 2.2　轴对称的性质(1) 小结 （1）成轴对称的两个图形全等． 　　（2）如果两个图形成轴对称，那么对称轴是对称 点连线的垂直平分线． 1．轴对称的性质： 2．轴对称图形对称点的连线互相平行或在同一条 直线上． 3．轴对称图形中的对称线段所在直线的交点在对称 轴上或对称线段所在直线互相平行． 2.2　轴对称的性质(1)