2020-2021八年级数学上册一次函数单元测试卷（新人教版pdf格式） 14页

2020-2021 学年新初二数学上册单元测试卷 一次函数 第Ⅰ卷（选择题 共 30 分） 一、选择题：本题共 10 个小题，每小题 3 分，共 30 分。在每小题给出的四个选项中，只有一项是 符合题目要求的。 1．(本题 3 分)下列函数：①y＝ 6 x ；②y＝－ 4 x ；③y＝3－ 1 2 x；④y＝3x2－2．其中是一次函数的 有（ ） A．4 个 B．3 个 C．2 个 D．1 个 【答案】C 【解析】 解：由题可得，是一次函数的有：①y＝ ；③y＝3－ x， ∴一次函数有 2 个， 2．(本题 3 分)一个正比例函数的图象经过点 ( 2 ,4 ) ，它的表达式为 （ ） A． 2yx B． 2yx C． 1 2yx D． 1 2yx 【答案】A 【解析】 解：设正比例函数解析式为 (0)ykx k,因为函数的图象经过点 ， 所以 42,2 kk   ， 所以解析式为 故选 A． 3．(本题 3 分)函数 y=3x-5 的图象不经过（ ） A．第一象 B．第二象限 C．第三象限 D．第四象限 【答案】B 【解析】 解：∵k=3＞0， ∴图象经过一、三象限， ∵b=-5＜0， ∴图象经过第三、四象限， 故图象不经过第二象限． 故选：B． 4．(本题 3 分)如果直线 y＝kx+b 经过一、二、四象限，则有（ ） A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＜0，b＜0 【答案】C 【解析】 解：由一次函数 y＝kx+b 的图象经过第一、二、四象限， 又由 k＜0 时，直线必经过二、四象限，故知 k＜0． 再由图象过一、二象限，即直线与 y 轴正半轴相交，所以 b＞0． 故选：C． 5．(本题 3 分)函数 23yx中自变量 x 是取值范围是（ ） A． 3 2x  B． 3 2x  C． 3 2x  D． 3 2x  【答案】B 【解析】 由二次根式的被开方数的非负性得： 2 3 0x  解得 3 2x  故选：B． 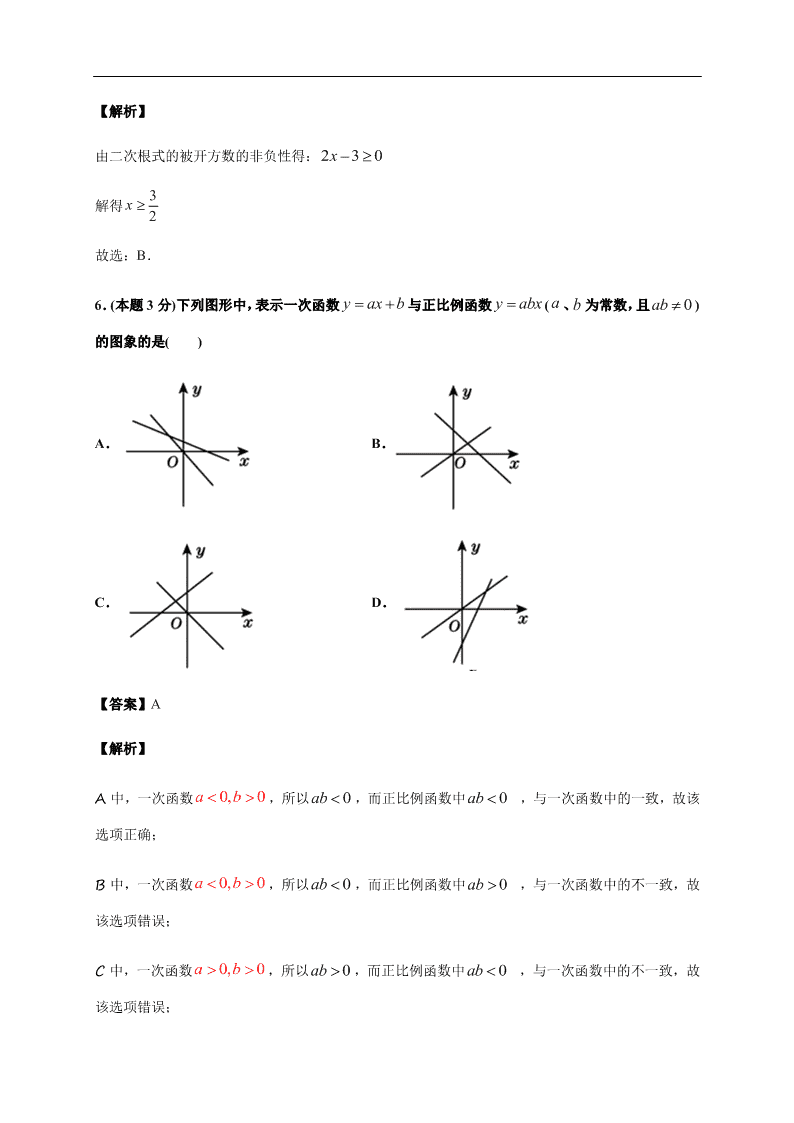6．(本题 3 分)下列图形中，表示一次函数 y ax b与正比例函数 y abx ( a 、b 为常数，且 0ab  ) 的图象的是( ) A． B． C． D． 【答案】A 【解析】 A 中，一次函数 0,0ab，所以 0ab  ，而正比例函数中 ，与一次函数中的一致，故该 选项正确； B 中，一次函数 ，所以 ，而正比例函数中 0ab  ，与一次函数中的不一致，故 该选项错误； C 中，一次函数 0, 0ab，所以 ，而正比例函数中 ，与一次函数中的不一致，故 该选项错误； D 中，一次函数 0 , 0ab，所以 0ab  ，而正比例函数中 0ab  ，与一次函数中的不一致，故 该选项错误； 7．(本题 3 分)小李家距学校 3 千米，中午 12 点他从家出发到学校，途中路过文具店买了些学习用 品，12 点 50 分到校．下列图象中能大致表示他离家的距离 S（千米）与离家的时间 t（分钟）之间 的函数关系的是（ ） A． B． C． D． 【答案】C 【解析】 ∵小李距家 3 千米，∴离家的距离随着时间的增大而增大． ∵途中在文具店买了一些学习用品，∴中间有一段离家的距离不再增加，综合以上 C 符合． 故选 C． 8．(本题 3 分)在下表中，设 x 表示乘公共汽车的站数，y 表示应付的票价（元） x（站） 1 2 3 4 5 6 7 8 9 10 y（元） 1 1 1 2 2 3 3 3 4 4 根据此表，下列说法正确的是（ ） A．y 是 x 的函数 B．y 不是 x 的函数 C．x 是 y 的函数 D．以上说法都不对 【答案】A 【解析】 解：根据题意：对于 x 的每一个取值，y 都有唯一确定的值， 故 y 是 x 的函数． 故选：A． 9．(本题 3 分)已知    1122 ,1,1,PyPy 是一次函数 1yx   的图象上的两个点，则 12,yy的大小 关系是（ ） A． 12yy B． 12yy C． 12yy D．不能确定 【答案】C 【解析】 解：∵P1（-1，y1）、 P2（1，y2）是 y=-x-1 的图象上的两个点， ∴y1=1-1=0，y2=-1-1=-2， ∵0＞-2， ∴y1＞y2． 故选：C． 10．(本题 3 分)甲、乙两同学从 A 地出发，骑自行车在同一条路上行驶到 B 地，他们离出发地的距 离 s（千米）和行驶时间 t（小时）之间的函数关系图象如图所示，根据图中提供的信息，有下列说 法： （1）他们都行驶了 18 千米； （2）甲在途中停留了 0.5 小时； （3）乙比甲晚出发了 0.5 小时； （4）相遇后，甲的速度小于乙的速度； （5）甲、乙两人同时到达目的地 其中符合图象描述的说法有（ ） A．2 个 B．3 个 C．4 个 D．5 个 【答案】C 【解析】 解：（1）根据统计图，他们都行驶了 18 千米到达目的地，故（1）正确； （2）甲行驶了 0.5 小时，在途中停下，一直到 1 小时，因此在途中停留了 0.5 小时，故（2）正确； （3）甲行驶了 0.5 小时，乙才出发，因此乙比甲晚出发了 0.5 小时，故（3）正确； （4）根据统计图，很明显相遇后，甲的速度小于乙的速度，故（4）正确； （5）甲行驶了 2.5 小时到达目的地，乙用了 2-0.5=1.5 小时到达目的地，故（5）错误． 综上所述，正确的说法有 4 个． 故选：C． 第 II 卷（非选择题) 二、填空题(共 15 分) 11．(本题 3 分)函数 3 1 xy x   中，自变量 x 的取值范围是_____． 【答案】x≥﹣3 且 x≠1 【解析】 由题意得， x ＋3≥0 且 −1≠0， 解得 ≥−3 且 ≠1． 故答案为 ≥−3 且 ≠1． 12．(本题 3 分)如果将直线 1 2yx 沿 y 轴向下平移 2个单位，那么平移后所得直线的表达式是______． 【答案】 1 22yx 【解析】 解：原直线的 k= 1 2 ，b=0；向下平移 2 个单位长度，得到了新直线， 那么新直线的 k= ，b=0-2=-2． ∴新直线的解析式为 y= x-2． 故答案是：y= x-2． 13．(本题 3 分)已知一次函数的图象过点（3，5）与点（-4，-9），则这个一次函数的解析式为 ____________. 【答案】 21.yx 【解析】 解：设一次函数的解析式为： y kx b， 35 49 kb kb       解得： 2 1 k b    所以这个一次函数的解析式为： 2 1 .yx 故答案为： 14．(本题 3 分)购买单价为每支 2 元的圆珠笔，总金额 y （元）与铅笔数 n （支）的关系式可表示为 y  _______，其中，______是变量． 【答案】 2yn 、 【解析】 解：由题意得： 2.yn 其中 是自变量， 是因变量． 故答案为： 2,.ynny 、 15．(本题 3 分)如果点 A(1，n)在一次函数 y＝3x﹣2 的图象上，那么 n＝_____． 【答案】1 【解析】 ∵点 A(1，n)在一次函数 y＝3x﹣2 的图象上， ∴n＝3×1﹣2＝1． 故答案为：1． 三、解答题(共 55 分) 16．(本题 6 分)已知正比例函数 2 3my mx  ，y 的值随 x 的值减小而减小，求 m 的值． 【答案】 2 【解析】 ∵ y 的值随 x 的值减小而减小， ∴ 0m  ， ∵正比例函数 2 3my mx  ， ∴ 2 31m ， ∴ 2m  17．(本题 8 分)小明在游乐场坐过山车，某一分钟内过山车高度 h（米）与时间 t （秒）之间的函数 图象如图所示，请结合图象回答： （1）过山车所达到的最大高度是多少？ （2）请描述 41 秒后，高度 h （米）随时间 （秒）的变化情况 【答案】（1）过山车所达到的最大高度是98 米；（2）当 4153 t 时，高度 （米）随时间 （秒） 的增大而增大，当5360t 时，高度 （米）随时间 （秒）的增大而减小． 【解析】 解：（1）由图可知，过山车所达到的最大高度是 米． （2）由图可知，当 时，高度 （米）随时间 （秒）的增大而增大． 当 5 3 6 0t 时，高度 h （米）随时间 t （秒）的增大而减小． 18．(本题 9 分)（1）先列表，再画出函数 21yx的图象． （2）若直线 向下平移了 1 个单位长度，直接写出平移后的直线表达式. 【答案】（1）见解析；（2） 2yx 【解析】 解：（1）列表如下： 描点并连线： （2）直线 向下平移了 1 个单位长度得到 ． 19．(本题 10 分)综合与探究： 如图，直线 1l 的表达式为 33yx   ，与 x 轴交于点 C ，直线 2l 交 轴于点 A ， 4OA  ， 与 交于点 B ，过点 作 B D x 轴于点 D ， 3BD  ． （1）求点 的坐标； （2）求直线 的表达式； （3）求 ABCS  的值； （4）在 轴上是否存在点 P ，使得 2ABPABCSS ？若存在，请直接写出点 的坐标；若不存在， 请说明理由． 【答案】（1）  1 ,0C ；（ 2） 3 62yx；（ 3） 9 2 ABCS ；（ 4）存在，点  2,0P  或  10 ,0 【解析】 解：  1 令 中 0y  得： 330x ， 解得 1x  ，  1,0C  2 直线 交 轴于点 ,4A OA   4,0A B D xQ 轴， 3BD   点 B 的纵坐标为 3 在 33yx   中， 当 3y  时， 3 3 3x    ，解得 2x  ，  2 , 3B 设直线 2l 的表达式为 ( 0 )y k x b k   ， 将    4,0,2,3AB 代入得 40 23 kb kb      ，解得 3 2 6 k b     直线 的表达式为 3 62yx      34,0,1,0AC 3AC 轴， 193322ABCS  4 92 2 92ABP ABCSS   Q ， 13922ABPS AP BD AP     6AP  4,0AQ ，点 P 在 x 轴上  2,0P  或 10,0 所以存在点  2 ,0P  或  10 ,0 使得 2ABPABCSS 20．(本题 10 分)已知直线 :l y k x b 与直线 2yx 平行，且直线 l 过点（2,8），求直线 与 x 轴 的交点坐标 【答案】（ 2 ，0） 【解析】 ∵直线 ： y k x b与直线 2yx 平行， ∴ 2k  ， ∵直线 过点(2，8)， ∴ 8 2 2 b   ， ∴ 4b  ． ∴直线 的解析式为 24yx， 当 0y  时，解得： 2x  ， ∴直线 与 轴的交点坐标为( ，0)． 21．(本题 12 分)某通讯移动通讯公司手机费用有 A、B 两种计费标准，如下表： 月租费（元/部） 通讯费（元/分钟） 备注 A 种收费标准 50 0.4 通话时间不足 1 分钟按 1 分钟计算 B 种收费标准 0 0.6 设某用户一个月内手机通话时间为 x 分钟，请根据上表解答下列问题： （1）分别写出按 A 类、B 类收费标准，该用户应缴纳手机费用的关系式； （2）如果该用户每月通话时间为 300 分钟，应选择哪种收费方式？说说你的理由； （3）如果该用户每月手机费用不超过 90 元，应选择哪种收费方式？说说你的理由； 【答案】（1）WA=50+0.4x；WB=0.6x；（ 2）应选择 A 种计费标准，更合适更省钱；（3）应该选用 B 种计费标准． 【解析】 解：（1）设按 A 类、B 类收费标准，该用户应缴纳手机费用为 WA、WB，由题意得： WA=50+0.4x；WB=0.6x； （2）该用户每月通话时间为 300 分钟时， 按 A 类收费标准，该用户应缴纳手机费用为：WA=50+0.4×300=170（元）； 按 B 类收费标准，该用户应缴纳手机费用为：WB=0.6×300=180（元）； 因为 WA＜WB，所以应选择 A 种计费标准，更合适更省钱； （3）该用户每月手机费用不超过 90 元时，选用 A 种计费标准通话时长最长为： （90-50）÷0.4=100（分钟）； 选用 B 种计费标准通话时长最长为：90÷0.6=150（分钟）， 因为选用 A 种计费标准通话最长时长＜选用 B 种计费标准通话最长时长， 所以应该选用 B 种计费标准． 故答案为：（1）WA=50+0.4x；WB=0.6x；（ 2）应选择 A 种计费标准，更合适更省钱；（3）应该选用 B 种计费标准．