人教版八年级上册数学期末测试题附答案1 7页

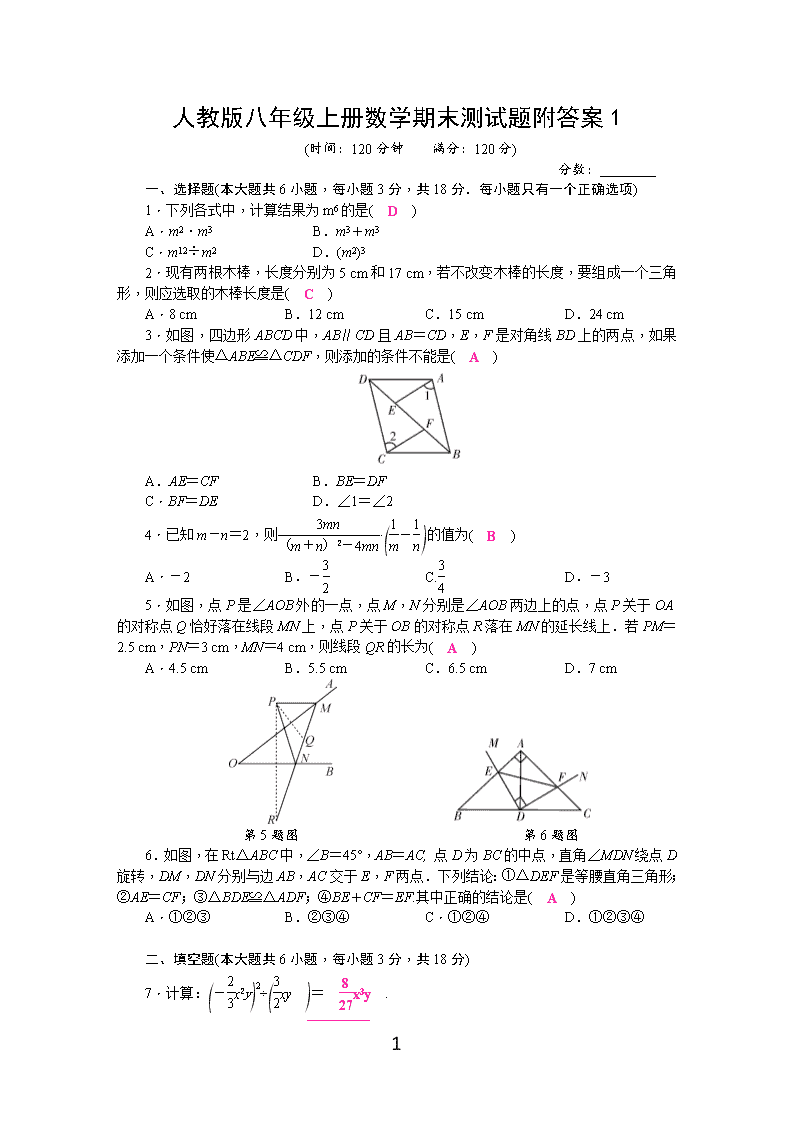
人教版八年级上册数学期末测试题附答案1‎ ‎(时间：120分钟　　满分：120分)‎ 分数：________‎ 一、选择题(本大题共6小题，每小题3分，共18分．每小题只有一个正确选项)‎ ‎1．下列各式中，计算结果为m6的是(　D　)‎ A．m2·m3 B．m3＋m3‎ C．m12÷m2 D．(m2)3‎ ‎2．现有两根木棒，长度分别为5 cm和17 cm，若不改变木棒的长度，要组成一个三角形，则应选取的木棒长度是(　C　)‎ A．8 cm B．12 cm C．15 cm D．24 cm ‎3．如图，四边形ABCD中，AB∥CD且AB＝CD，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件不能是(　A　)‎ A．AE＝CF B．BE＝DF C．BF＝DE D．∠1＝∠2‎ ‎4．已知m－n＝2，则·的值为(　B　)‎ A．－2 B．－ C. D．－3‎ ‎5．如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM＝2.5 cm，PN＝3 cm，MN＝4 cm，则线段QR的长为(　A　)‎ A．4.5 cm B．5.5 cm C．6.5 cm D．7 cm ‎ ‎ 第5题图　　 第6题图 ‎6．如图，在Rt△ABC中，∠B＝45°，AB＝AC, 点D为BC的中点，直角∠MDN绕点D旋转，DM，DN分别与边AB，AC交于E，F两点．下列结论：①△DEF是等腰直角三角形；②AE＝CF；③△BDE≌△ADF；④BE＋CF＝EF.其中正确的结论是(　A　)‎ A．①②③ B．②③④ C．①②④ D．①②③④‎ 二、填空题(本大题共6小题，每小题3分，共18分)‎ ‎7．计算：÷＝ x3y .‎ 7‎ ‎8．当m＝ 2 时，此分式方程 ＝无解．‎ ‎9．在Rt△ABC中，已知∠ACB＝90°，AB边的垂直平分线交AB于点E，交BC于点D，且∠ADC＝30°，BD＝18 cm，则AC的长为 9 cm.‎ ‎10．已知AD是△ABC的角平分线，CE是△ABC的高，∠BAC＝60°，∠BCE＝40°，则∠ADB的度数为 100° .‎ ‎11．如图，已知等腰△ABC中，AB＝AC，∠BAC＝120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP＝OC，则∠APO＋∠DCO的度数为 30° ．‎ ‎ ‎ 第11题图　　 第12题图 ‎12．★如图，在平面直角坐标系中，点A的坐标为(1，0)，点B的坐标为(1，4)，点C的坐标为(－2，6)．如果存在点D，使得△ABD与△ABC全等，那么点D的坐标为 (4，6)或(－2，－2)或(4，－2) ．(写出所有可能的情况)‎ 三、(本大题共5小题，每小题6分，共30分)‎ ‎13．化简：‎ ‎(1)(6x4－8x3)÷(－2x2)－(3x＋2)(1－x)；‎ 解：原式＝－3x2＋4x－(3x－3x2＋2－2x)‎ ‎＝－3x2＋4x－3x＋3x2－2＋2x ‎＝3x－2.‎ ‎(2)÷.‎ 解：原式＝· ‎＝· ‎＝· ‎＝2m＋6.‎ ‎14．如图，在△ABC中，AB＝AC，AD是BC边上的中线，E是AC边上的一点，且∠CBE＝∠CAD，求证：BE⊥AC.‎ 7‎ 证明：∵AB＝AC，AD是BC边上的中线，‎ ‎∴AD⊥BC，‎ ‎∴∠CAD＋∠C＝90°.‎ ‎∵∠CBE＝∠CAD，‎ ‎∴∠CBE＋∠C＝90°，‎ ‎∴∠BEC＝90°，即BE⊥AC.‎ ‎15．分解因式：‎ ‎(1)a(a－b)2－ab(b－a)2；‎ 解：原式＝a(a－b)2(1－b)．‎ ‎(2)1－a2－4b2＋4ab.‎ 解：原式＝(1＋a－2b)(1－a＋2b)．‎ ‎16．解方程：＋＝.‎ 解：方程为－＝，‎ 在方程两边同乘(x＋2)(x－2)，得 ‎(x－2)2－16＝(x＋2)2，‎ 解得x＝－2，‎ 经检验，当x＝－2时，(x＋2)(x－2)＝0，‎ ‎∴原方程无解．‎ ‎17．先化简，再求值：‎ ÷，其中a＝(3－π)0＋.‎ 解：原式＝· ‎＝· ‎＝2a＋6.‎ ‎∵a＝(3－π)0＋＝1＋4＝5，‎ ‎∴原式＝2×5＋6＝16.‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎18．用无刻度的直尺作图，保留作图痕迹．‎ ‎(1)在图①中，BD是△ABC的角平分线，作△ABC的内角∠C的平分线；‎ ‎(2)在图②中，AD是∠BAC的角平分线，作△ABC的∠BCA相邻的外角的角平分线．‎ 7‎ ‎　　　①　　　　　　　　　　　②　　‎ 解：(1)如图①，线段CE即为所求．‎ ‎(2)如图②，射线CD即为所求．‎ ‎19．如图，在四边形ABCD中，∠B＝90°，DE∥AB，DE交BC于E，交AC于F，DE＝BC，∠CDE＝∠ACB＝30°.‎ ‎(1)求证：△FCD是等腰三角形；‎ ‎(2)若AB＝4，求CD的长．‎ ‎(1)证明：∵DE∥AB，‎ ‎∠B＝90°，∴∠DEC＝90°，‎ ‎∴∠DCE＝90°－∠CDE＝60°，‎ ‎∴∠DCF＝∠DCE－∠ACB ‎＝30°，‎ ‎∴∠CDE＝∠DCF，‎ ‎∴DF＝CF，‎ ‎∴△FCD是等腰三角形．‎ ‎(2)解：在△ACB和△CDE中，‎ ‎∠B＝∠DEC＝90°，BC＝DE，∠ACB＝∠CDE，‎ ‎∴△ACB≌△CDE，∴AC＝CD.‎ 在Rt△ABC中，∠B＝90°，∠ACB＝30°，‎ AB＝4，∴AC＝2AB＝8，∴CD＝8.‎ ‎20．(达州中考)设A＝÷.‎ ‎(1)化简A；‎ ‎(2)当a＝3时，记此时A的值为f(3)；当a＝4时，记此时A的值为f(4)；….‎ 解关于x的不等式：－≤f(3)＋f(4)＋…＋f(11)，并将解集在数轴上表示出来．‎ 解：(1)A＝÷ ‎＝÷ ‎＝· 7‎ ‎＝· ‎＝.‎ ‎(2)∵a＝3时，f(3)＝＝；‎ a＝4时，f(4)＝＝；‎ a＝5时，f(5)＝＝；‎ ‎…‎ ‎∴－≤f(3)＋f(4)＋…＋f(11)，‎ 即－≤＋＋…＋，‎ ‎∴－≤－，‎ ‎∴－≤，‎ 解得x≤4.‎ ‎∴原不等式的解集是x≤4，在数轴上表示如图所示．‎ 五、(本大题共2小题，每小题9分，共18分)‎ ‎21．某商店购进A，B两种商品，购买1个A商品比购买1个B商品多花10元，并且花费300元购买A商品和花费100元购买B商品的数量相等．‎ ‎(1)求购买一个A商品和一个B商品各需要多少元；‎ ‎(2)商店准备购买A，B两种商品共80个，若A商品的数量不少于B商品数量的4倍，并且购买A，B商品的总费用不低于1 000元且不高于1 050元，那么商店有哪几种购买方案？‎ 解：(1)设买一个B商品需要x元，则购买一个A商品需要(x＋10)元，则 ＝，‎ 解得x＝5.‎ 经检验，x＝5是原分式方程的解．‎ ‎∴购买一个A商品需要15元，购买一个B商品需要5元．‎ ‎(2)设买A商品y个，则买B商品(80－y)个．‎ 由题意得 解得64≤y≤65.‎ ‎∴有两种方案：‎ ‎①购买A商品64个，B商品16个；‎ ‎②购买A商品65个，B商品15个．‎ ‎22.如图①，在△CAB和△CDE中，CA＝CB，CD＝CE，∠ACB＝∠DCE＝α，‎ 7‎ 连接AD，BE.‎ ‎(1)求证：△ACD≌△BCE；‎ ‎(2)如图②，当α＝90°时，取AD，BE的中点P，Q，连接CP，CQ，PQ，判断△CPQ的形状，并加以证明．‎ ‎ ‎ ‎(1)证明：∵∠ACB＝∠DCE，‎ ‎∴∠ACB＋∠BCD＝∠DCE＋∠BCD，‎ 即∠ACD＝∠BCE.‎ ‎∵CA＝CB，CD＝CE，‎ ‎∴△ACD≌△BCE(SAS)．‎ ‎(2)解：△CPQ是等腰直角三角形．‎ 证明：由(1)知△ACD≌△BCE，‎ ‎∴∠CAD＝∠CBE，AD＝BE.‎ ‎∵P，Q分别是AD，BE的中点，‎ ‎∴AP＝AD，BQ＝BE，‎ ‎∴AP＝BQ.∵CA＝CB，‎ ‎∴△ACP≌△BCQ(SAS)，‎ ‎∴CP＝CQ，∠ACP＝∠BCQ，‎ ‎∴∠PCQ＝∠PCB＋∠BCQ ‎＝∠PCB＋∠ACP ‎＝∠ACB.‎ ‎∵∠ACB＝α＝90°，‎ ‎∴∠PCQ＝90°，‎ ‎∴△CPQ是等腰直角三角形．‎ 六、(本大题共12分)‎ ‎23．如图①，直线AB与x轴的负半轴、y轴的正半轴分别交于A，B，OA，OB的长分别为a，b，且满足a2－2ab＋b2＝0.‎ ‎(1)判断△AOB的形状，并说明理由；‎ ‎(2)如图②，过坐标原点作直线OQ交直线AB于第二象限的点Q，过A，B两点分别作AM⊥OQ，BN⊥OQ，若AM＝7，BN＝4，求MN的长；‎ ‎(3)如图③，E为AB上一动点，以AE为斜边作等腰直角三角形ADE，P为BE的中点，延长DP至F，使PF＝DP，连接PO，BF，试问DF，PO是否存在确定的位置关系和数量关系？写出你的结论并证明．‎ 7‎ 解：(1)△AOB是等腰直角三角形，理由略．‎ ‎(2)∵AM⊥OQ，BN⊥OQ，‎ ‎∴∠AMO＝∠ONB＝90°，‎ ‎∴∠MAO＋∠MOA＝90°.∵∠AOB＝90°，‎ ‎∴∠MOA＋∠NOB＝90°，‎ ‎∴∠MAO＝∠NOB.∵OA＝OB，‎ ‎∴△AMO≌△ONB.‎ ‎∴ON＝AM＝7，OM＝BN＝4，‎ ‎∴MN＝ON－OM＝3.‎ ‎(3)OP＝DF，OP⊥DF.‎ 证明：连接OD，OF，∵P为BE的中点，‎ ‎∴BP＝EP.∵∠BPF＝∠EPD，PF＝PD，‎ ‎∴△BPF≌△EPD，‎ ‎∴BF＝ED，∠FBP＝∠DEP.‎ ‎∵△ADE是等腰直角三角形，‎ ‎∴AD＝ED，∠DEA＝∠DAE＝45°，‎ ‎∴BF＝AD，∠FBP＝∠DEP＝180°－45°＝135°.‎ ‎∵△AOB是等腰直角三角形，‎ ‎∴OB＝OA，∠ABO＝∠BAO＝45°，‎ ‎∴∠FBO＝∠FBP－∠ABO＝135°－45°＝90°，∠DAO＝∠DAE＋∠BAO＝45°＋45°＝90°，‎ ‎∴∠FBO＝∠DAO.∵OB＝OA，BF＝AD，∴△FBO≌△DAO，∴∠FOB＝∠DOA，OD＝OF，‎ ‎∴∠DOF＝∠DOB＋∠BOF ‎＝∠DOB＋∠DOA ‎＝∠AOB＝90°，‎ ‎∴△DOF是等腰直角三角形．∵PF＝DP，‎ ‎∴OP⊥DF，∠POD＝∠POF＝∠DOF＝45°，‎ ‎∴△POD，△POF都是等腰直角三角形，‎ ‎∴OP＝PD＝PF，‎ ‎∴OP＝DF.‎ 7‎