_2020-2021学年度江苏省淮安市第一中学九年级第一学期 第十八周周末提优训练 28页

第 1 页，共 28 页 苏科版 2020-2021 学年度江苏省淮安市第一中学九上第十 八周周末提优训练 班级：___________姓名：___________得分：___________ 一、选择题 1. 甲、乙两人一周五天工作日每天生产合格产品的个数如下表所示，其中 a 为自然 数．则下列说法不正确的是 甲 11 4 7 6 7 乙 8 6 7 7 A. 甲、乙的中位数一定相同 B. 当 ‸ 㔳 时，甲的方差大于乙的方差 C. 甲、乙的众数一定相同 D. 甲的平均数一定大于乙的平均数 2. 袋中装有 5 个红球、6 个黑球、7 个白球，从袋中摸出 15 个球，摸出的球中恰好有 3 个红球的概率是 A. 1 B. 1 1㔳 C. 1㔳 D. 2 . 对于一元二次方程 2 ܾ ‸ 㔳 㔳 ，下列说法． 若 ܾ ‸ 㔳 ，则 ܾ 2 㔳 ； 若方程 2 ‸ 㔳 有两个不相等的实根，则方程 2 ܾ ‸ 㔳 必有两个不 相等的实根； 若 c 是方程 2 ܾ ‸ 㔳 的一个根，则一定有 ܾ 1 ‸ 㔳 成立； 若 㔳 是一元二次方程 2 ܾ ‸ 㔳 的根，则 ܾ 2 ‸ 2㔳 ܾ 2 其中正确的 A. 只有 B. 只有 C. D. 只有 . 如图，A、B、C、D、E 是 上的 5 等分点，连接 AC、CE、EB、BD、DA，得到一个五角星图形和五 第 2 页，共 28 页 边形 onot. 有下列 3 个结论： ， oh ‸ h h ， ‸ o ‸ o. 其中正确的结论是 A. B. C. D. . 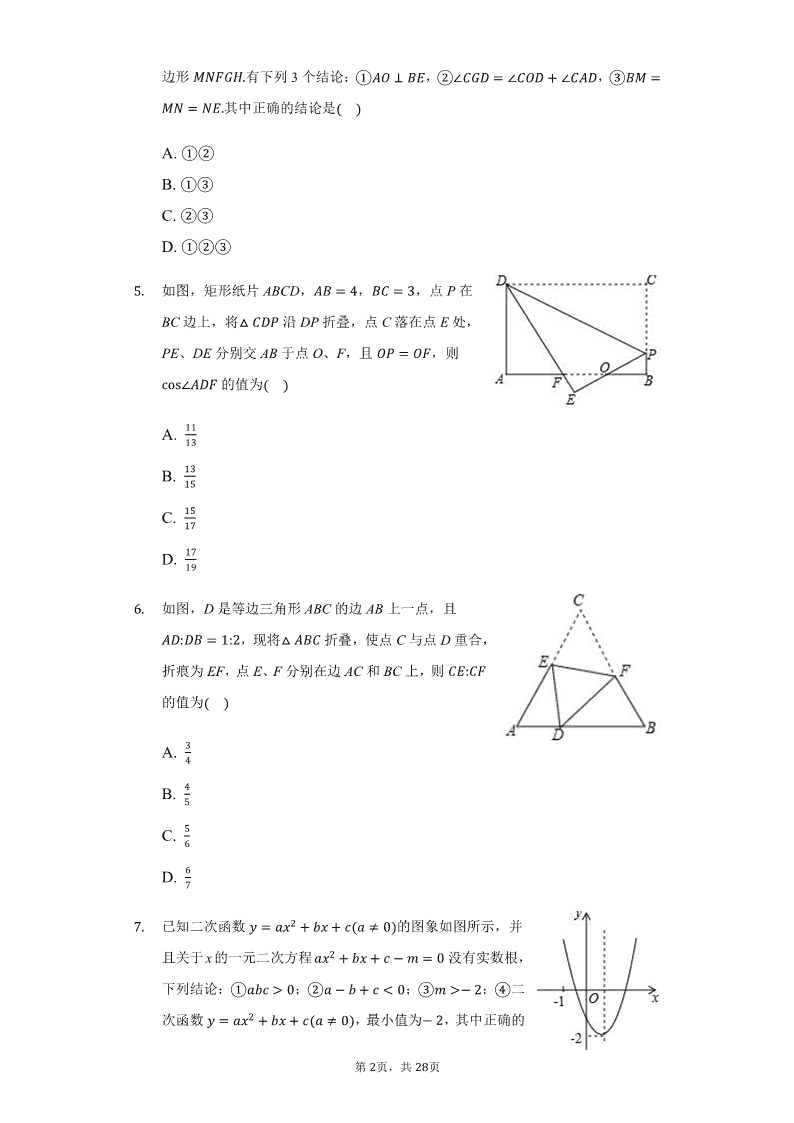如图，矩形纸片 ABCD， ‸ ， ‸ ，点 P 在 BC 边上，将 h䁨 沿 DP 折叠，点 C 落在点 E 处， PE、DE 分别交 AB 于点 O、F，且 䁨 ‸ n ，则 coshn 的值为 A. 11 1 B. 1 1 C. 1 1 D. 1 1 . 如图，D 是等边三角形 ABC 的边 AB 上一点，且 hh ‸ 12 ，现将 折叠，使点 C 与点 D 重合， 折痕为 EF，点 E、F 分别在边 AC 和 BC 上，则 n的值为 A. B. C. D. . 已知二次函数 ‸ 2 ܾ 㔳 的图象如图所示，并 且关于x 的一元二次方程 2 ܾ ‸ 㔳 没有实数根， 下列结论： ܾ ܿ 㔳 ； ܾ ܿ 㔳 ； ܿ 2 ； 二 次函数 ‸ 2 ܾ 㔳 ，最小值为 2 ，其中正确的 第 页，共 28 页 个数有 A. 1 B. 2 C. 3 D. 4 8. 如图，将矩形 OABC 置于平面直角坐标系中，点 A 的坐标为 㔳 ，点 C 在 x 轴上，点 h 1 在 BC 上，将矩形 OABC 沿 AD 折叠压平，使点 B 落在坐标 平面内，设点 B 的对应点为点 . 若抛物线 ‸ 2 1㔳 㔳 且 a 为常数 的顶点落在 h 的 内部，则 a 的取值范围是 A. 2 ܿ ܿ 1 2㔳 B. 2 ܿ ܿ 11 2㔳 C. 11 2㔳 ܿ ܿ D. ܿ ܿ 1 2㔳 二、填空题 . 已知一元二次方程 2 2 ‸ 㔳 的两个实数根为 1 ， 2 ，则 1 12 1 的值 是______． 1㔳. 如图，AB 是以点 O 为圆心的圆形纸片的直径，弦 h 于点 E， ‸ 1㔳 ， ‸ . 将阴影部分沿着弦 AC 翻折压 平，翻折后，弧 AC 对应的弧为 G，则点 O 与弧 G 所在圆 的位置关系为______． 11. 如图，二次函数 ‸ 1 2 8 1 的图象与 x 轴交于 A、B 两点 点 A 在点 B 的左边 ，与 y 轴交于点 C，其 对称轴与 x 轴交于点 D，若 P 为 y 轴上的一个动点，连 接 PD，则 䁨 䁨h 的最小值为______． 12. 如图，在 中，点 1 ， 1 ， 1 分别是 AC，BC， AB 的中点，连接 11 ， 11 ，四边形 111 的 面积记作 1 ；点 2 ， 2 ， 2 分别是 1 ， 1 ， 11的中点，连接 22 ， 22 ，四边形 2211 的面 第 页，共 28 页 积记作 2 ，按此规律进行下去，若 ‸ ，则 2㔳2㔳 ‸ ______． 1. 对某条线段的长度进行了 3 次测量，得到 3 个结果 单位： . ， 1㔳.1 ， 1㔳.㔳 ， 若用 a 作为这条线段长度的近似值，当 ‸ ______mm 时， . 2 1㔳.1 2 1㔳.㔳 2 最小．对另一条线段的长度进行了 n 次测量，得到 n 个结果 单位： 1 ， 2 ， ， ，若用 x 作为这条线段长度的近似值，当 ‸ ______mm 时， 1 2 2 2 2 最小． 1. 二次函数 ‸ 1 2 2 与反比例函数 ‸ 2 的图象如图所示，试根据图像回答： 不等式 1 2 2 2 x2 㔳 的解集是 ． 三、解答题 1. 在平面直角坐标系 xOy 中，给出如下定义：若点 P 在图形 M 上，点 Q 在图形 N 上， 如果 PQ 两点间的距离有最小值，那么称这个最小值为图形 M，N 的“近距离”， 记为 o. 特别地，当图形 M 与图形 N 有公共点时， o ‸ 㔳. 已知 㔳 ， 㔳 ， 2㔳 ， 1 点 A，点 ‸ ______， 点 A，线段 ‸ ______； 2 半径为 r， 当 ‸ 1 时，求 与线段 AB 的“近距离” ，线段 ； 若 ‸ 1 ，则 ‸ ______． h 为 x 轴上一点， h 的半径为 1，点 B 关于 x 轴的对称点为点 ， h 与 的“近距离” h ܿ 1 ，请直接写出圆心 D 的横坐标 m 的取值范围． 第 页，共 28 页 1. 如图， o 于点 O， 为等腰直角三角形， ‸ 㔳 ，当 绕点 O 旋转时，记 ‸ 㔳 t t 㔳 ， ‸ ． 1 过点 B 作 o 交射线 ON 于点 C，作射线 CA 交射线 OM 于点 D． 依题意补全图形，求 h 的度数； 当 ‴ ‸ 时，求 OD 的长． 2 若 ON 上存在一点 P，且 䁨 ‸ 1㔳 ，作射线 PB 交射线 OM 于点 Q，直接写出 QP 长度的最大值． 1. 如图，AC 平分钝角 交过 B 点的直线于点 C，BD 平分 交 AC 于点 D， 且 h h ‸ 㔳 ． 1 求证： ； 2 点 F 是射线 BC 上一动点 点 F 不与点 B，C 重合 ，连接 AF，与射线 BD 相交 于点 P． 如图 1，若 ‸ ， n ，试探究线段 BF 与 CF 之间满足的数量关系； 第 页，共 28 页 如图 2，若 ‸ 1㔳 ， ‸ 㔳 ， n ‸ h ，求线段 BP 的长． 18. 小明根据学习函数的经验，对函数 ‸ 1 的图象与性质进行了探究． 下面是小明的探究过程，请补充完整： 1 函数 ‸ 1 的自变量 x 的取值范围是______． 2 下表列出了 y 与 x 的几组对应值，请写出 m，n 的值： ‸ ______， ‸ ______； x 2 1 1 2 1 1 1 2 1 2 3 4 y 1㔳 2 2 2 1㔳 m 2 2 2 n 1 如图，在平面直角坐标系 xOy 中，描出了以上表中各对对应值为坐标的点，根 据描出的点，画出该函数的图象； 结合函数的图象，请完成： 当 ‸ 1 时， ‸ ______． 写出该函数的一条性质______． 若方程 1 ‸ 有两个不相等的实数根，则 t 的取值范围是______． 第 页，共 28 页 19. 已知抛物线 ‸ 2 ܾ 㔳 与 x 轴交于 A、B 两点 点 A 在点 B 的左边 ，与 y 轴交于点 㔳 ， 顶点 D 的坐标为 1 ． 1 求抛物线的解析式． 2 在 y 轴上找一点 E，使得 为等腰三角形，请 直接写出点 E 的坐标． 点 P 是 x 轴上的动点，点 Q 是抛物线上的动点，是否存在点 P、Q，使得以点 P、 Q、B、D 为顶点，BD 为一边的四边形是平行四边形？若存在，请求出点 P、Q 坐 标；若不存在，请说明理由． 20. 如图 1 所示，已知直线 ‸ 与抛物线 ‸ 2 ܾ 分别交于 x 轴和 y 轴上同一点，交点分别是点 㔳 和点 㔳 ，且抛物线的对称轴为直线 ‸ ； 1 试确定抛物线的解析式； 2 在抛物线的对称轴上是否存在点 P，使 䁨 是直角三角形？若存在请直接写 出 P 点坐标，不存在请说明理由； 如图 2，点 Q 是线段 BC 上一点，且 ‴ ‸ 1㔳 2 ，点 M 是 y 轴上一个动点，求 ‴的最小周长． 第 8 页，共 28 页 第 页，共 28 页 答案和解析 1. C 解： 为自然数， t ， 甲、乙的中位数一定相同，都是 7，故 A 正确； 当 ‸ 㔳 时，甲的平均数 ‸ ，乙的平均数 ‸ .8 ， 甲 2 ‸ 1 11 2 2 2 2 2 ‸ .2 ， 乙 2 ‸ 1 8 .8 2 .8 2 .8 2 .8 2 .8 2 ‸ 㔳. ， 甲的方差大于乙的方差，故 B 正确； 为自然数， 不确定， 乙的众数不确定， 甲、乙的众数不一定相同，故 C 错误； 甲的平均数为 7，乙的平均数为 ܿ ， 甲的平均数一定大于乙的平均数，故 D 正确； 2. A 解：设摸出的 15 个球中有 x 个红球、y 个黑球、z 个白球，则 x，y，z 都是正整数，且 t ， t ， t ， ‸ 1 ． t 1 ， 可取值 2，3，4，5． 当 ‸ 2 时，只有一种可能，即 ‸ ， ‸ ； 当 ‸ 时， ‸ 12 ，有 2 种可能， ‸ ， ‸ 或 ‸ ， ‸ ； 当 ‸ 时， ‸ 11 ，有 3 种可能， ‸ ， ‸ 或 ‸ ， ‸ 或 ‸ ， ‸ ； 当 ‸ 时， ‸ 1㔳 ，有 4 种可能， ‸ ， ‸ 或 ‸ ， ‸ 或 ‸ ， ‸ 或 ‸ ， ‸ ． 共有 1 2 ‸ 1㔳 种可能的摸球结果，其中摸出的球中恰好有 3 个红球的结果 第 1㔳 页，共 28 页 有 2 种， 所求的概率为： 2 1㔳 ‸ 1 ． 3. B 解： 若 ܾ ‸ 㔳 ，则 ‸ 1 是方程 2 ܾ ‸ 㔳 的解， 由一元二次方程的实数根与判别式的关系可知 ‸ ܾ 2 㔳 ，故 正确； 方程 2 ‸ 㔳 有两个不相等的实根， ‸ 㔳 ܿ 㔳 ܿ 㔳则方程 2 ܾ ‸ 㔳 的判别式 ‸ ܾ 2 ܿ 㔳 方程 2 ܾ ‸ 㔳 必有两个不相等的实根，故 正确； 是方程 2 ܾ ‸ 㔳 的一个根， 则 2 ܾ ‸ 㔳 ܾ 1 ‸ 㔳若 ‸ 㔳 ，等式仍然成立 但 ܾ 1 ‸ 㔳 不一定成立，故 不正确； 若 㔳 是一元二次方程 2 ܾ ‸ 㔳 的根， 则由求根公式可得： 㔳 ‸ ܾ ܾ2 2 或 㔳 ‸ ܾ ܾ2 2 2㔳 ܾ ‸ ܾ 2 或 2㔳 ܾ ‸ ܾ 2 ܾ 2 ‸ 2㔳 ܾ 2 故 正确． 4. A 解： 、B、C、D、E 是 上的 5 等分点， ‸ ， ，故 正确； 、B、C、D、E 是 上的 5 等分点， 第 11 页，共 28 页 h 的度数 ‸ 㔳 ‸ 2 h ‸ 2 h ‸ 2h h ‸ ； 连接 CD 、B、C、D、E 是 上的 5 等分点， ‸ h ‸ ‸ h ， h ‸ h ‸ h ‸ ， oh ‸ 1㔳8 ， oh ‸ h h ，故 正确； 连接 AB，AE， 则 ‸ ‸ o ‸ o ‸ ， ‸ ， ≌ o ， ‸ o ‸ ‸ o ， o ‸ ， o ， 错误． 5. C 解：根据折叠，可知： h䁨≌ h䁨 ， h ‸ h ‸ ， 䁨 ‸ 䁨 ． 在 n 和 䁨 中， n ‸ 䁨 ‸ ‸ 㔳 䁨 ‸ n ， n≌ 䁨 ， ‸ ， n ‸ 䁨 ． 第 12 页，共 28 页 设 n ‸ ，则 䁨 ‸ ， hn ‸ h n ‸ ， 又 n ‸ n ‸ 䁨 ‸ 䁨 ‸ 䁨 ， 䁨 ‸ 䁨 ‸ ， n ‸ n ‸ 1 ． 在 hn 中， n 2 h 2 ‸ hn 2 ，即 1 2 2 ‸ 2 ， 解得： ‸ ， hn ‸ ‸ 1 ， coshn ‸ h hn ‸ 1 1 ． 6. B 解：设 h ‸ ，则 h ‸ 2 ， 为等边三角形， ‸ ‸ ， ‸ ‸ ‸ 㔳 ， 由翻折的性质， hn ‸ ‸ 㔳 ， h nh ‸ 12㔳 ， 又 h h ‸ 12㔳 ， nh ‸ h ， h hn ， 由翻折的性质，得 ‸ h ， n ‸ hn ， h 的周长 ‸ h h ‸ h ‸ ， hn 的周长 ‸ h n hn ‸ ， h 与 hn 的相似比为 4：5， ： n ‸ h ： hn ‸ ：5． 7. B 解： 对称轴在 y 轴右侧，则 ܾ ܿ 㔳 ，而 ܿ 㔳 ，故 ܾ ܿ 㔳 正确，符合题意； 当 ‸ 1 时， ‸ ܾ ܿ 㔳 ，故原选项错误，不符合题意； 关于 x 的一元二次方程 2 ܾ ‸ 㔳 没有实数根，即 ‸ 2 ܾ 与 ‸ 没有交点，故 ܿ 2 ，原选项错误，不符合题意； 从图象看二次函数 ‸ 2 ܾ 㔳 的最小值为 2 ，故符合题意； 第 1 页，共 28 页 8. B 解：如图， 过点 E 作 轴于 M，交 BC 延长线于 N，过点 E 作 n 于 F，EF 分别与 AD、 OC 交于点 G、H， ‸ ho ‸ 㔳 ， ‸ ho ， ho ， o ‸ ho ， 设 ‸ o ‸ ， ‸ ， o ‸ o ‸ ， ho ‸ o h ‸ ， 代入 得， ‸ ， 根据勾股定理得， 2 2 ‸ 2 ， 由 得 1 ‸ ， 1 ‸ 㔳 舍 ， 2 ‸ 2 ， 2 ‸ ， 点 A 的坐标为 㔳 ，点 h 1 ， h ‸ h ‸ ， ‸ ， n ‸ 2 ， 2 1 ． 过点 D 作 h䁨 n 于点 P， 则 䁨 ‸ 䁨t t ‸ h t ‸ 2 ， no ‸ h ‸ 㔳 ， no ‸ h ， no h ． n ‸ no h ， 即： 2 ‸ no ， no ‸ 2 ． 第 1 页，共 28 页 o ‸ n no ‸ ． 点 G 的纵坐标为 2． ‸ 2 1㔳 ‸ 2 2 1㔳 2㔳 ， 此抛物线 ‸ 2 1㔳 的顶点必在直线 ‸ 2 上． 又 抛物线的顶点落在 h 的内部， 此抛物线的顶点必在 EG 上． 1 ܿ 1㔳 2㔳 ܿ 2 ， 2 ܿ ܿ 11 2㔳 ． 9. 解： 一元二次方程 2 2 ‸ 㔳 的两个实数根为 1 ， 2 ， 1 2 ‸ ， 1 2 ‸ 2 ， 1 12 1 ‸ 1 2 1 2 1 ‸ 2 1 ‸ ． 10. 点在圆外 解：过 O 作 ，交 于 F，交弧 G 于 H，连 接 OC， 为 的直径， ‸ 1㔳 ， ‸ ‸ o ‸ ‸ ， ‸ ， ‸ 2 ， 在 中，由勾股定理得： ‸ 2 2 ‸ 2 2 2 ‸ 21 ， 在 中， ‸ 2 2 ‸ 2 21 ‸ 㔳 ， n ， ‸ 1 2 ‸ 㔳 2 ， 由勾股定理得： ‸ 2 2 ‸ 2 㔳 2 2 ‸ 㔳 2 ， 由折叠得：弧 G 所在圆与圆 O 是等圆， 弧 G 所在圆的半径为 5， 第 1 页，共 28 页 t ‸ n ‸ 㔳 2 ， 㔳 2 ܿ 㔳 2 ， n ܿ ， 在 G 所在圆外， 11. 1 解：连接 AC ‸ 1 2 8 1 与 x 轴交点 㔳 、 㔳 ，点 㔳 ，对称轴 ‸ 1 ， sin ‸ ， 作点 D 关于 y 轴的对称点 h ，作点 A 关于 y 轴的对称点 ，过点 h 作 h 于点 E， 则 h 为所求； 由对称性可知， ‸ ， sin ‸ ， 䁨 ‸ 䁨 ， 再由 h䁨 ‸ h䁨 ， 䁨 䁨h 的最小值为 h ， 㔳 ， h 1㔳 ， h ‸ ， ‸ ， ‸ ， ‸ ， cosh ‸ cos ‸ h ‸ 第 1 页，共 28 页 h ‸ 1 ； 12. 2 㔳 解： 11 ， 11 是 的中位线， 11 ‸ 1 2 ， 11 ． 111 ， 11 ‸ 1 ‸ 1 .同理 1 ‸ 1 ‸ 1 . 1 ‸ 1 1 ‸ 1 2 ； 同理可得， 2 ‸ 2 ； ‸ 2 21 ； 2㔳2㔳 ‸ 2 㔳 ． 13. 1㔳.㔳 12 解：设 ‸ . 2 1㔳.1 2 1㔳.㔳 2 ‸ 2 㔳.㔳 㔳㔳.㔳2 ， ‸ ܿ 㔳 ， 当 ‸ 㔳.㔳 ‸ 1㔳.㔳 时，y 有最小值， 设 ‸ 1 2 2 2 2 ‸ 2 21 2 1 2 2 2 2 ， ܿ 㔳 ， 当 ‸ 212 2 ‸ 12 时，w 有最小值． 第 1 页，共 28 页 14. 或 2 ܿ 1 或 㔳 解：如图所示：把二次函数 ‸ 1 2 2 向左平移 2 个单位得二次函数 ‸ 1 2 2 的图像； 把反比例函数 ‸ 2 向左平移 2 个单位得反比例函数 ‸ 2 2 ， 抛物线 ‸ 1 2 2 和双曲线 ‸ 2 2 的交点为分别是二次函数 ‸ 1 2 2与反比例函数 ‸ 2 的图象的交点向左平移 2 个单位得： 2 、 1 2 和 㔳 1 不等式 1 2 2 2 x2 㔳 得 表示抛物线 ‸ 1 2 2 在 双曲线 ‸ 2 2 的交点或上方， 的解集为： 或 2 ܿ 1 或 㔳 ． 15. 1 2 ； 22 2 1 ， 1 或 ； 㔳 ，且点 B 关于 x 轴的对称点为点 ， 点 㔳 ‸ ‸ ‸ ， 若 h 在 内部，如图，过点 D 作 hn ， 第 18 页，共 28 页 ‸ hn ‸ n ‸ hn ， h ‸ 2hn ， h ܿ 1 ， hn ܿ 2 h ܿ 2 2 点 㔳 ，点 h㔳 ܿ 2 2 ܿ 2 2 若 h 在 外部， h ܿ 1 ， h ܿ 2 点 㔳 ，点 h㔳 ܿ 2 ܿ 综上所述： ܿ ܿ 2 2 解： 1 㔳 ， 㔳 ， 点 A，点 ‸ 㔳 2 㔳 2 ‸ 2 㔳 ， 2㔳 ， 直线 BC 解析式为： ‸ 2 第 1 页，共 28 页 点 A，线段 ‸ 故答案为： 2 ， 2 如图，过点 O 作 于点 E， 㔳 ， 㔳 ， ‸ ‸ ， ‸ 2 ， ‸ 1 2 ‸ 1 2 ‸ 2 2 ，线段 ‸ 2 2 1 ‸ 1 ， 与 各边都不相交， 若 在 外，如图，过点 O 作 n 于点 F， 㔳 ， 2㔳 ， ‸ ， ‸ 2 ‸ 2 2 ‸ 2 ‸ 1 2 ‸ 1 2 n n ‸ ‸ 1 ， n ‸ 1 第 2㔳 页，共 28 页 ‸ 1若 在 内， ‸ 1 ， ‸ 1 ‸ ‸ 故答案为： 1 或 ； 16. 解： 1 图形如图 1 所示． 过点 A 作 t 于点 H， o 交 CB 的延长线于点 G． ， t ， o ， t ‸ to ‸ o ‸ 㔳 ， 四边形 AHCG 是矩形， to ‸ ‸ 㔳 ， t ‸ o ， ‸ ， t≌ o t ‸ o ， 四边形 AHCG 为正方形， h ‸ ． 如图 2 中，延长 GA 交 OD 于点 K． 第 21 页，共 28 页 ‴ ‸ ‸ ， ‸ ， ‸ ， ‸ ， h ‸ ‸ ， h ‸ ． 2 如图 3 中， ‸ ‸ ， ‸ 㔳 ， ‸ 2 ‸ 2 ， 观察图象可知，当 䁨‴ 时， 䁨 是等腰直角三角形，此时 PQ 的值最大，最大 值 ‸ 2䁨 ‸ 1㔳 2 ． 17. 1 证明： 平分钝角 ，BD 平分 ， ‸ 2h ， ‸ 2h ， ‸ 2h h ‸ 2 㔳 ‸ 18㔳 ， ； 第 22 页，共 28 页 2 解： n ‸ 2 2n ；理由如下： h h ‸ 㔳 ， h ， h h ‸ 㔳 ， h ‸ h ， h ‸ h ， ‸ ， 过点 A 作 t 于 H，如图 1 所示： ‸ ， n ， t 、 n 是等腰直角三角形， t ‸ t ‸ tn ， ‸ ‸ 2t ， n ‸ 2 ‸ 2 2t ‸ 2t ， n ‸ n ‸ 2t 2t ‸ 2 2t ， t ‸ n 2 2 ‸ 1 2 2 n ， n ‸ 21 2 2 n ‸ 2 2n ； 当点 F 在点 C 的左侧时，如图 2 所示： 同 得： h ‸ h ， ‸ ‸ 1㔳 ， n ‸ h ， h h ‸ 㔳 ， h n ‸ 㔳 ， n ‸ 㔳 ， n ， 则 ‸ 1 2 n ‸ 1 2 1㔳 n ‸ 㔳 ， n ‸ ， n ‸ 1㔳 2 2 ‸ 8 ， n ‸ n ‸ 1㔳 8 ‸ 2 ， ‸ 2 2 2 ‸ 2 1㔳 ， ‸ 1 2 h ‸ 1 2 2 1㔳 h ‸ 㔳 ， h ‸ 1㔳 ， 作 䁨o 于 G，则 䁨o ‸ 䁨n ， 在 䁨o 和 䁨n 中， h ‸ h ho ‸ hn ， 第 2 页，共 28 页 䁨o≌ 䁨ntሺ ， o ‸ n ‸ 8 ， o ‸ o ‸ 2 ， ‸ ， h ， h ‸ h ‸ 1 2 ‸ 1㔳 ， 设 䁨 ‸ ，则 䁨o ‸ 䁨n ‸ ， 在 䁨o 中，由勾股定理得： 2 2 2 ‸ 2 ， 解得： ‸ 1㔳 ， 䁨 ‸ 1㔳 ， 䁨h ‸ 䁨 2 h 2 ‸ 1㔳 2 1㔳 2 ‸ 1㔳 ， 䁨 ‸ h 䁨h ‸ 1㔳 1㔳 ‸ 8 1㔳 ； 当点 F 在点 C 的右侧时， 则 n ‸ n ， h ， 䁨h ‸ 䁨h ， 䁨 ‸ 䁨 ， 䁨h ‸ 䁨h ‸ 1㔳 ， 䁨 ‸ 8 1㔳 2 1㔳 ‸ 1㔳 1㔳 ； 综上所述，线段 BP 的长为 1㔳 1㔳 或 8 1㔳 ． 18. 1 㔳 ； 2 1㔳 ， 1㔳 ； 第 2 页，共 28 页 连点成线，画出函数图象． 或 1 ； 函数图象在第一、三象限且关于原点对称； ܿ 2 或 ܿ 2. 解： 1 在分母上， 㔳 ． 故答案为： 㔳 ． 2 当 ‸ 1 时， ‸ 1 ‸ 1㔳 ； 当 ‸ 时， ‸ 1 ‸ 1㔳 ． 故答案为： 1㔳 ； 1㔳 ． 见答案． 当 ‸ 1 时，有 1 ‸ 1 ， 解得： 1 ‸ ， 2 ‸ 1 ． 故答案为： 或 1 ． 观察函数图象，可知：函数图象在第一、三象限且关于原点对称． 故答案为：函数图象在第一、三象限且关于原点对称． 1 ‸ 有两个不相等的实数根， 第 2 页，共 28 页 ܿ 2 或 ܿ 2 ． 故答案为： ܿ 2 或 ܿ 2 ． 19. 解： 1 抛物线的顶点为 1 ， 设抛物线的解析式为 ‸ 1 2 ， 将点 㔳 代入抛物线 ‸ 1 2 中，得 ‸ ， ‸ 1 ， 抛物线的解析式为 ‸ 1 2 ‸ 2 2 ； 2 由 1 知，抛物线的解析式为 ‸ 2 2 ， 令 ‸ 㔳 ，则 2 2 ‸ 㔳 ， ‸ 1 或 ‸ ， 㔳 ， 1㔳 ， 令 ‸ 㔳 ，则 ‸ ， 㔳 ， ‸ 1㔳 ， 设点 㔳 ，则 ‸ 2 1 ， ‸ ൌ ൌ ， 是等腰三角形， 当 ‸ 时， 1㔳 ‸ 2 1 ， ‸ 或 ‸ 点 C 的纵坐标，舍去 ， 㔳 ， 当 ‸ 时， 1㔳 ‸ ൌ ൌ ， ‸ 1㔳 ， 㔳 1㔳 或 㔳 1㔳 ， 当 ‸ 时， 2 1 ‸ ൌ ൌ ， ‸ ， 㔳 ， 即满足条件的点 E 的坐标为 㔳 、 㔳 1㔳 、 㔳 1㔳 、 㔳 ； 如图，存在， h1 ， 第 2 页，共 28 页 将线段 BD 向上平移 4 个单位，再向右 或向左 平移适当的距离，使点 B 的对应点落 在抛物线上，这样便存在点 Q，此时点 D 的对应点就是点 P， 点 Q 的纵坐标为 4， 设 ‴ ， 将点 Q 的坐标代入抛物线 ‸ 2 2 中得， 2 2 ‸ ， ‸ 1 2 2 或 ‸ 1 2 2 ， ‴1 2 2 或 1 2 2 ， 分别过点 D，Q 作 x 轴的垂线，垂足分别为 F，G， 抛物线 ‸ 2 2 与 x 轴的右边的交点 B 的坐标为 㔳 ，且 h1 ， n ‸ 䁨o ‸ 1 ‸ 2 ， 点 P 的横坐标为 1 2 2 2 ‸ 1 2 2 或 1 2 2 2 ‸ 1 2 2 ， 即 䁨 1 2 2㔳 、 ‴1 2 2 或 䁨 1 2 2㔳 、 ‴1 2 2 ． 20. 解： 1 抛物线 ‸ 2 ܾ 与 x 轴交于点 A、B 两点，对称轴为直线 ‸ ， 点 A 的坐标为 2㔳 ． 抛物线 ‸ 2 ܾ 过点 2㔳 ， 㔳 ， 㔳 ， 2ܾ ‸ 㔳 ܾ ‸ 㔳 ‸ ， 解得 ‸ 1 2 ， ܾ ‸ ， ‸ ． 抛物线的解析式为： ‸ 1 2 2 ； 2 设 䁨 ， 㔳 ， 㔳 ， 2 ‸ 2 2 ‸ 2 ， 䁨 2 ‸ 2 2 2 ， 䁨 2 ‸ 2 2 ， 当 䁨 ‸ 㔳 时， 2 䁨 2 ‸ 䁨 2 ， 2 2 2 2 ‸ 2 2 ， 解得： ‸ 2 ， 䁨 2 ； 当 䁨 ‸ 㔳 时， 䁨 2 2 ‸ 䁨 2 ， 2 2 2 ‸ 2 2 2 ， 解得： ‸ 1㔳 ， 第 2 页，共 28 页 䁨1㔳 ； 当 䁨 ‸ 㔳 时， 䁨 2 䁨 2 ‸ 2 ． 2 2 2 2 2 ‸ 2 ， 解得： ‸ 1 ． 䁨 1 或 䁨 1.综合以上可得点 P 的坐标为 2 或 1㔳 或 1 或 䁨 1. 过点 Q 作 ‴t 轴于点 H， 㔳 ， 㔳 ， ‸ ， ‸ ， ‸ ， ‴t ‸ t‴ ‸ ， ‴ ‸ 1㔳 2 ， t ‸ ‴t ‸ 1㔳 2 2 2 ‸ 1㔳 ， t ‸ 1㔳 ‸ 8 ， 点 Q 的坐标为 1㔳 8 ， 在 x 轴上取点 o 2㔳 ，连接 QG 交 y 轴于点 M，则此时 ‴ 的周长最小， ‴ ‸ 2 1㔳 2 8 2 ‸ ， ‴o ‸ 1㔳 2 2 8 2 ‸ 8 ， ‴ ‴o ‸ 8 ‸ ， ‴ 的最小周长为 ． 第 28 页，共 28 页