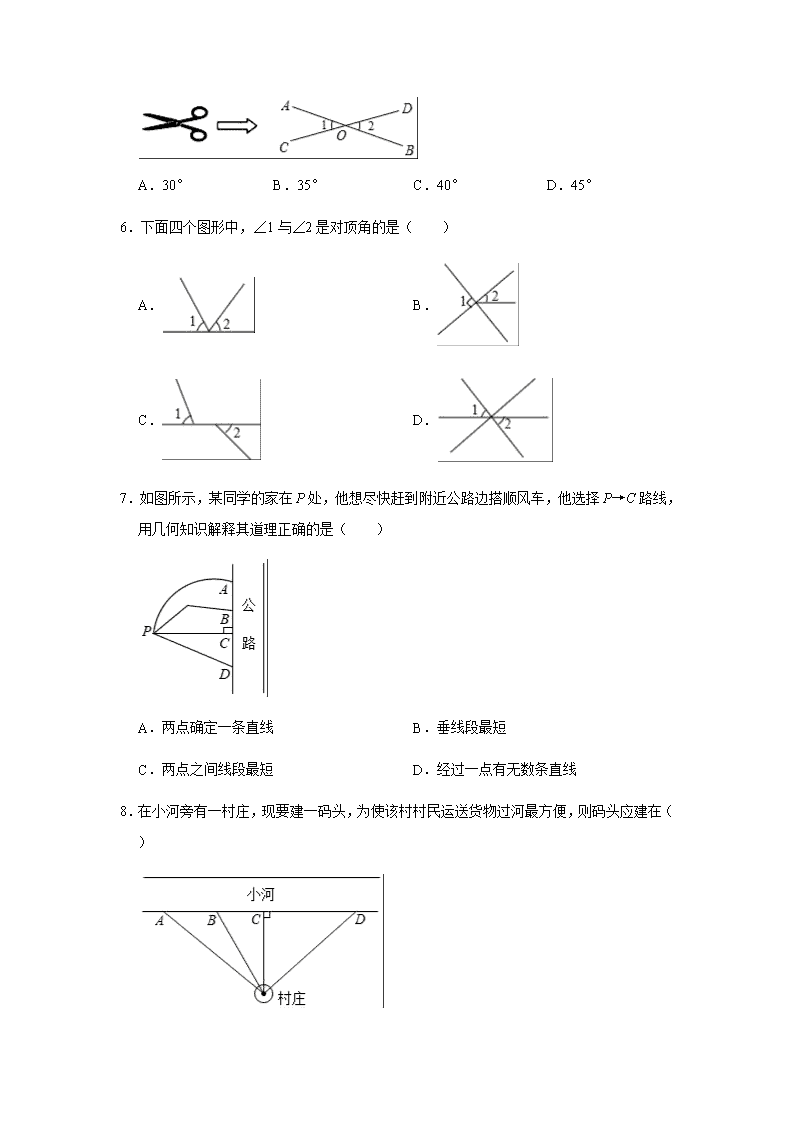人教版数学七年级下册 第5章 5相交线同步测试试题（一） 12页

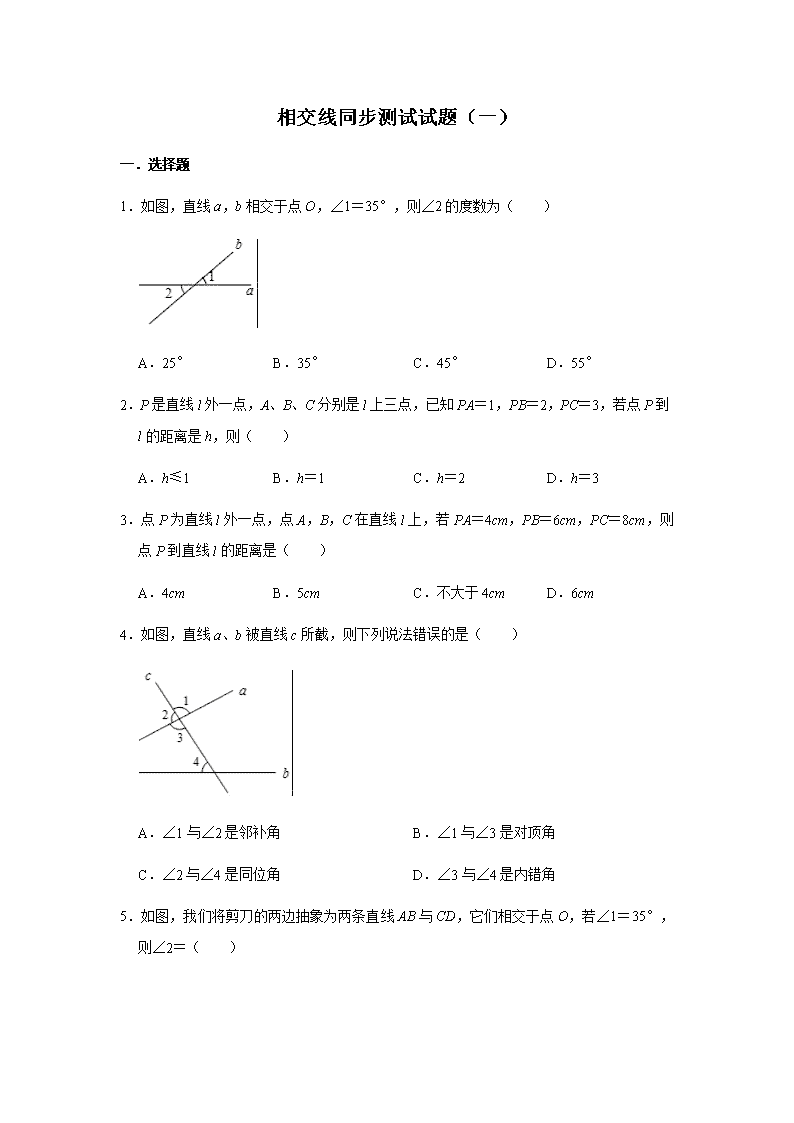
相交线同步测试试题（一） 一．选择题 1．如图，直线 a，b 相交于点 O，∠1＝35°，则∠2 的度数为（ ） A．25° B．35° C．45° D．55° 2．P 是直线 l 外一点，A、B、C 分别是 l 上三点，已知 PA＝1，PB＝2，PC＝3，若点 P 到 l 的距离是 h，则（ ） A．h≤1 B．h＝1 C．h＝2 D．h＝3 3．点 P 为直线 l 外一点，点 A，B，C 在直线 l 上，若 PA＝4cm，PB＝6cm，PC＝8cm，则 点 P 到直线 l 的距离是（ ） A．4cm B．5cm C．不大于 4cm D．6cm 4．如图，直线 a、b 被直线 c 所截，则下列说法错误的是（ ） A．∠1 与∠2 是邻补角 B．∠1 与∠3 是对顶角 C．∠2 与∠4 是同位角 D．∠3 与∠4 是内错角 5．如图，我们将剪刀的两边抽象为两条直线 AB 与 CD，它们相交于点 O，若∠1＝35°， 则∠2＝（ ） A．30° B．35° C．40° D．45° 6．下面四个图形中，∠1 与∠2 是对顶角的是（ ） A． B． C． D． 7．如图所示，某同学的家在 P 处，他想尽快赶到附近公路边搭顺风车，他选择 P→C 路线， 用几何知识解释其道理正确的是（ ） A．两点确定一条直线 B．垂线段最短 C．两点之间线段最短 D．经过一点有无数条直线 8．在小河旁有一村庄，现要建一码头，为使该村村民运送货物过河最方便，则码头应建在 （ ） A．A 点 B．B 点 C．C 点 D．D 点 9．某工程队计划把河水引到水池 A 中，他们先过 A 点作 AB⊥CD，垂足为 B，CD 为河岸， 然后沿 AB 开渠，可以节约人力、物力和财力，这样设计的数学依据是（ ） A．两点之间的所有连线中，线段最短 B．过一点有且只有一条直线垂直于已知直线 C．经过两点有一条直线，并且只有一条直线 D．垂线段最短 10．如图，∠4 的同位角是（ ） A．∠1 B．∠2 C．∠3 D．∠5 二．填空题 11．如图，已知 AO⊥BC 于 O，∠BOD＝120°，那么∠AOD＝ °． 12．如图，∠B 的内错角是 ． 13．如图，点 O 在直线 AB 上，OD⊥OE，垂足为 O，OC 是∠DOB 的平分线，若∠AOD＝ 70°，则∠BOE＝ 度，∠COE＝ 度． 14．如图，直线 AB，CD 相交于点 O，EO⊥AB，垂足为 O，∠AOD＝118°，则∠EOC 的 度数为 ． 15．如图，共有 对同位角，有 对内错角，有 对同旁内角． 三．解答题 16．如图，∠COD 为平角，AO⊥OE，∠AOC＝2∠DOE，求∠AOC． 17．如图，直线 AB、CD 相交于 O，OE⊥CD，且∠BOD 的度数是∠AOD 的 5 倍． 求：（1）∠AOD、∠BOD 的度数； （2）∠BOE 的度数． 18．已知，OM 平分∠AOC，ON 平分∠BOC． （1）如图 1，若 OA⊥OB，∠BOC＝60°，求∠MON 的度数； （2）如图 2，若∠AOB＝80°，∠MON：∠AOC＝2：7，求∠AON 的度数． 19．如图，数轴上点 A，B 表示的数 a，b 满足|a+6|+（b﹣12）2＝0，点 P 为线段 AB 上一点 （不与 A，B 重合），M，N 两点分别从 P，A 同时向数轴正方向移动，点 M 运动速度为 每秒 2 个单位长度，点 N 运动速度为每秒 3 个单位长度，设运动时间为 t 秒（t≠6）． （1）直接写出 a＝ ，b＝ ； （2）若 P 点表示的数是 0． ① t＝1，则 MN 的长为 （直接写出结果）； ② 点 M，N 在移动过程中，线段 BM，MN 之间是否存在某种确定的数量关系，判断并说 明理由； （3）点 M，N 均在线段 AB 上移动，若 MN＝2，且 N 到线段 AB 的中点 Q 的距离为 3， 请求出符合条件的点 P 表示的数． 参考答案与试题解析 一．选择题 1．【解答】解：∵直线 a，b 相交于点 O，∠1＝35°， ∴∠2＝∠1＝35°． 故选：B． 2．【解答】解：∵直线外一点与直线上各点连接的所有线段中，垂线段最短， ∴点 P 到直线 l 的距离 h≤PA，即 h≤1． 故选：A． 3．【解答】解：∵4＜6＜8， ∴根据从直线外一点到这条直线上所有点连线中，垂线段最短， 可知点 P 到直线 l 的距离是 4cm 或比 4cm 小的数， 即不大于 4cm， 故选：C． 4．【解答】解：A、∠1 与∠2 是邻补角，故原题说法正确； B、∠1 与∠3 是对顶角，故原题说法正确； C、∠2 与∠4 是同位角，故原题说法正确； D、∠3 与∠4 是同旁内角，故原题说法错误； 故选：D． 5．【解答】解：∵将剪刀的两边抽象为两条直线 AB 与 CD，它们相交于点 O，∠1＝35°， ∴∠2＝∠1＝35°． 故选：B． 6．【解答】解：A、∠1 与∠2 不是对顶角，故此选项不合题意； B、∠1 与∠2 不是对顶角，故此选项不合题意； C、∠1 与∠2 不是对顶角，故此选项不合题意； D、∠1 与∠2 是对顶角，故此选项符合题意； 故选：D． 7．【解答】解：某同学的家在 P 处，他想尽快赶到附近公路边搭顺风车，他选择 P→C 路线， 是因为垂直线段最短， 故选：B． 8．【解答】解：为使该村村民运送货物过河最方便，则码头应建在 C 处． 故选：C． 9．【解答】解：某工程队计划把河水引到水池 A 中，他们先过 A 点作 AB⊥CD，垂足为 B， 然后沿 AB 开渠，可以节约人力、物力和财力，这样设计的数学依据是：垂线段最短， 故选：D． 10．【解答】解：∠4 的同位角是∠1， 故选：A． 二．填空题（共 5 小题） 11．【解答】解：∵AO⊥BC， ∴∠AOB＝90°， ∵∠BOD＝120°， ∴∠AOD＝∠BOD﹣∠AOB＝120°﹣90°＝30°， 故答案是：30． 12．【解答】解：∠B 的内错角是∠BAD； 故答案为：∠BAD． 13．【解答】解：∵∠BOD＝180°﹣∠AOD＝110°， 又∵OC 是∠DOB 的平分线． ∴∠DOC＝∠COB＝ ∠BOD＝55°， ∵OD⊥OE，垂足为 O． ∴∠COE＝90°﹣∠DOC＝90°﹣55°＝35°， ∠BOE＝∠COB﹣∠COE＝55°﹣35°＝20°． 故答案是：20 和 35． 14．【解答】解：∵∠AOD＝118°， ∴∠BOC＝∠AOD＝118°， ∵EO⊥AB ， ∴∠BOE＝90°， ∴∠EOC＝∠BOC﹣∠BOE＝28°， 故答案为：28°． 15．【解答】解：同位角：∠AEO 和∠CGE，∠OEF 和∠EGH，∠OFB 和∠OHD，∠OFE 和∠OHG，∠IGH 和∠IEF，∠AEI 和∠CGI，∠AFJ 和∠CHJ，∠DHJ 和∠JFB，∠AEO 和∠AFO，∠OEB 和∠OFB，∠AEG 和∠AFH，∠GEB 和∠HFB，∠EGH 和∠OHD， ∠OGC 和∠OHC，∠O 与∠EFH，∠O 与∠GEF，∠O 和∠IGH，∠O 和∠GHJ， ∠CGI 和∠CHJ，∠HGI 和∠DHJ，共 20 对； 内错角：∠O 和∠OEA，∠O 和∠OFB，∠O 和∠OGC，∠O 和∠OHD，∠AEG 和∠EGH， ∠BEG 和∠EGC，∠BFH 和∠FHC，∠AFH 和∠FHD，∠OEF 和∠EFH，∠GEF 和∠ OFE，∠OGH 和∠GHJ，∠OHG 和∠IGH，共 12 对； 同旁内角：∠OEF 和∠O，∠OFE 和∠O，∠O 和∠OGH，∠O 和∠OHC，∠OEF 和∠ OFE，∠OGH 和∠OHG，∠GEF 和∠EFH，∠IGH 和∠GHJ，∠AEG 和∠CGE，∠BFH 和∠FHD，∠FEG 和∠EGH，∠EFH 和∠GHF，共 12 对， 故答案为：20；12；12． 三．解答题（共 4 小题） 16．【解答】解：∵∠COD 为平角，AO⊥OE， ∴∠AOC+∠DOE＝∠COD﹣∠AOE＝180°﹣90°＝90°． 又∵∠AOC＝2∠DOE， ∴∠AOC＝ ×90°＝60°． 17．【解答】解：（1）∵AB 是直线（已知）， ∴∠BOD+∠AOD＝180°， ∵∠BOD 的度数是∠AOD 的 5 倍， ∴∠AOD＝ ×180°＝30°，∠BOD＝ ×180°＝150°． （2）∵∠BOC＝∠AOD＝30°，OE⊥DC， ∴∠EOC＝90°， ∴∠BOE＝∠EOC﹣∠BOC＝90°﹣30°＝60°． 18．【解答】解：（1）∵OA⊥OB， ∴∠AOB＝90°， ∵∠AOC＝∠AOB+∠BOC，∠BOC＝60°， ∴∠AOC＝90°+60°＝150°， ∵OM 平分∠AOC， ∴∠COM＝ ∠AOC＝75°， ∵ON 平分∠BOC， ∴∠CON＝ ∠BOC＝ ×60°＝30°， ∴∠MON＝∠COM﹣∠CON＝75°﹣30°＝45°； （2）∵∠COM＝ ∠AOC，∠CON＝ ∠BOC， ∴∠MON＝ （∠AOC﹣∠BOC）＝ ∠AOB＝40°， ∵∠MON：∠AOC＝2：7， ∴∠AOC＝140°， ∵OM 平分∠AOC， ∴∠AOM＝ ∠AOC＝70°， ∴∠AON＝∠AOM+∠MON＝70°+40°＝110° 19．【解答】解：（1）∵|a+6|+（b﹣12）2＝0， ∴a+6＝0，b﹣12＝0， ∴a＝﹣6，b＝12； 故答案为：﹣6，12； （2） ① 2﹣[（﹣6）+3]＝5， 故答案为：5； ② BM＝2MN， 理由：由题意得，PM＝2t，AN＝3t， 当点 N 在 M 的左边时，如图 1， ∴BM＝12﹣2t，MN＝AB﹣AN﹣BM＝18﹣3t﹣（12﹣2t）＝6﹣t， ∴BM＝2MN； 当 N 在 M 的右边，如图 2， ∴BM＝2t﹣12，MN＝AN﹣AP﹣PM＝3t﹣6﹣（2t﹣12）＝t﹣6， ∴BM＝2MN； 综上所述，点 M，N 在移动过程中，BM＝2MN； （3）设点 P 表示的数为 x，点 N 表示的数为﹣6+3t， 根据题意得，|（x+2t）﹣（﹣6+3t）|＝2， 解得：x﹣t＝﹣4 或 x﹣t＝﹣8， ∵Q 为线段 AB 的中点，Q 表示的数为 3， 即 QN＝3，点 N 表示的数为 0 或 6， ∴﹣6+3t＝0 或﹣6+3t＝6，解得：t＝2 或 4， ① 当 t＝2 时，由 x﹣t＝﹣4 得，x＝﹣2，由 x﹣t＝﹣8 得，x＝﹣6（P 此时与点 A 重合， 不符合题意，舍去）， ② 当 t＝4 时，由 x﹣t＝﹣4 得，x＝0，由 x﹣t＝﹣8 得，x＝﹣4， 综上所述，符合条件的点 P 表示的数为﹣2，0 或﹣4．