八年级下册数学同步练习2-5-2 矩形的判定1 湘教版 6页

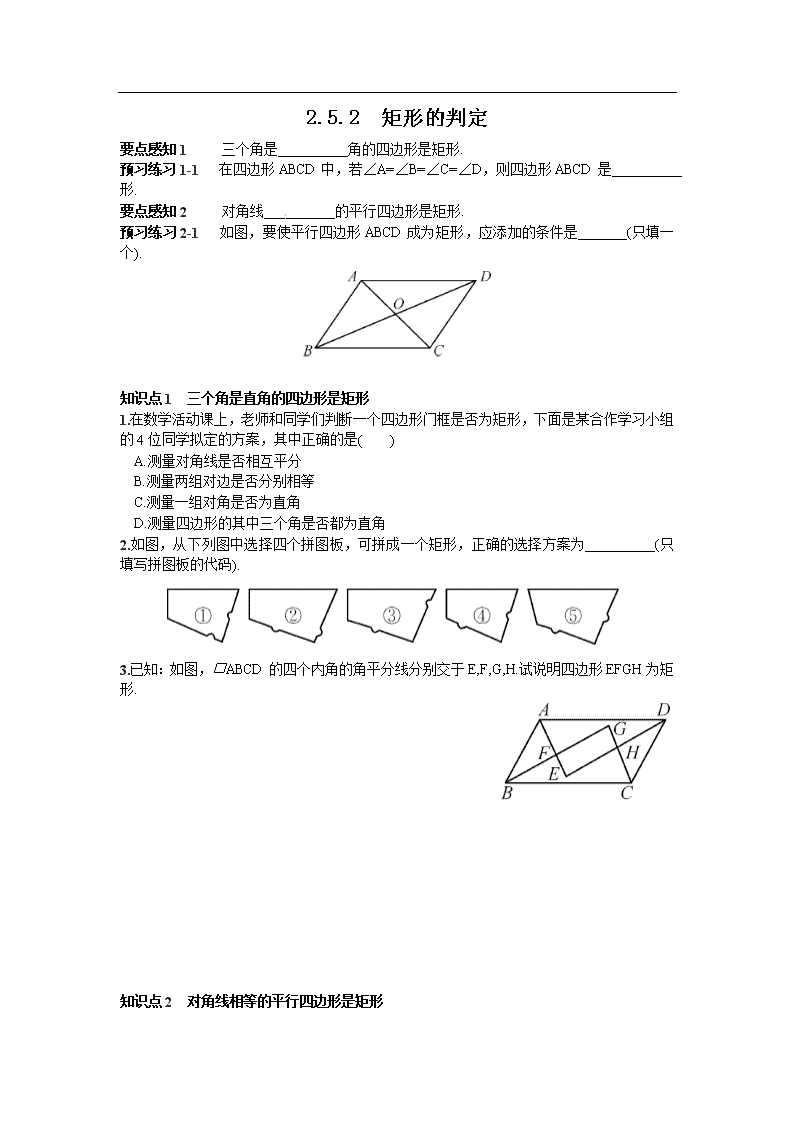
‎2.5.2 矩形的判定 要点感知1 三个角是__________角的四边形是矩形.‎ 预习练习1-1 在四边形ABCD中，若∠A=∠B=∠C=∠D，则四边形ABCD是__________形.‎ 要点感知2 对角线__________的平行四边形是矩形.‎ 预习练习2-1 如图，要使平行四边形ABCD成为矩形，应添加的条件是_______(只填一个).‎ 知识点1 三个角是直角的四边形是矩形 ‎1.在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是某合作学习小组的4位同学拟定的方案，其中正确的是( )‎ ‎ A.测量对角线是否相互平分 ‎ B.测量两组对边是否分别相等 ‎ C.测量一组对角是否为直角 ‎ D.测量四边形的其中三个角是否都为直角 ‎2.如图，从下列图中选择四个拼图板，可拼成一个矩形，正确的选择方案为__________(只填写拼图板的代码).‎ ‎[来源:学科网]‎ ‎3.已知：如图，□ABCD的四个内角的角平分线分别交于E,F,G,H.试说明四边形EFGH为矩形.‎ 知识点2 对角线相等的平行四边形是矩形 ‎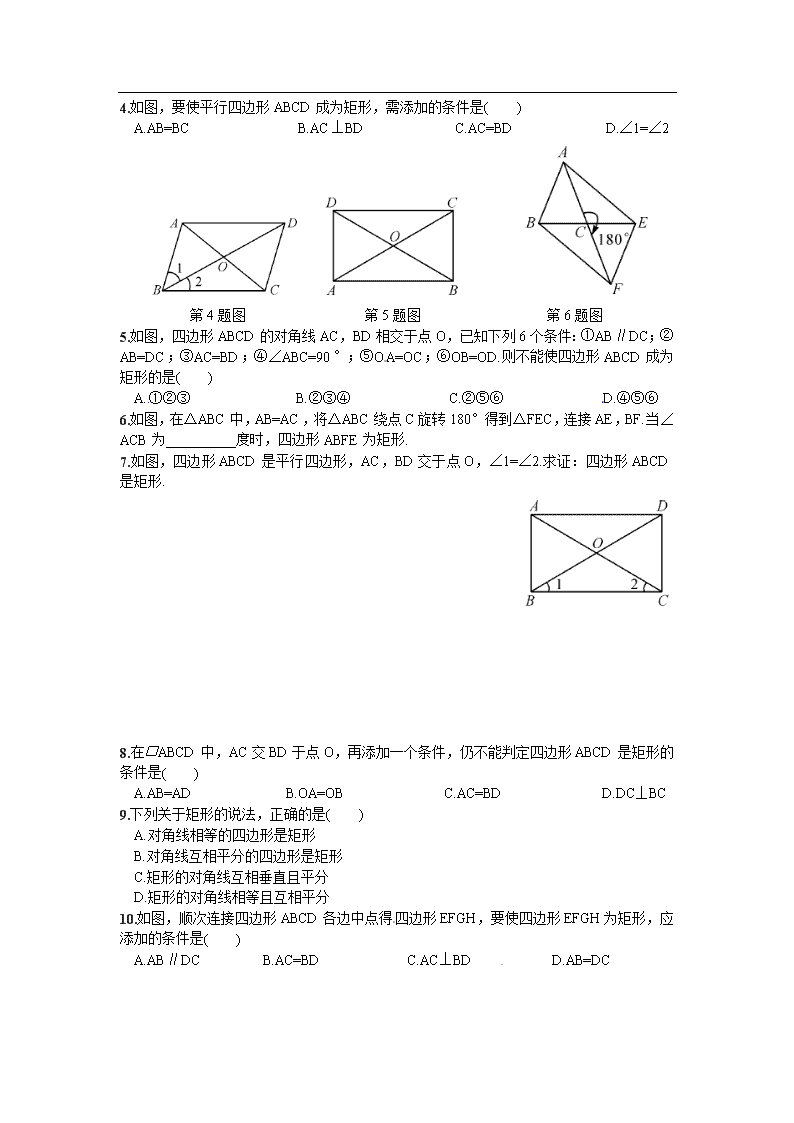4.如图，要使平行四边形ABCD成为矩形，需添加的条件是( )‎ ‎ A.AB=BC B.AC⊥BD C.AC=BD D.∠1=∠2‎ ‎ ‎ 第4题图 第5题图 第6题图 ‎5.如图，四边形ABCD的对角线AC，BD相交于点O，已知下列6个条件：①AB∥DC；②AB=DC；③AC=BD；④∠ABC=90°；⑤OA=OC；⑥OB=OD.则不能使四边形ABCD成为矩形的是( )‎ ‎ A.①②③ B.②③④ C.②⑤⑥ D.④⑤⑥‎ ‎6.如图，在△ABC中，AB=AC，将△ABC绕点C旋转180°得到△FEC，连接AE，BF.当∠ACB为__________度时，四边形ABFE为矩形.‎ ‎7.如图，四边形ABCD是平行四边形，AC，BD交于点O，∠1=∠2.求证：四边形ABCD是矩形.‎ ‎8.在□ABCD中，AC交BD于点O，再添加一个条件，仍不能判定四边形ABCD是矩形的条件是( )‎ ‎ A.AB=AD B.OA=OB C.AC=BD D.DC⊥BC ‎9.下列关于矩形的说法，正确的是( )‎ ‎ A.对角线相等的四边形是矩形 ‎ B.对角线互相平分的四边形是矩形 ‎ C.矩形的对角线互相垂直且平分 ‎ D.矩形的对角线相等且互相平分 ‎10.如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，应添加的条件是( )‎ ‎ A.AB∥DC B.AC=BD C.AC⊥BD D.AB=DC ‎ ‎ 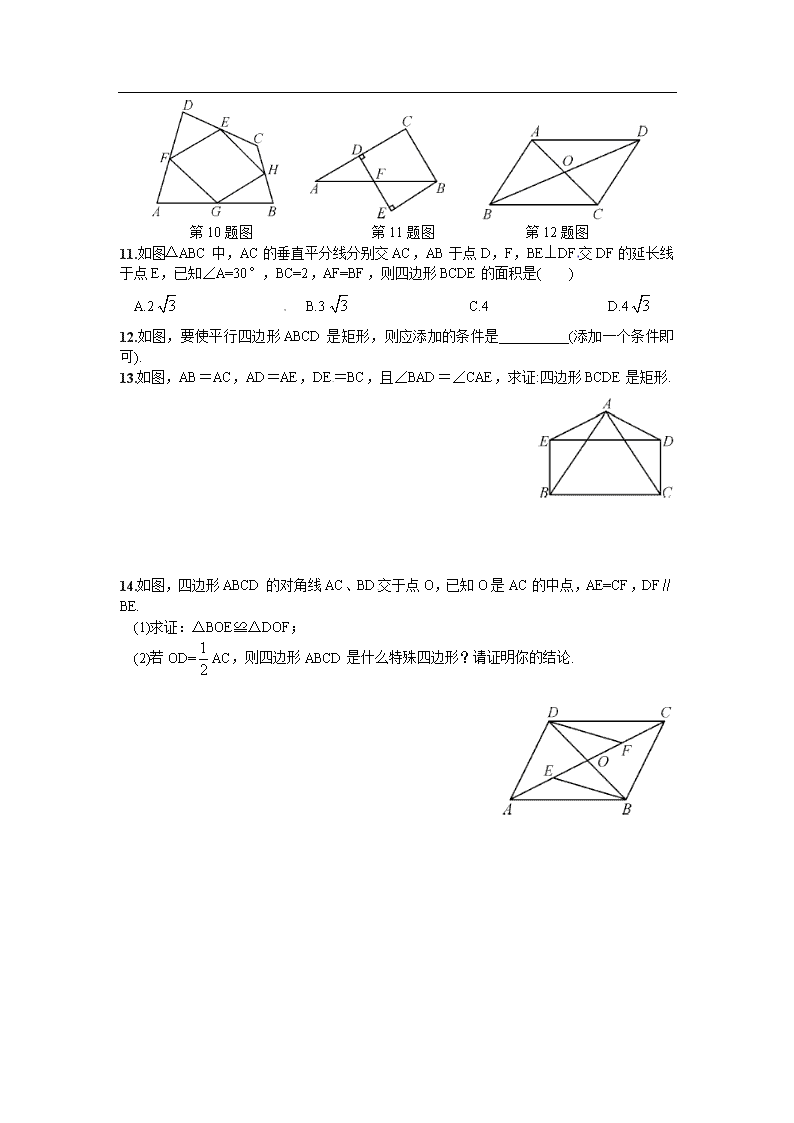第10题图 第11题图 第12题图 ‎11.如图△ABC中，AC的垂直平分线分别交AC，AB于点D，F，BE⊥DF交DF的延长线于点E，已知∠A=30°，BC=2，AF=BF，则四边形BCDE的面积是( )‎ ‎ A.2 B.3 C.4 D.4‎ ‎12.如图，要使平行四边形ABCD是矩形，则应添加的条件是__________(添加一个条件即可).‎ ‎13.如图，AB＝AC，AD＝AE，DE＝BC，且∠BAD＝∠CAE，求证:四边形BCDE是矩形.‎ ‎[来源:学|科|网]‎ ‎14.如图，四边形ABCD的对角线AC、BD交于点O，已知O是AC的中点，AE=CF，DF∥BE.‎ ‎ (1)求证：△BOE≌△DOF；[来源:学_科_网Z_X_X_K]‎ ‎ (2)若OD=AC，则四边形ABCD是什么特殊四边形？请证明你的结论.‎ ‎15.如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC.设MN交∠ACB的角平分线于点E，交∠ACB的外角角平分线于点F.‎ ‎ (1)求证：OE=OF；‎ ‎ (2)若CE＝12，CF＝5，求OC的长；‎ ‎ (3)当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由.‎ ‎[来源:Zxxk.Com]‎ 参考答案 ‎ ‎ ‎ ‎ 要点感知1 直 预习练习1-1 矩 要点感知2 相等 预习练习2-1 答案不唯一，如∠BAD=90°或AC=BD等 ‎1.D 2.①②③④‎ ‎3.∵四边形ABCD是平行四边形，‎ ‎ ∴BC∥AD，AB∥CD.‎ ‎ ∴∠ABC+∠BCD=180°，∠BAD+∠ABC=180°.‎ ‎ 又□ABCD的四个内角的角平分线分别交于E,F,G,H.‎ ‎ ∴∠BAF+∠ABF=90°，∠GBC+∠GCB=90°.‎ ‎ ∴∠GFE=∠AFB=90°，∠G=90°.‎ ‎ 同理可证∠GHE=90°，∠E=90°.‎ ‎ ∴四边形EFGH为矩形.‎ ‎4.C 5.C 6.60‎ ‎7.证明：∵∠1=∠2，‎ ‎∴BO=CO，即2BO=2CO.‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AO=CO，BO=OD.‎ ‎∴AC=2CO，BD=2BO.‎ ‎∴AC=BD.‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴四边形ABCD是矩形.‎ ‎8.A 9.D 10.C 11.A 12.答案不唯一，如：∠ABC=90°或AC=BD ‎13.证明：∵AC＝AB，AD＝AE，∠BAD＝∠CAE，‎ ‎∴∠BAD-∠CAB＝∠CAE-∠CAB，即∠CAD=∠BAE.‎ ‎∴△ADC≌△AEB（SAS）.‎ ‎∴DC＝BE.‎ 又∵DE＝BC，‎ ‎∴四边形BCDE是平行四边形.‎ 连接BD，CE.‎ ‎∵AB＝AC，AD＝AE，∠BAD＝∠CAE，‎ ‎∴△ABD≌△ACE(SAS).‎ ‎∴BD＝CE.‎ ‎∴四边形BCDE是矩形.‎ ‎14.(1)证明：∵O是AC的中点，∴OA=OC.‎ ‎∵AE=CF，∴OE=OF.‎ ‎∵DF∥BE，∴∠OEB=∠OFD.‎ 又∵∠EOB=∠FOD，‎ ‎∴△BOE≌△DOF.‎ ‎ (2)∵△BOE≌△DOF，∴OD=OB.‎ ‎∵OA=OC，‎ ‎∴四边形ABCD是平行四边形.‎ ‎∵OD=AC，OD=BD，‎ ‎∴AC=BD，‎ ‎∴四边形ABCD是矩形.‎ ‎15.(1)证明：∵CF平分∠ACD，且MN∥BD，‎ ‎∴∠ACF=∠FCD=∠CFO.‎ ‎∴OF=OC，‎ 同理可证：OC=OE，‎ ‎∴OE=OF.‎ ‎ (2)由(1)知：OF=OC，OC=OE，‎ ‎∴∠OCF=∠OFC，∠OCE=∠OEC.‎ ‎∴∠OCF+∠OCE=∠OFC+∠OEC，[来源:学科网]‎ 而∠OCF+∠OCE+∠OFC+∠OEC=180°，‎ ‎∴∠ECF=∠OCF+∠OCE=90°，‎ ‎∴EF===13.‎ ‎∴OC=EF=.‎ ‎ (3)当点O移动到AC中点时，四边形AECF为矩形.‎ ‎ 理由：由(1)知OE=OF，当点O移动到AC中点时有OA=OC，‎ ‎∴四边形AECF为平行四边形.‎ 又∵∠ECF=90°，‎ ‎∴四边形AECF为矩形.‎