2020八年级数学上册 第13章 轴对称复习学案（无答案）（新版）新人教版 9页

课题：第13章 轴对称复习 ‎ ‎【学习目标】1、加深认识轴对称、轴对称图形，轴对称的基本性质，加深理解对应点连线被对称轴垂直平分的性质。‎ ‎2、加深理解线段的垂直平分线的概念并掌握其性质；理解等腰三角形、等边三角形的有关概念，并掌握它们的性质及判定方法。‎ ‎【学习过程】一、自主复习，盘点知识（一）基本概念 ‎1.轴对称图形：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做 ，这条直线就叫做 。折叠后重合的点是对应点，叫做 。‎ ‎2.轴对称：把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线 ，这条直线叫做 ，折叠后重合的点是对应点，叫做 。（说明：两个图形关于某条直线对称也叫两个图形成轴对称）。‎ ‎3.线段的垂直平分线：经过线段 点并且 这条线段的直线，叫做该线段的垂直平分线。‎ ‎4.等腰三角形:有 的三角形，叫做等腰三角形。相等的两条边叫做 ，另一条边叫做 ，两腰所夹的角叫做 ，底边与腰的夹角叫做 。‎ ‎5.等边三角形: 三条边都 的三角形叫做等边三角形。‎ ‎（二）主要性质 ‎1.如果两个图形关于某条直线对称，那么对称轴是任何一对对应称点所连线段的 。轴对称图形的对称轴，是任何一对对称点所连线段的 。‎ ‎2.线段垂直平分钱的性质：线段垂直平分线上的点与这条线段两个端点的距离 。‎ ‎3.通过画出坐标系上的两组对称点观察得出：‎ ‎（1）点P（x，y）关于x轴对称的点的坐标为P′（ ， ）。‎ ‎（2）点P（x，y）关于y轴对称的点的坐标为P″（ ， ）。‎ ‎4.等腰三角形的性质：‎ ‎（1）等腰三角形的两个底角 （简称“等边对等角” ）。‎ ‎（2）等腰三角形的顶角 、底边上的 、底边上的 相互重合。‎ ‎（3）等腰三角形是轴对称图形，底边上的中线（顶角平分线、底边上的高）所在直线就是它的 。‎ ‎（4）等腰三角形两腰上的高、中线分别 ，两底角的平分线也 。‎ ‎5.等边三角形的性质 ‎（1）等边三角形的三个内角都 ，并且每一个角都等于 。‎ - 9 -‎ ‎（2）等边三角形是轴对称图形，共有 条对称轴。‎ ‎（3）等边三角形每边上的 、 和该边所对内角的 互相重合。‎ ‎6.在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的 。‎ ‎（三）有关判定 ‎1.与一条线段两个端点距离 的点，在这条线段的垂直平分线上。‎ ‎2.如果一个三角形有两个角 ，那么这两个角所对的边也 （简写成“等角对等边”）。‎ ‎3.三个角都相等的三角形是 三角形。‎ ‎4.有一个角是60°的 是等边三角形。‎ 二、基础训练 ‎1．下列各时刻是轴对称图形的为（ ）．‎ ‎ A、 B、 C、 D、‎ ‎2．小明从镜子里看到镜子对面电子钟的像如图所示，实际时间是（ ）．‎ A、21：10 B、10：‎21 C、10：51 D、12：01 ‎ ‎3．如图是屋架设计图的一部分，其中∠A=30°，点D是斜梁AB的中点，BC、DE垂直于横梁AC，AB=‎16m，则DE的长为（ ）．‎ A、‎8 m B、‎4 m C、‎2 m D、‎‎6 m 4． 等腰三角形是轴对称图形，其对称轴是_______________________________．‎ ‎2、一个汽车车牌在水中的倒影为，则该车的牌照号码是　　　　　　．‎ 5． ‎5.已知点A（x， －4）与点B（3，y）关于x轴对称，那么x＋y的值为____________.‎ ‎6．等腰三角形一腰上的高与另一腰上的夹角为30°，则顶角的度数为 __ ．‎ ‎7.如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为‎12cm2，则图中阴影部分的面积是 ___ cm2. 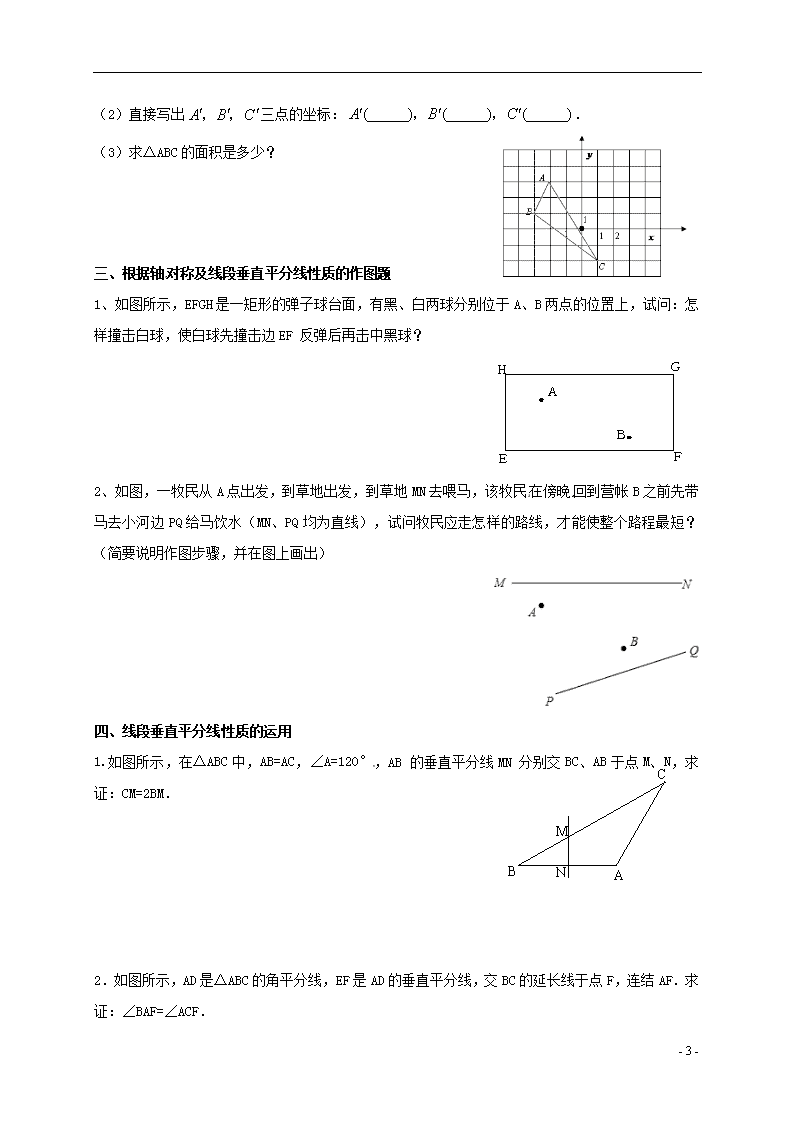‎ ‎8、（1）请画出关于轴对称的（其中分别是的对应点，不写画法）；‎ - 9 -‎ ‎（2）直接写出三点的坐标：． ‎ ‎（3）求△ABC的面积是多少？‎ 三、根据轴对称及线段垂直平分线性质的作图题 ‎1、如图所示，EFGH是一矩形的弹子球台面，有黑、白两球分别位于A、B两点的位置上，试问：怎样撞击白球，使白球先撞击边EF反弹后再击中黑球？‎ ‎2、如图，一牧民从A点出发，到草地出发，到草地MN去喂马，该牧民在傍晚回到营帐B之前先带马去小河边PQ给马饮水（MN、PQ均为直线），试问牧民应走怎样的路线，才能使整个路程最短？（简要说明作图步骤，并在图上画出）‎ 四、线段垂直平分线性质的运用 N M C B A ‎1.如图所示，在△ABC中，AB=AC，∠A=120°，AB的垂直平分线MN分别交BC、AB于点M、N，求证：CM=2BM．‎ ‎2．如图所示，AD是△ABC的角平分线，EF是AD的垂直平分线，交BC的延长线于点F，连结AF．求证：∠BAF=∠ACF．‎ - 9 -‎ 五、等腰三角形边与角计算中的分类讨论思想与方程思想 ‎1、已知等腰三角形的一个内角是800，则它的另外两个内角是 ；‎ ‎2、已知等腰三角形的一个内角是1000，则它的另外两个内角是 ；‎ ‎3、已知等腰三角形有两边的长分别为6，3，则这个等腰三角形的周长是 ；‎ ‎4、已知等腰三角形的周长为24，一边长为6，则另外两边的长是 ；‎ ‎5、已知等腰三角形的周长为24，一边长为10，则另外两边的长是 ；‎ ‎6、等腰三角形的周长是16，其中两边之差为2，则它的三边的长分别为 ；‎ ‎7、等腰三角形一腰上的高与另一腰的夹角为30°，则它的顶角度数为 ；‎ ‎8、一等腰三角形一腰上的中线把这个三角形的周长分成‎15cm和‎18cm两部分，则这个等腰三角形的底边长是 ；‎ ‎9、如图， ∠DEF =36°，AB=BC=CD=DE=EF，求∠A的度数。‎ F E D C B A 六、关于等腰三角形证明题 1、 如图所示，F、C是线段BE上的两点， A、D分别在线段QC、RF上， AB=DE，BF=CE，∠B=∠E，QR∥BE．求证：△PQR是等腰三角形．‎ P Q R F E D C B A - 9 -‎ ‎2、如图，在Rt△ABC中，AB=AC，∠BAC=90°，D为 BC的中点.‎ ‎（1）写出点D到ΔABC三个顶点 A、B、C的距离的关系（不要求证明）‎ ‎（2）如果点M、N分别在线段AB、AC上移动， 在移动中保持AN=BM，请判断△DMN的形状，并证明你的结论 N M D C B A 课题：第13章 轴对称复习 ‎ ‎【学习目标】‎ ‎1、回顾本章知识，形成本章知识结构，总结解题规律。‎ ‎2、培养良好的观察、操作、想象、推理能力 一、选择题（本大题共10题，每小题3分，共30分）‎ ‎1、下列说法正确的是（ ）．‎ A．轴对称涉及两个图形，轴对称图形涉及一个图形 B．如果两条线段互相垂直平分，那么这两条线段互为对称轴 C．所有直角三角形都不是轴对称图形 D．有两个内角相等的三角形不是轴对称图形 ‎2、点M（1，2）关于轴对称的点的坐标为（ ）．‎ A．（－1，－2） B．（－1，2） C．（1，－2） D．（2，－1）‎ ‎3、下列图形中对称轴最多的是( ) ．‎ A．等腰三角形 B．正方形 C．圆 D．线段 ‎4、已知直角三角形中30°角所对的直角边为2，则斜边的长为（ ）．‎ A．2 B．‎4‎ C．6 D．8‎ ‎5、若等腰三角形的周长为26，一边为11，则腰长为（ ）．‎ A．11 B．‎7.5‎ C．11或7.5 D．以上都不对 - 9 -‎ ‎6、如图所示，是四边形ABCD的对称轴，AD∥BC，现给出下列结论：‎ ‎①AB∥CD；②AB=BC；③AB⊥BC；④AO=OC 其中正确的结论有（ ）．‎ A．1个 B．2个 C．3个 D．4个 ‎7、如图：DE是△ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则△EBC的周长为（ ）厘米．‎ A．16 B．‎18 C．26 D．28‎ ‎8、小明从镜子里看到镜子对面电子钟的像如图所示，实际时间是（ ）．‎ ‎︰‎ A、21：10 B、10：21 ‎ C、10：51 D、12：01‎ ‎9、若等腰三角形腰上的高是腰长的一半，则这个等腰三角形的底角是 （ ）．‎ A．75°或15° B．75° C．15° D．75°和30°‎ ‎ 10、等腰三角形ABC在直角坐标系中，底边的两端点坐标是(-2，0)，(6，0)，则其顶点的坐标，能确定的是（ ）．‎ A．横坐标 B．纵坐标 C．横坐标及纵坐标 D．横坐标或纵坐标 二、填空题（每小题3分，共30分）‎ ‎11、已知点P在线段AB的垂直平分线上，PA=6，则PB= ．‎ ‎12、等腰三角形一个底角是30°，则它的顶角是__________度．‎ ‎13、等腰三角形的一内角等于50°，则其它两个内角各为 ．‎ ‎14.如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为‎12cm2，则图中阴影部分的面积是 ___ cm2. ‎ B A C D F E A B D C 第14题图 第15题图 第16题图 第17题图 ‎15．如图,在△ABC中, AB=AC, D为BC上一点,且,AB=BD,AD=DC,则∠C= ____ 度..‎ ‎16．如图，在等边中，分别是上的点，且，则 度．‎ - 9 -‎ ‎17．如图：在△ABC中，AB=AC=9，∠BAC=120°，AD是△ABC的中线，AE是∠BAD的角平分线，DF∥AB交AE的延长线于点F，则DF的长为 ；‎ ‎18.已知点A（x， －4）与点B（3，y）关于x轴对称，那么x＋y的值为____________.‎ ‎19．如果一个三角形是轴对称图形，且有一个角是60°，那么这个三角形是________三角形．‎ ‎20．已知A（-1，-2）和B（1，3），将点A向______平移________ 个单位长度后得到的点与点B关于轴对称．‎ 三、解答题：‎ B ‎ C ‎ A ‎ ‎21、已知：如图，已知△ABC，分别画出与△ABC关于轴对称的图形△A1B‎1C1 和△A2B‎2C2 ；（4分）‎ ‎22、作图题（保留作图痕迹）‎ ‎（1）作线段AB的中垂线EF（4分）‎ ‎（2）作∠AOB的角平分线OC（4分）‎ ‎（3）在公路MN上修一个车站P，使得P向A，B两个地方的距离和最小，请在图中画出P的位置。（4分）‎ ‎ ‎ - 9 -‎ ‎23.如图，AC和BD相交于点O，且AB//DC，OC=OD，求证：OA=OB。（6分）‎ ‎24.如图，点D、E在△ABC的边BC上，AD=AE，AB=AC，求证：BD=EC。（6分）‎ ‎25．（6分）在△ABC中，AB＝AC，AD⊥BC，∠BAD＝40°，AD＝AE．求∠CDE的度数．‎ - 9 -‎ A B P C 北 ‎26、（6分）如图，一艘轮船从点A向正北方向航行，每小时航行15海里，小岛P在轮船的北偏西15°，3小时后轮船航行到点B，小岛P此时在轮船的北偏西30°方向，在小岛P的周围20海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由。‎ - 9 -‎