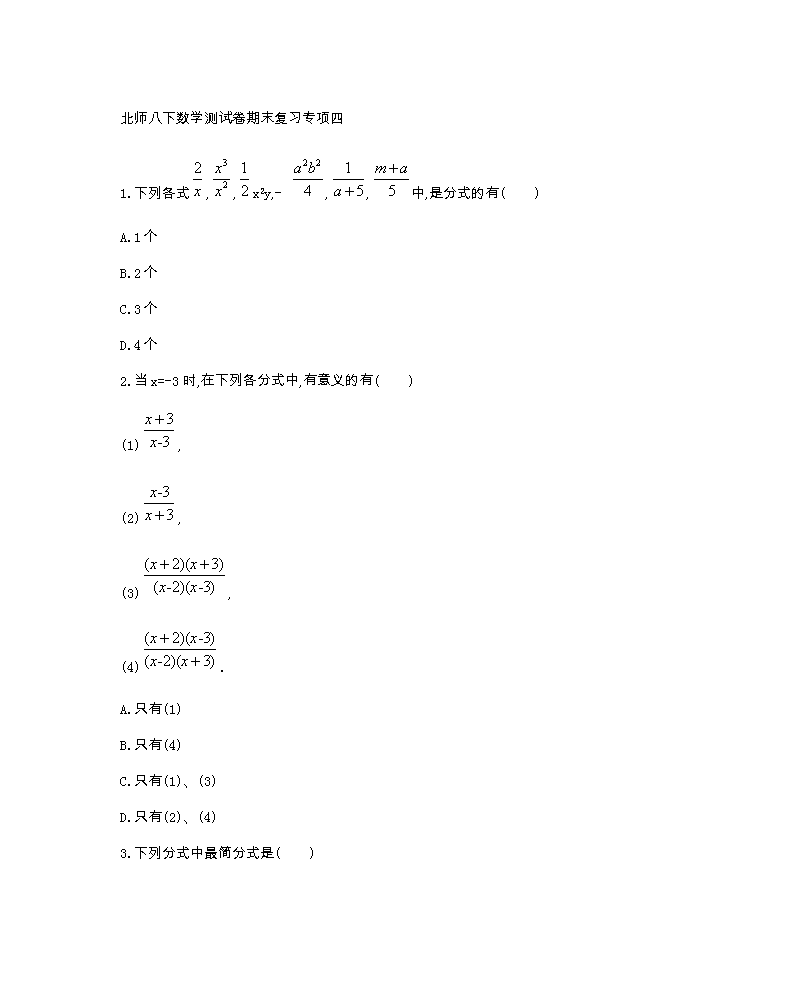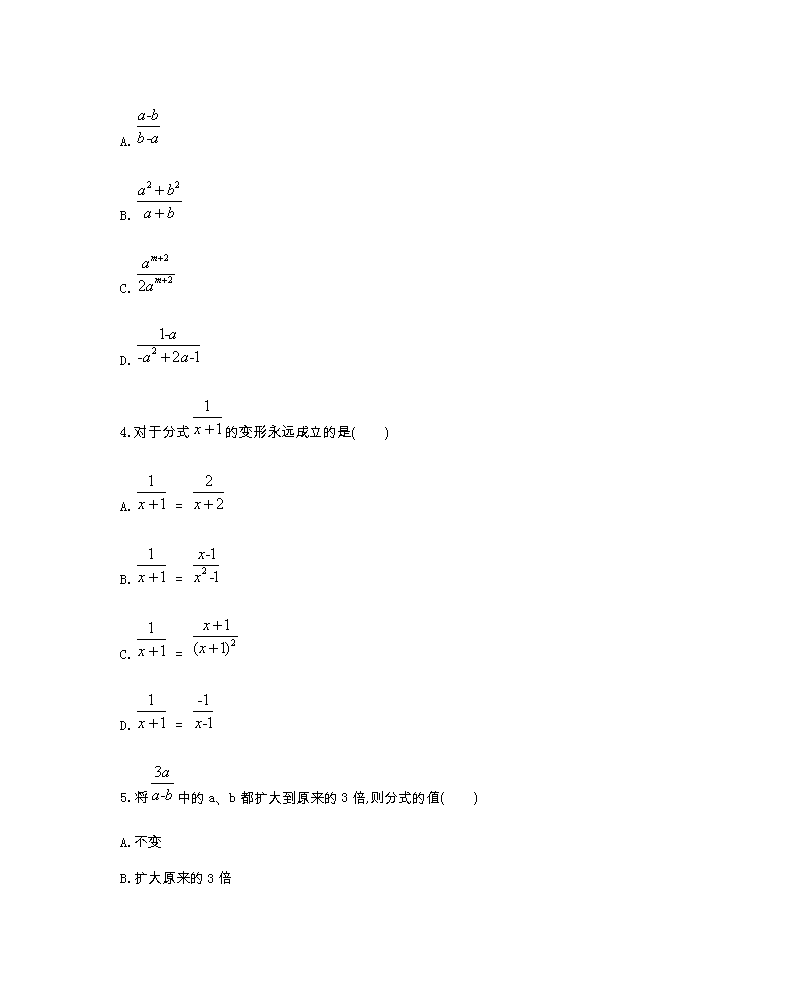- 218.24 KB
- 2021-11-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
北师八下数学测试卷期末复习专项四
1.下列各式,,x2y,- ,,中,是分式的有( )
A.1个
B.2个
C.3个
D.4个
2.当x=-3时,在下列各分式中,有意义的有( )
(1),
(2),
(3),
(4).
A.只有(1)
B.只有(4)
C.只有(1)、(3)
D.只有(2)、(4)
3.下列分式中最简分式是( )
A.
B.
C.
D.
4.对于分式的变形永远成立的是( )
A. =
B. =
C. =
D. =
5.将中的a、b都扩大到原来的3倍,则分式的值( )
A.不变
B.扩大原来的3倍
C.扩大原来的9倍
D.扩大原来的6倍
6.计算:( - ) × =( )
A.a+12
B.2a-12
C.a-12
D.2a+12
7.如果m>n,则下列各式一定不成立的是( )
A.5+m>5+n
B.5m>5n
C.5-m>5-n
D.
8.分式方程 = 的解为( )
A.x=-1
B.x=1
C.x=-3
D.x=3
9.当x 时,有意义.
10.物理学中,并联电路中总电阻R和各支路电阻R1、R2满足关系 = + ,若R1=10,R2=15,总电阻R= .
11.若关于x的分式方程 -2=无解,则m的值为 .
12.写出一个分母至少含有两项且能够约分的分式 .
13.桶中装有液状纯农药a升,刚好一满桶,第一次倒出8升后用水加满,第二次又倒出混合药4升,则这4升混合药液中的含药量为 升.
14.大拖拉机m天耕地a公顷,小拖拉机n天耕地b公顷,大拖机的工作效率是小拖机的工作效率的 倍.
15.计算下列各式.
(1)a2 ÷ b ÷ ÷ c × ÷ d ×
(2) - x-1
(3)( - ) ÷
16.解下列分式方程.
(1) - =
(2) + =1.
17.若方程=-1的解是正数,求a的取值范围.
关于这道题,有位同学作出如下解答:
解:去分母得,2x+a=-x+2.
化简,得3x=2-a.
故x=.
欲使方程的根为正数,必须>0,得a<2.
所以,当a<2时,方程=-1的解是正数.
上述解法是否有误?若有错误请说明错误的原因,并写出正确解答;若没有错误,请说出每一步解法的依据.
18.进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话:
通过这段对话,请你求出该地驻军原来每天加固的长度.
19.甲、乙两工程队共同完成一项工程,乙队先单独做1天后,再由两队合作两天就完成了全部工程,已知甲队单独完成工程所需的天数是乙队单独完成所需天数的,求甲、乙两队单独完成各需多少天?
20.一小船由A港到B港顺流需行6 h,由B港到A港逆流需行8 h.一天,小船早晨6点由A港出发顺流到B港时,发现一救生圈在途中掉落在水中,立即返回,1 h后找到救生圈,问:(1)若小船按水流速度由A港到B港漂流需要多少小时?(2)救生圈是何时掉入水中的?
参考答案
1.C
2.C
3.B
4.C
5.A
6.D
7.C
8.C
9.<0
10.6
11.±(答案不唯一)
12.(答案不唯一)
13.
14.
15.(1)解:原式=a2 × × b × × × × =
(2)解:原式= = .
(3)解:原式= × = = - .
16.(1)解:3(x+1)-2(x-1)=1
3x+3-2x+2=1
x=-4
(2)解: + =
x2+5x-2=x2-x
6x=2
x=
17.解:这位同学的解答过程有错误,因为该同学求出由分式方程所化得的整式方程的解x=后,就认为x=应为原方程的解,事实上,若x==2时,原方程没有解,故应将x=2=排除.
解答过程应是:去分母得2x+a=-x+2,解这个方程得x=,由于原方程有正数解,故必有x=≠2,且x=>0,从而a≠-4,且a<2.即当a<2,且a≠-4时,原分式方程的解为正数.
18.解:设原来每天加固x米,
根据题意,得 + =9.
去分母,得 1 200+4 200=18x.
解得x=300.
检验:当x=300时,分母不等于0.
∴x=300是原方程的解.
答:该地驻军原来每天加固300米.
19.解:设乙队单独完成需x天,则甲队单独完成需x天,
由题意列方程得:+2( + )=1,
解得:x=6.
经检验x=6是原方程的解,x=4.
即甲队单独完成需4天,乙队单独完成需6天.
20.解:(1)设小船由A港漂流到B港需要x h,A港到B港距离为1,则水速为.
∴ - = + ,
解得x=48.
经检验x=48是原方程的根.
答:小船按水流速度由A港漂流到B港需要48 h.
(2)设救生圈y点落入水中,由问题(1)可知水流速度为,小船顺流由A港到B港用6 h,逆流走1 h,同时救生圈又顺流向前漂了1 h,
依题意有(12-y)( - ) = ( + ) ×1,解得y=11.
答:救生圈在中午11点落水.
相关文档
- 八年级下册数学教案16-2 第1课时 2021-11-012页
- 八年级下册数学同步练习第二十一章2021-11-014页
- 五年级下册数学试题-暑期衔接训练 2021-11-0110页
- 《同步课时卷》北师版八年级数学(下2021-11-016页
- 人民版《思想品德》八年级(下册)期中2021-11-018页
- 2019八年级数学上册 第13章 全等三2021-11-012页
- 2020八年级数学下册 专题突破讲练 2021-11-016页
- 八年级下册数学教案 第六章复习 2021-11-015页
- 2021秋北师大版八年级数学上册课件2021-11-0123页
- 八年级下册数学同步练习2-2-1 第22021-11-013页