2020春八年级数学下册第19章全等三角形19-4逆命题与逆定理3角平分线习题课件华东师大版 31页

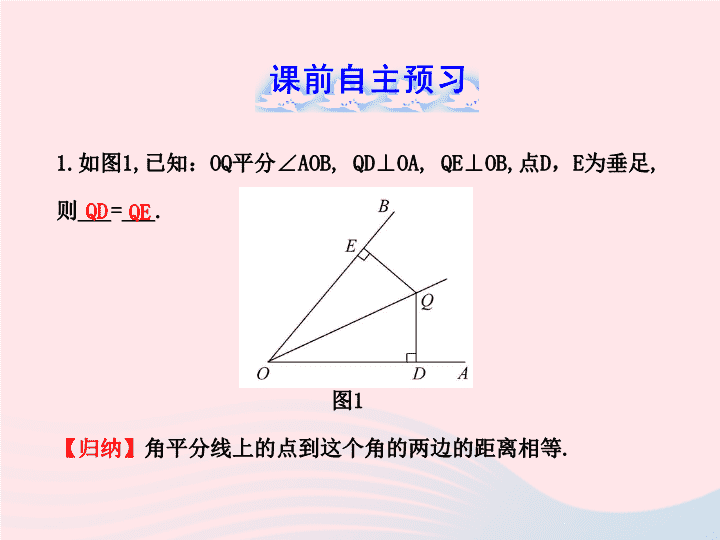
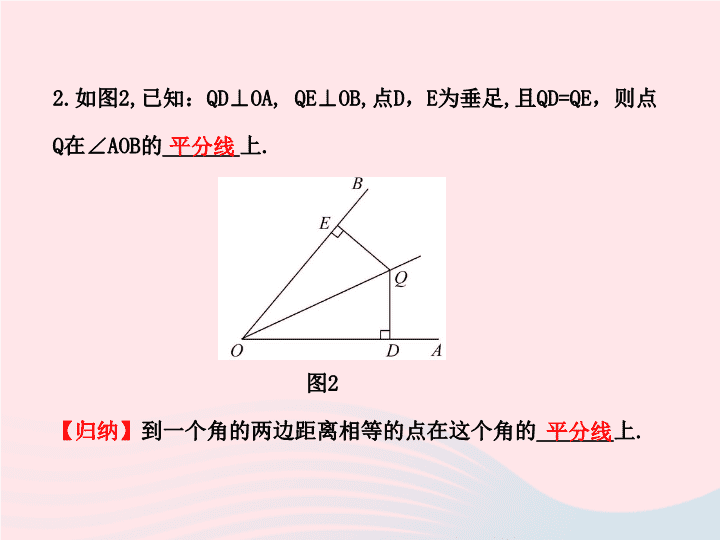
3. 角平分线 1. 如图 1, 已知： OQ 平分∠ AOB, QD⊥OA, QE⊥OB, 点 D ， E 为垂足 , 则 ___=___. 图 1 【 归纳 】 角平分线上的点到这个角的两边的距离相等 . QD QE 2. 如图 2, 已知： QD⊥OA, QE⊥OB, 点 D ， E 为垂足 , 且 QD=QE ，则点 Q 在∠ AOB 的 _______ 上 . 图 2 【 归纳 】 到一个角的两边距离相等的点在这个角的 _______ 上 . 平分线 平分线 3. 三角形三条角平分线交于 _____. 一点 【 预习思考 】 1. 角是轴对称图形吗？如果是，它的对称轴是什么 ? 提示： 角是轴对称图形，它的对称轴是角平分线所在的直线 . 2. 使用角平分线的判定定理要注意什么问题？ 提示： 要注意不能见到垂直就得结论，还要满足到角的两边距 离相等 , 二者缺一不可 . 角平分线性质定理和判定定理的应用 【 例 1】 如图 ,AD∥BC,∠ABC 的平分线 BP 与∠ BAD 的平分线 AP 相交 于点 P, 作 PE⊥AB 于点 E. 若 PE=2, 则两平行线 AD 与 BC 间的距离为 _________. 【 解题探究 】 1. 点 P 具备什么样的特点 ? 答 : 点 P 既在∠ ABC 的平分线上 , 又在∠ BAD 的平分线上 . 2. 根据点 P 具备的特点有什么样的性质 ? 依据是什么 ? 答 : 根据角平分线的性质 , 点 P 既到∠ ABC 的两边距离相等 , 又到 ∠ BAD 的两边距离相等 . 3. 根据上面的分析 , 解答问题 : 答 : 过点 P 作 MN⊥AD, 交 AD 于点 M, 交 BC 于点 N, 如图所示 : ∵AD∥BC,∠ABC 的平分线 BP 与∠ BAD 的平分线 AP 相交于点 P, PE⊥AB 于点 E, 又 PM⊥AD,PN⊥BC, ∴PM=PE=2,PN=PE=2,∴MN=2+2=4. 答案： 4 【 互动探究 】 1. 例题中的 PE 在解题的过程中起到了什么作用 ? 提示： 线段 PE 在解题的过程中起到了等量代换的作用 . 2. 改变∠ ABC 和∠ BAD 的大小 ( 保持∠ ABC+∠BAD=180°) 而不改 变 PE 值的大小 , 两平行线 AD 与 BC 间的距离变化吗 ? 提示： 不变 . 因为 MN=2PE. 与∠ ABC 和∠ BAD 的大小无关 . 【 规律总结 】 角平分线性质及判定的区别 附：记忆口诀： 角平分线性质记忆口诀 图中有角平分线 , 可向两边作垂线； 也可将图对折看 , 对折以后关系现 . 【 跟踪训练 】 1. 在以下结论中 , 不正确的是 ( ) (A) 平面内到角的两边距离相等的点一定在角平分线上 (B) 角平分线上任一点到角的两边的距离一定相等 (C) 一个角只有一条角平分线 (D) 角的平分线有时是直线 , 有时是线段 【 解析 】 选 D. 根据角平分线的判定及性质 , 选项 A ， B 正确；根据 角平分线的定义 , 得选项 C 正确 , 选项 D 错误 . 2. 如图 ,OP 是∠ AOB 的平分线 ,C 是 OP 上 一点 ,CE⊥OA 于点 E,CF⊥OB 于点 F, CE=6 cm,CF=_____cm, 理由是 ________ ______. 【 解析 】 OP 是∠ AOB 的平分线 ,CE⊥OA 于点 E,CF⊥OB 于点 F, 根据 角平分线的性质 , 得 CE=CF=6 cm, 理由 : 角平分线上的点到角的两 边距离相等 . 答案： 6 角平分线上的点到角的两边距离相等 3. 如图 , 已知 BD 是∠ ABC 的平分线 ,CD 是∠ ACB 的外角平分线 , 由 D 出发 , 作 点 D 到 BC ， AC 和 AB 的垂线 DE ， DF 和 DG, 垂足分别为 E ， F ， G, 则 DE ， DF ， DG 的 关系是 ________. 【 解析 】 因为 BD 是∠ ABC 的平分线 , CD 是∠ ACB 的外角平分线 , 且 DE⊥BC,DF⊥AC,DG⊥BA, 所以 ,DE=DF,DE=DG, 即 DE=DF=DG. 答案： DE=DF=DG 【 变式备选 】 如图 ,P 是∠ AOB 的平分线上的一个点 , PC⊥AO 于点 C,PD⊥OB 于点 D, 写出图中 一组相等的线段 __________( 只需写出 一组即可 ). 【 解析 】 因为 P 是∠ AOB 的平分线上的一个点 ,PC⊥AO,PD⊥OB, 所 以 PD=PC ；根据 H.L. 定理 , 得△ OPD≌△OPC, 所以 OD=OC. 答案： PD=PC ( 或 OD=OC) 角平分线性质定理和判定定理的综合应用 【 例 2】(6 分 ) 如图所示 , 在△ ABC 中 ,∠C=90°,BD 平分∠ ABC 交 AC 于点 D, 过点 D 作 DE∥BC 交 AB 于点 E, 过点 D 作 DF⊥AB 于点 F, 说明 BC=DE+EF 成立的理由 . 【 规范解答 】 ∵BD 平分∠ ABC,DF⊥AB,∠C 是直角 , ∴CD= DF ,∠DBC= ∠DBE ,∠DFB= ∠C , ………………………………… 1 分 ∴△ BCD≌ △BFD , ∴BC= BF . ……………………………………………………… 3 分 特别提醒 : 应是线段 DC 和 DF 相等，而不是 DC 和 DE 相等 . ∵DE∥BC, ∴∠DBC= ∠EDB , 又∵∠ DBC= ∠DBE , ∴∠EDB=∠DBE, ∴△BDE 是等腰三角形 , ……………………………………… 4 分 ∴ BE= DE , ∴BF=BC=DE+EF. ……………………………………………… 6 分 【 互动探究 】 例题中的△ EBD 具备什么特点 ? 提示： △ EBD 是等腰三角形 . 【 规律总结 】 角平分线 + 平行线 = 等腰三角形 角平分线平行线 , 等腰三角形来添 , 内错角加平分角 , 等角对应等线段 . 基本图形： P 是∠ CAB 的平分线上一点 ,PD∥AB, 则有∠ 1=∠2=∠3, 所以 AD=DP. 【 跟踪训练 】 4. 如图 ,△ABC 中 BD ， CD 平分∠ ABC ， ∠ ACB, 过 D 作直线平行于 BC, 分别交 AB ， AC 于 E ， F, 当∠ A 的位置及大小 变化时 , 线段 EF 和 BE+CF 的大小关系 ( ) (A)EF ＞ BE+CF (B)EF=BE+CF (C)EF ＜ BE+CF (D) 不能确定 【 解析 】 选 B. 根据 BD 平分∠ ABC 、 CD 平分∠ ACB, 且 EF∥BC, 得 △ BED 和△ CFD 是等腰三角形 , 即 ED=EB,FD=FC, 所以 EF=BE+CF, 与 ∠ A 的位置及大小变化无关 . 5. 如图 ,△ABC 中 ,∠ABC 的平分线与 ∠ ACB 外角的平分线交于点 D, 过 D 作 BC 的平行线交 AB ， AC 于 E ， F, 求证 : EF=BE-CF. 【 证明 】 ∵BD 平分∠ ABC,ED∥BC, ∴BE=DE. ∵CD 平分∠ ACG,ED∥BC, ∴∠FCD=∠FDC,∴FD=FC, ∴EF=DE-DF=BE-CF. 1. 如图 ,D 是∠ BAC 的平分线 AD 上一点 , DE⊥AB 于 E,DF⊥AC 于 F, 下列结论中 不正确的是 ( ) (A)DE=DF (B)AE=AF (C)△ADE≌△ADF (D)AD=DE+DF 【 解析 】 选 D. 根据角平分线的性质 , 选项 A 正确；又 AD=AD, 依据 H.L. 定理 , 得△ ADE≌△ADF, 即选项 B,C 正确；选项 D 不正确 . 2. 如图所示 , 已知∠ AOB=40°,OM 平分 ∠ AOB,MA⊥OA 于 A,MB⊥OB 于 B, 则∠ MAB 的度数为 ( ) (A)50° (B)40° (C)30° (D)20° 【 解析 】 选 D. 由 OM 平分∠ AOB,MA⊥OA,MB⊥OB, 得∠ AOM=20°, MA=MB, 所以∠ AMO=70°, 即∠ AMB=140°, 所以∠ MAB 故选 D. 3. 如图 ,∠AOB=30°,OP 平分∠ AOB,PC∥OB,PD⊥OB, 如果 PC=6, 那么 PD 等于 _________. 【 解析 】 过 P 作 PE⊥OA 于点 E, 如图 , 则 PD=PE.∵PC∥OB, ∴∠OPC=∠POD. ∵OP 平分∠ AOB,∠AOB=30°,∴∠ECP=30°. 在 Rt△ECP 中 , ∴PD=PE=3. 答案： 3 4. 如图 , 已知∠ CDA=∠CBA=90°, 且 CD=CB, 则点 C 在∠ _______ 的 平分线上 , 点 A 在∠ _______ 的平分线上 . 【 解析 】 ∵∠CDA=∠CBA=90°, 且 CD=CB, 根据角平分线性质的 逆定理 , 则点 C 在∠ BAD 的平分线上 , 点 A 在∠ BCD 的平分线上 . 答案： BAD BCD 5. 如图， P 是∠ BAC 内的一点， PE⊥AB,PF⊥AC, 垂足分别为点 E,F,AE=AF. 求证： (1)PE=PF ； (2) 点 P 在∠ BAC 的平分线上 . 【 证明 】 (1) 如图，连结 AP ， ∵ PE⊥AB,PF⊥AC, ∴∠AEP=∠AFP=90°. 又 AE=AF ， AP=AP ， ∴ Rt△AEP≌Rt△AFP ， ∴ PE=PF ； (2)∵Rt△AEP≌Rt△AFP ， ∴∠ EAP=∠FAP ， ∴ AP 是∠ BAC 的平分线， 故点 P 在∠ BAC 的平分线上 .