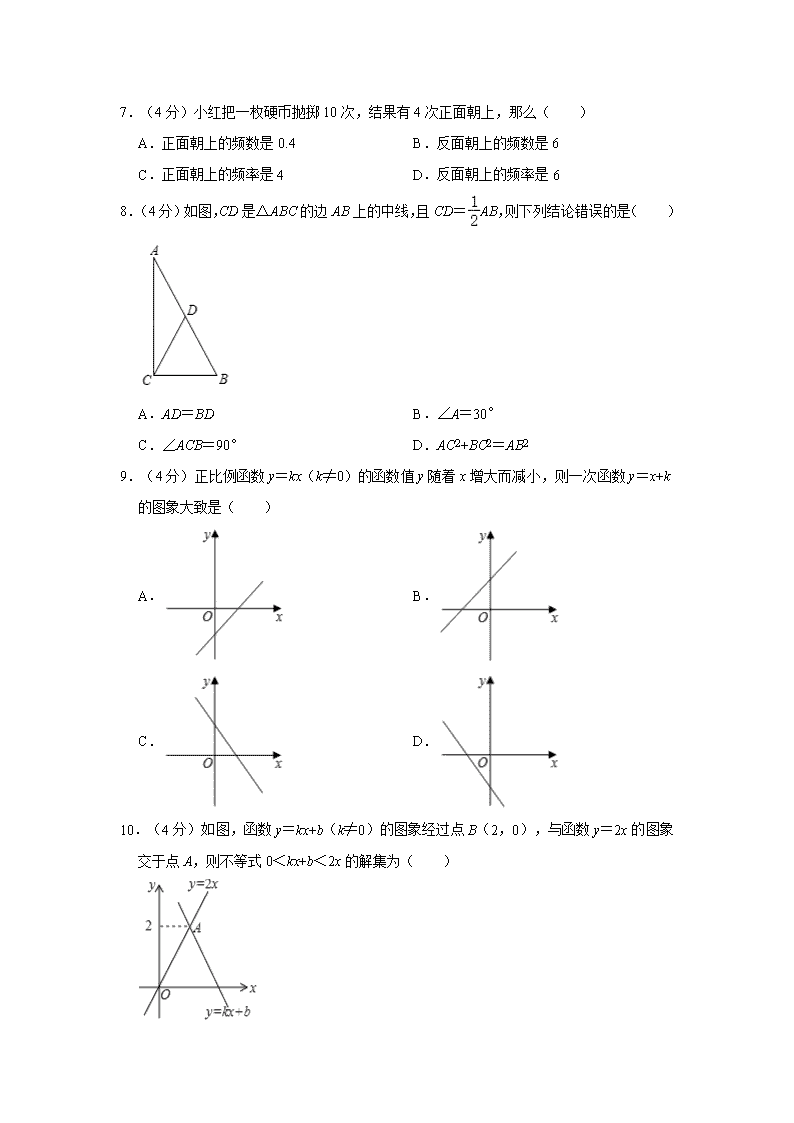2019-2020学年湖南省益阳市赫山区八年级（下）期末数学试卷 解析版 23页

‎2019-2020学年湖南省益阳市赫山区八年级（下）期末数学试卷 一、选择题：本题共10小题，每小题4分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（4分）下列几组数中，能作为直角三角形三边长度的是（　　）‎ A．2，3，4 B．4，4，5 C．5，6，7 D．5，12，13‎ ‎2．（4分）剪纸是我国的非物质文化遗产之一，下列剪纸作品中是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎3．（4分）若一个多边形的每个内角都等于150°，则这个多边形的边数是（　　）‎ A．10 B．11 C．12 D．13‎ ‎4．（4分）顺次连接矩形的各边中点，所得的四边形一定是（　　）‎ A．正方形 B．菱形 C．矩形 D．梯形 ‎5．（4分）在平面直角坐标系中，点P（﹣3，4）关于x轴的对称点的坐标是（　　）‎ A．（﹣4，﹣3） B．（﹣3，﹣4） C．（3，4） D．（3，﹣4）‎ ‎6．（4分）如图，在平面直角坐标系中，平行四边形ABCD的顶点A、B、D的坐标分别是（0，0）、（5，0）、（2，3），则点C的坐标是（　　）‎ A．（8，2） B．（5，3） C．（7，3） D．（3，7）‎ ‎7．（4分）小红把一枚硬币抛掷10次，结果有4次正面朝上，那么（　　）‎ A．正面朝上的频数是0.4 B．反面朝上的频数是6 ‎ C．正面朝上的频率是4 D．反面朝上的频率是6‎ ‎8．（4分）如图，CD是△ABC的边AB上的中线，且CD＝AB，则下列结论错误的是（　　）‎ A．AD＝BD B．∠A＝30° ‎ C．∠ACB＝90° D．AC2+BC2＝AB2‎ ‎9．（4分）正比例函数y＝kx（k≠0）的函数值y随着x增大而减小，则一次函数y＝x+k的图象大致是（　　）‎ A． B． ‎ C． D．‎ ‎10．（4分）如图，函数y＝kx+b（k≠0）的图象经过点B（2，0），与函数y＝2x的图象交于点A，则不等式0＜kx+b＜2x的解集为（　　）‎ A．x＞0 B．0＜x＜1 C．1＜x＜2 D．x＞2‎ 二、填空题：本题共8小题，每小题4分，把答案填在答题卡中对应题号后的横线上.‎ ‎11．（4分）如图，在△ABC中，∠C＝90°，AD平分∠CAB，BC＝6，BD＝4，则点D到AB的距离是　 　．‎ ‎12．（4分）五边形从某一个顶点出发可以引　 　条对角线．‎ ‎13．（4分）已知菱形的两对角线长分别为6cm和8cm，则菱形的面积为　 　cm2．‎ ‎14．（4分）将点P（﹣3，4）先向下平移3个单位，再向右平移2个单位后得到点Q，则点Q的坐标是　 　．‎ ‎15．（4分）在函数y＝中，自变量x的取值范围是　 　．‎ ‎16．（4分）今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间．设他从山脚出发后所用时间为t（分钟），所走的路程为s（米），s与t之间的函数关系如图所示．则下列说法中，正确的序号为　 　．‎ ‎①小明中途休息用了20分钟．‎ ‎②小明休息前爬山的平均速度为每分钟70米．‎ ‎③小明在上述过程中所走的路程为6600米．‎ ‎④小明休息前爬山的平均速度大于休息后爬山的平均速度．‎ ‎17．（4分）一次函数y＝kx+b（k≠0）中，x与y的部分对应值如表：‎ x ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ y ‎9‎ ‎6‎ ‎3‎ ‎0‎ ‎﹣3‎ 那么，一元一次方程kx+b＝0的解为　 　．‎ ‎18．（4分）如图Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，点P为BC 上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ的最小值为　 　．‎ 三、解答题：本题共8小题，共78分，解答应写出文字说明、证明过程或演算步骤.‎ ‎19．（8分）如图，在△ABC中，∠C＝90°，∠A＝30°，BD是∠ABC的平分线，CD＝5cm，求AB的长．‎ ‎20．（8分）已知：如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于F、F．求证：四边形AFCE是菱形．‎ ‎21．（8分）在平面直角坐标系xOy中，已知直线l：y＝kx+b（k≠0经过点A（﹣4，0），与y轴交于点B，如果△AOB的面积为4，求直线l的表达式．‎ ‎22．（10分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．‎ ‎（1）请画出△ABC向左平移5个单位长度后得到的△A1B1C1；‎ ‎（2）请画出△ABC关于原点对称的△A2B2C2；‎ ‎（3）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．‎ ‎23．（10分）某班同学为了解2019年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理．‎ 月均用水量 频数 频率 ‎0＜x≤5‎ ‎6‎ ‎0.12‎ ‎5＜x≤10‎ m ‎0.24‎ ‎10＜x≤15‎ ‎16‎ ‎0.32‎ ‎15＜x≤20‎ ‎10‎ ‎0.20‎ ‎20＜x≤25‎ ‎4‎ n ‎25＜x≤30‎ ‎2‎ ‎0.04‎ 请解答以下问题：‎ ‎（1）求出上面的频数分布表中的m、n的值，并把频数分布直方图补充完整；‎ ‎（2）求该小区用水量不超过15t的家庭占被调查家庭总数的百分比；‎ ‎（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过10t的家庭大约有多少户？‎ ‎24．（10分）阅读与探究 我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．‎ 请结合上述阅读材料，解决下列问题：‎ ‎（1）在我们所学过的特殊四边形中，是勾股四边形的是　 　；（写出一种即可）‎ ‎（2）下面图1，图2均为6×6的正方形网格，点A，B，C均在格点上，请在图中标出格点D，并连接AD，CD，使得四边形ABCD符合下列要求：图1中的四边形ABCD是勾股四边形，并且是中心对称图形；图2中的四边形ABCD是勾股四边形且对角线相等，但不是中心对称图形．‎ ‎25．（12分）如图，已知四边形ABCD是正方形，点E、F分别在AD、DC上，BE与AF相交于点G，且BE＝AF．‎ ‎（1）求证：△ABE≌△DAF；‎ ‎（2）求证：BE⊥AF；‎ ‎（3）如果正方形ABCD的边长为5，AE＝2，点H为BF的中点，连接GH．求GH的长．‎ ‎26．（12分）如表是某摩托车厂2019年前3个月摩托车各月产量：‎ x（月）‎ ‎1‎ ‎2‎ ‎3‎ y（辆）‎ ‎550‎ ‎600‎ ‎650‎ ‎（1）根据表格中的数据，求y（辆）与x（月）之间的函数表达式；‎ ‎（2）按照此趋势，你能预测该摩托车厂2019年4月摩托车月产量吗？‎ ‎（3）能够利用（1）中所建立函数模型预测2019年12月摩托车月产量吗？为什么？‎ ‎2019-2020学年湖南省益阳市赫山区八年级（下）期末数学试卷 参考答案与试题解析 一、选择题：本题共10小题，每小题4分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（4分）下列几组数中，能作为直角三角形三边长度的是（　　）‎ A．2，3，4 B．4，4，5 C．5，6，7 D．5，12，13‎ ‎【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形判定则可．‎ ‎【解答】解：A、∵22+32≠42，∴不能构成直角三角形；‎ B、∵42+42≠52，∴不能构成直角三角形；‎ C、∵52+62≠72，∴不能构成直角三角形；‎ D、∵52+122＝132，∴能构成直角三角形．‎ 故选：D．‎ ‎2．（4分）剪纸是我国的非物质文化遗产之一，下列剪纸作品中是中心对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据中心对称图形的概念对各选项分析判断即可得解．‎ ‎【解答】解：A、是中心对称图形，故本选项正确；‎ B、不是中心对称图形，故本选项错误；‎ C、不是中心对称图形，故本选项错误；‎ D、不是中心对称图形，故本选项错误．‎ 故选：A．‎ ‎3．（4分）若一个多边形的每个内角都等于150°，则这个多边形的边数是（　　）‎ A．10 B．11 C．12 D．13‎ ‎【分析】根据多边形的内角和定理：180°•（n﹣2）求解即可．‎ ‎【解答】解：由题意可得：180°•（n﹣2）＝150°•n，‎ 解得n＝12．‎ 故多边形是12边形．‎ 故选：C．‎ ‎4．（4分）顺次连接矩形的各边中点，所得的四边形一定是（　　）‎ A．正方形 B．菱形 C．矩形 D．梯形 ‎【分析】根据菱形的定义：只需证明四边相等即可．‎ ‎【解答】解：顺次连接矩形的各边中点，根据矩形的对角线相等和中位线定理可知所得的四边形四边相等，所以是菱形．‎ 故选：B．‎ ‎5．（4分）在平面直角坐标系中，点P（﹣3，4）关于x轴的对称点的坐标是（　　）‎ A．（﹣4，﹣3） B．（﹣3，﹣4） C．（3，4） D．（3，﹣4）‎ ‎【分析】平面直角坐标系中任意一点P（x，y），关于x轴的对称点的坐标是（x，﹣y），即关于横轴的对称点，横坐标不变，纵坐标变成相反数，这样就可以求出对称点的坐标．‎ ‎【解答】解：点A（﹣3，4）关于x轴的对称点的坐标是（﹣3，﹣4），‎ 故选：B．‎ ‎6．（4分）如图，在平面直角坐标系中，平行四边形ABCD的顶点A、B、D的坐标分别是（0，0）、（5，0）、（2，3），则点C的坐标是（　　）‎ A．（8，2） B．（5，3） C．（7，3） D．（3，7）‎ ‎【分析】平行四边形的对边相等且互相平行，所以AB＝CD，AB＝5，D 的横坐标为2，加上5为7，所以C的横坐标为7，因为CD∥AB，D的纵坐标和C的纵坐标相同为3．‎ ‎【解答】解：在平行四边形ABCD中，‎ ‎∵AB∥CDAB＝5，‎ ‎∴CD＝5，‎ ‎∵D点的横坐标为2，‎ ‎∴C点的横坐标为2+5＝7，‎ ‎∵AB∥CD，‎ ‎∴D点和C点的纵坐标相等为3，‎ ‎∴C点的坐标为（7，3）．‎ 故选：C．‎ ‎7．（4分）小红把一枚硬币抛掷10次，结果有4次正面朝上，那么（　　）‎ A．正面朝上的频数是0.4 B．反面朝上的频数是6 ‎ C．正面朝上的频率是4 D．反面朝上的频率是6‎ ‎【分析】根据实验结果得出结论即可．‎ ‎【解答】解：小红做抛硬币的实验，共抛了10次，4次正面朝上，6次反面朝上，则正面朝上的频数是4，反面朝上的频数是6，‎ 故选：B．‎ ‎8．（4分）如图，CD是△ABC的边AB上的中线，且CD＝AB，则下列结论错误的是（　　）‎ A．AD＝BD B．∠A＝30° ‎ C．∠ACB＝90° D．AC2+BC2＝AB2‎ ‎【分析】根据CD是△ABC的边AB上的中线，且CD＝AB，可以得到AD、BD和CD的关系，从而可以判断A是否正确，再根据等腰三角形的性质和三角形内角和，可以得到∠ACB的度数，从而可以得到∠ACB的度数，即可判断C 是否正确，最后根据勾股定理，可以判断D是否正确；对于∠A，由题目中的条件，无法判断角的度数，从而可以判断B是否正确．‎ ‎【解答】解：∵CD是△ABC的边AB上的中线，且CD＝AB，‎ ‎∴AD＝BD＝CD，故选项A正确，‎ ‎∴∠1＝∠2，∠3＝∠4，‎ ‎∵∠1+∠2+∠3+∠4＝180°，‎ ‎∴∠2+∠3＝90°，‎ 即∠ACB＝90°，故选项C正确；‎ ‎∴AC2+BC2＝AB2，故选项D正确；‎ 无法判断∠A的度数，故选项B错误；‎ 故选：B．‎ ‎9．（4分）正比例函数y＝kx（k≠0）的函数值y随着x增大而减小，则一次函数y＝x+k的图象大致是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据正比例函数的性质得到k＜0，然后根据一次函数的性质得到一次函数y＝x+k的图象经过第一、三象限，且与y轴的负半轴相交．‎ ‎【解答】解：∵正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，‎ ‎∴k＜0，‎ ‎∵一次函数y＝x+k的一次项系数大于0，常数项小于0，‎ ‎∴一次函数y＝x+k的图象经过第一、三象限，且与y轴的负半轴相交．‎ 故选：A．‎ ‎10．（4分）如图，函数y＝kx+b（k≠0）的图象经过点B（2，0），与函数y＝2x的图象交于点A，则不等式0＜kx+b＜2x的解集为（　　）‎ A．x＞0 B．0＜x＜1 C．1＜x＜2 D．x＞2‎ ‎【分析】先利用正比例函数解析式确定A点坐标，然后观察函数图象得到，当1＜x＜2时，直线y＝2x都在直线y＝kx+b的上方，于是可得到不等式0＜kx+b＜2x的解集．‎ ‎【解答】解：把A（x，2）代入y＝2x得2x＝2，解得x＝1，则A点坐标为（1，2），‎ 所以当x＞1时，2x＞kx+b，‎ ‎∵函数y＝kx+b（k≠0）的图象经过点B（2，0），‎ 即不等式0＜kx+b＜2x的解集为1＜x＜2．‎ 故选：C．‎ 二、填空题：本题共8小题，每小题4分，把答案填在答题卡中对应题号后的横线上.‎ ‎11．（4分）如图，在△ABC中，∠C＝90°，AD平分∠CAB，BC＝6，BD＝4，则点D到AB的距离是　2　．‎ ‎【分析】首先根据已知易求CD＝2，利用角平分线的性质可得点D到AB的距离是2．‎ ‎【解答】解：∵BC＝6，BD＝4‎ ‎∴CD＝2‎ ‎∵∠C＝90°，AD平分∠CAB ‎∴点D到AB的距离＝CD＝2．‎ 故填2．‎ ‎12．（4分）五边形从某一个顶点出发可以引　2　条对角线．‎ ‎【分析】从n边形的一个顶点出发有（n﹣3）条对角线，代入求出即可．‎ ‎【解答】解：从五边形的一个顶点出发有5﹣3＝2条对角线，‎ 故答案为：2．‎ ‎13．（4分）已知菱形的两对角线长分别为6cm和8cm，则菱形的面积为　24　cm2．‎ ‎【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可．‎ ‎【解答】解：由已知得，菱形的面积等于两对角线乘积的一半 即：6×8÷2＝24cm2．‎ 故答案为：24．‎ ‎14．（4分）将点P（﹣3，4）先向下平移3个单位，再向右平移2个单位后得到点Q，则点Q的坐标是　（﹣1，1）　．‎ ‎【分析】根据横坐标，右移加，左移减；纵坐标，上移加，下移减可得答案．‎ ‎【解答】解：根据题意，知点Q的坐标是（﹣3+2，4﹣3），即（﹣1，1），‎ 故答案为：（﹣1，1）．‎ ‎15．（4分）在函数y＝中，自变量x的取值范围是　x＞1.5　．‎ ‎【分析】根据被开方数大于等于0，分母不等于0列式计算即可得解．‎ ‎【解答】解：由题意得2x﹣3＞0，‎ 解得x＞1.5．‎ 故答案为：x＞1.5．‎ ‎16．（4分）今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间．设他从山脚出发后所用时间为t（分钟），所走的路程为s（米），s与t之间的函数关系如图所示．则下列说法中，正确的序号为　①②④　．‎ ‎①小明中途休息用了20分钟．‎ ‎②小明休息前爬山的平均速度为每分钟70米．‎ ‎③小明在上述过程中所走的路程为6600米．‎ ‎④小明休息前爬山的平均速度大于休息后爬山的平均速度．‎ ‎【分析】根据函数图象可知，小明40分钟爬山2800米，40～60分钟休息，60～100分钟爬山（3800﹣2800）米，爬山的总路程为3800米，根据路程、速度、时间的关系进行解答即可．‎ ‎【解答】解：①、根据图象可知，在40～60分钟，路程没有发生变化，所以小明中途休息的时间为：60﹣40＝20分钟，故正确；‎ ‎②、根据图象可知，当t＝40时，s＝2800，所以小明休息前爬山的平均速度为：2800÷40＝70（米/分钟），故B正确；‎ ‎③、根据图象可知，小明在上述过程中所走的路程为3800米，故错误；‎ ‎④、小明休息后的爬山的平均速度为：（3800﹣2800）÷（100﹣60）＝25（米/分），小明休息前爬山的平均速度为：2800÷40＝70（米/分钟），‎ ‎70＞25，所以小明休息前爬山的平均速度大于休息后爬山的平均速度，故正确；‎ 综上所述，正确的有①②④．‎ 故答案为：①②④‎ ‎17．（4分）一次函数y＝kx+b（k≠0）中，x与y的部分对应值如表：‎ x ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1‎ ‎2‎ y ‎9‎ ‎6‎ ‎3‎ ‎0‎ ‎﹣3‎ 那么，一元一次方程kx+b＝0的解为　x＝1　．‎ ‎【分析】利用函数值为0时对应的自变量的值为方程kx+b＝0（k≠0）的解得到答案．‎ ‎【解答】解：∵x＝1时，y＝0，‎ ‎∴一元一次方程kx+b＝0的解为x＝1．‎ 故答案为x＝1．‎ ‎18．（4分）如图Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4，点P为BC上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ的最小值为　　．‎ ‎【分析】以PA，PC为邻边作平行四边形PAQC，由平行四边形的性质可知O是AC中点，PQ最短也就是PO最短，所以应该过O作BC的垂线P′O，然后根据△P′OC和△ABC相似，利用相似三角形的性质即可求出PQ的最小值．‎ ‎【解答】解：∵∠BAC＝90°，AB＝3，AC＝4，‎ ‎∴BC＝＝5，‎ ‎∵四边形APCQ是平行四边形，‎ ‎∴PO＝QO，CO＝AO，‎ ‎∵PQ最短也就是PO最短，‎ ‎∴过O作BC的垂线OP′，‎ ‎∵∠ACB＝∠P′CO，∠CP′O＝∠CAB＝90°，‎ ‎∴△CAB∽△CP′O，‎ ‎∴，‎ ‎∴，‎ ‎∴OP′＝，‎ ‎∴则PQ的最小值为2OP′＝，‎ 故答案为：．‎ 三、解答题：本题共8小题，共78分，解答应写出文字说明、证明过程或演算步骤.‎ ‎19．（8分）如图，在△ABC中，∠C＝90°，∠A＝30°，BD是∠ABC的平分线，CD ‎＝5cm，求AB的长．‎ ‎【分析】根据角平分线的定义、直角三角形的性质计算．‎ ‎【解答】解：在Rt△ABC中，∠C＝90°，∠A＝∠30°，‎ ‎∴∠ABC＝60°．‎ ‎∵BD是∠ABC的平分线，‎ ‎∴∠ABD＝∠CBD＝30°．‎ ‎∴∠ABD＝∠BAD，‎ ‎∴AD＝DB，‎ 在Rt△CBD中，CD＝5cm，∠CBD＝30°，‎ ‎∴BD＝10cm．‎ 由勾股定理得，BC＝5，‎ ‎∴AB＝2BC＝10cm．‎ ‎20．（8分）已知：如图，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于F、F．求证：四边形AFCE是菱形．‎ ‎【分析】根据EF是对角线AC的垂直平分线，可以求证△AOE≌△COF，证明四边形的对角线互相平分，垂直，就可以证出．‎ ‎【解答】解：∵EF是对角线AC的垂直平分线，‎ ‎∴OA＝OC，AC⊥EF，‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴AD∥BC，‎ ‎∴∠EAO＝∠FCO，‎ ‎∵∠AOE＝∠COF，‎ ‎∴在△AOE和△COF中，‎ ‎∴△AOE≌△COF（ASA）．‎ ‎∴OE＝OF．‎ ‎∴四边形AFCE是平行四边形，‎ 又∵AC⊥EF，‎ ‎∴四边形是AFCE菱形．‎ ‎21．（8分）在平面直角坐标系xOy中，已知直线l：y＝kx+b（k≠0经过点A（﹣4，0），与y轴交于点B，如果△AOB的面积为4，求直线l的表达式．‎ ‎【分析】先把A点坐标代入y＝kx+b得到b＝4k，则y＝kx+4k，所以B（0，4k），利用三角形面积公式得到×4×|4k|＝4，解得k＝或﹣，从而得到直线l的表达式．‎ ‎【解答】解：把A（﹣4，0）代入y＝kx+b得﹣4k+b＝0，解得b＝4k，‎ ‎∴y＝kx+4k，‎ 当x＝0时，y＝kx+4k+4k，则B（0，4k），‎ ‎∵△AOB的面积为4，‎ ‎∴×4×|4k|＝4，解得k＝或﹣，‎ ‎∴直线l的表达式为y＝x+2或y＝﹣x﹣2．‎ ‎22．（10分）如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．‎ ‎（1）请画出△ABC向左平移5个单位长度后得到的△A1B1C1；‎ ‎（2）请画出△ABC关于原点对称的△A2B2C2；‎ ‎（3）在x轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标．‎ ‎【分析】（1）根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置，然后顺次连接即可；‎ ‎（2）根据网格结构找出点A、B、C关于原点的对称点A2、B2、C2的位置，然后顺次连接即可；‎ ‎（3）找出点A关于x轴的对称点A′，连接A′B与x轴相交于一点，根据轴对称确定最短路线问题，交点即为所求的点P的位置，然后连接AP、BP并根据图象写出点P的坐标即可．‎ ‎【解答】解：（1）△A1B1C1如图所示；‎ ‎（2）△A2B2C2如图所示；‎ ‎（3）△PAB如图所示，P（2，0）．‎ ‎23．（10分）某班同学为了解2019年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理．‎ 月均用水量 频数 频率 ‎0＜x≤5‎ ‎6‎ ‎0.12‎ ‎5＜x≤10‎ m ‎0.24‎ ‎10＜x≤15‎ ‎16‎ ‎0.32‎ ‎15＜x≤20‎ ‎10‎ ‎0.20‎ ‎20＜x≤25‎ ‎4‎ n ‎25＜x≤30‎ ‎2‎ ‎0.04‎ 请解答以下问题：‎ ‎（1）求出上面的频数分布表中的m、n的值，并把频数分布直方图补充完整；‎ ‎（2）求该小区用水量不超过15t的家庭占被调查家庭总数的百分比；‎ ‎（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过10t的家庭大约有多少户？‎ ‎【分析】（1）根据0＜x≤5中频数为6，频率为0.12，则调查总户数为6÷0.12＝50，进而得出在5＜x≤10范围内的频数以及在20＜x≤25范围内的频率；‎ ‎（2）根据（1）中所求即可得出不超过15t的家庭总数即可求出，不超过15t的家庭占被调查家庭总数的百分比；‎ ‎（3）根据样本数据中超过10t的家庭数，即可得出1000户家庭超过10t的家庭数．‎ ‎【解答】解：（1）∵被调查的总户数为6÷0.12＝50（户），‎ ‎∴m＝50×0.24＝12，n＝4÷50＝0.08，‎ 补全频数分布直方图如下：‎ ‎（2）该小区用水量不超过15t的家庭占被调查家庭总数的百分比为0.12+0.24+0.32＝0.68＝68%；‎ ‎（3）该小区月均用水量超过10t的家庭大约有1000×（1﹣0.12﹣0.24）＝640（户）．‎ ‎24．（10分）阅读与探究 我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．‎ 请结合上述阅读材料，解决下列问题：‎ ‎（1）在我们所学过的特殊四边形中，是勾股四边形的是　矩形　；（写出一种即可）‎ ‎（2）下面图1，图2均为6×6的正方形网格，点A，B，C均在格点上，请在图中标出格点D，并连接AD，CD，使得四边形ABCD符合下列要求：图1中的四边形ABCD是勾股四边形，并且是中心对称图形；图2中的四边形ABCD是勾股四边形且对角线相等，但不是中心对称图形．‎ ‎【分析】（1）根据勾股四边形的定义判断即可．‎ ‎（2）根据要求结合数形结合的思想画出图形即可．‎ ‎【解答】解：（1）矩形是勾股四边形．‎ 故答案为：矩形．‎ ‎（2）如图1中，四边形ABCD即为所求．‎ 如图2中，四边形ABCD即为所求．‎ ‎25．（12分）如图，已知四边形ABCD是正方形，点E、F分别在AD、DC上，BE与AF相交于点G，且BE＝AF．‎ ‎（1）求证：△ABE≌△DAF；‎ ‎（2）求证：BE⊥AF；‎ ‎（3）如果正方形ABCD的边长为5，AE＝2，点H为BF的中点，连接GH．求GH的长．‎ ‎【分析】（1）根据正方形的四条边都相等可得AB＝AD，每一个角都是直角可得∠BAE＝∠D＝90°，然后利用“斜边直角边”证明Rt△ABE≌Rt△DAF；‎ ‎（2）结合（1）得∠ABE＝∠DAF，进一步得∠AGE＝∠BGF＝90°即可；‎ ‎（3）根据直角三角形斜边上的中线等于斜边的一半得GH＝BF，利用勾股定理求出BF的长即可得出答案．‎ ‎【解答】解：（1）证明：∵四边形ABCD为正方形，‎ ‎∴∠BAE＝∠D＝90°，AB＝AD，‎ 在Rt△ABE和Rt△DAF中，‎ ‎，‎ ‎∴Rt△ABE≌Rt△DAF（HL）；‎ ‎（2）证明：∵Rt△ABE≌Rt△DAF，‎ ‎∴∠ABE＝∠DAF，‎ ‎∵∠ABE+∠BEA＝90°，‎ ‎∴∠DAF+∠BEA＝90°，‎ ‎∴∠AGE＝∠BGF＝90°，‎ ‎∴BE⊥AF；‎ ‎（3）∵BE⊥AF，‎ ‎∵点H为BF的中点，‎ ‎∴GH＝BF，‎ ‎∵在Rt△BCF中，BC＝5，CF＝CD﹣DF＝5﹣2＝3，根据勾股定理，得 ‎∴BF＝＝，‎ ‎∴GH＝．‎ ‎26．（12分）如表是某摩托车厂2019年前3个月摩托车各月产量：‎ x（月）‎ ‎1‎ ‎2‎ ‎3‎ y（辆）‎ ‎550‎ ‎600‎ ‎650‎ ‎（1）根据表格中的数据，求y（辆）与x（月）之间的函数表达式；‎ ‎（2）按照此趋势，你能预测该摩托车厂2019年4月摩托车月产量吗？‎ ‎（3）能够利用（1）中所建立函数模型预测2019年12月摩托车月产量吗？为什么？‎ ‎【分析】（1）根据表格中的数据，可以求得y（辆）与x（月）之间的函数表达式；‎ ‎（2）根据（1）中的函数关系式，可以得到该摩托车厂2019年4月摩托车月产量；‎ ‎（3）本题答案不唯一，只要说的理由合理即可．‎ ‎【解答】解：（1）设y（辆）与x（月）之间的函数表达式y＝kx+b，‎ ‎，‎ 解得，，‎ 即y（辆）与x（月）之间的函数表达式y＝50x+500；‎ ‎（2）当x＝4时，y＝50×4+500＝700，‎ 即该摩托车厂2019年4月摩托车月产量700辆；‎ ‎（3）不能利用（1）中所建立函数模型预测2019年12月摩托车月产量，‎ 理由：因为前三个月的产量与12月份相差较远，随着月份的变化，人们对摩托车的需求量也不一样，故不能利用（1）中所建立函数模型预测2019年12月摩托车月产量．‎