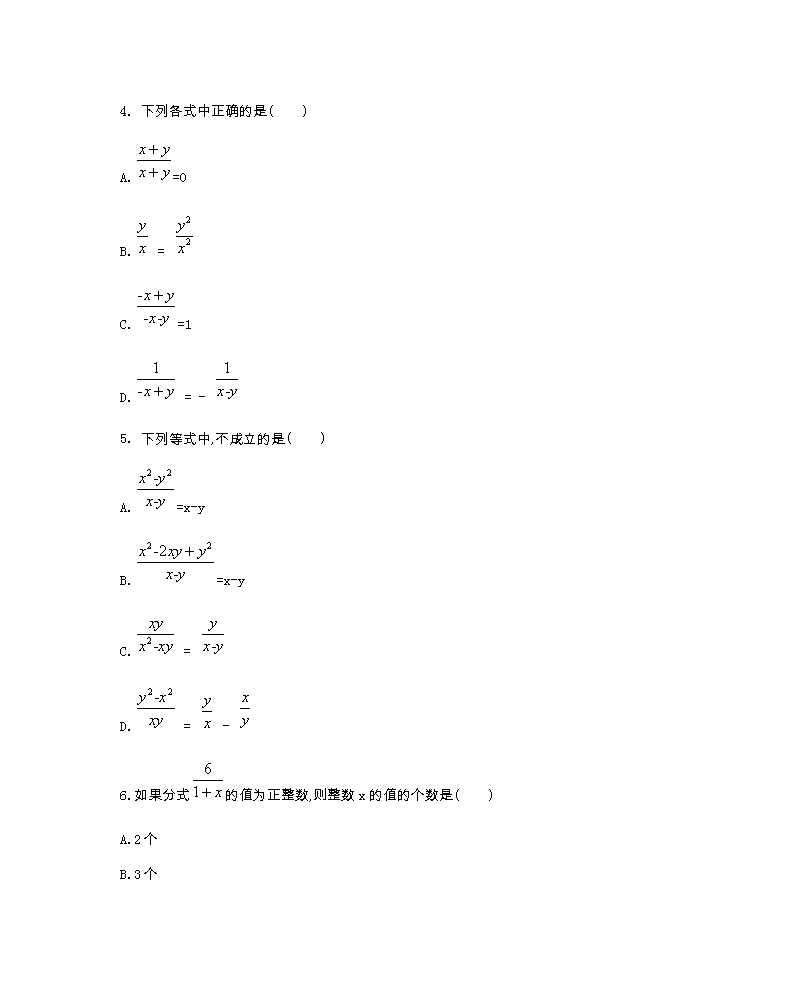北师大版八年级数学（下册）第五章测试卷（附答案） 10页

北师八下数学测试卷第五章 ‎ ‎1. 使分式有意义的x的取值范围是(　　)‎ A.x=2‎ B.x≠2‎ C.x=-2‎ D.x≠-2‎ ‎2. 已知两个分式：A=,B= + ,其中x≠±2,则A与B 的关系是(　　)‎ A.相等 B.互为倒数 C.互为相反数 D.A大于B ‎3. 下列各式从左到右变形正确的是(　　)‎ A. + =3(x+1)+2y B. = ‎ C. = ‎ D. = ‎ ‎4. 下列各式中正确的是(　　)‎ A.=0‎ B. = ‎ C.=1‎ D. = - ‎ ‎5. 下列等式中,不成立的是(　　)‎ A.=x-y B.=x-y C. = ‎ D. = - ‎ ‎6.如果分式的值为正整数,则整数x的值的个数是(　　)‎ A.2个 B.3个 C.4个 ‎ D.5个 ‎ ‎7.把a千克盐溶于b千克水中,得到一种盐水,若有这种盐水x千克,则其中含盐(　　)‎ A.千克 ‎ B.千克 C.千克 D.千克 ‎8 .把分式方程 - =1的两边同时乘以x-2,约去分母,得(　　)‎ A.1-(1-x)=1‎ B.1+(1-x)=1‎ C.1-(1-x)=x-2‎ D.1+(1-x)=x-2‎ ‎9.化简： ÷ ·的结果是　　　　　　　. ‎ ‎10.计算：x· ÷ ·y=　　　　　　　.‎ ‎11.已知当x=-2时,分式无意义,x=4时,此分式的值为0,则a+b=　　　　　　.‎ ‎12.一项工程,甲单独做x小时完成,乙单独做y小时完成,则两人一起完成这项工程需要 　　　　　　　小时. ‎ ‎13.已知 - = ,则的值是　　　　　　　　.‎ ‎14.若 - =0无解,则m的值是　　　　　　　.‎ ‎15.解答题.‎ ‎(1)约分：① ‎ ‎② ‎ ‎(2)通分：① ,,-‎ ‎② ,,‎ ‎16.(1)要使分式的值为零,x和y的取值范围是什么?‎ ‎(2)已知： + = ,求 + 的值.‎ ‎17. 解方程.‎ ‎(1) = ‎ ‎(2) + =1‎ ‎18.解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.‎ ‎(1)设A= - ,B=,求A与B的积;‎ ‎(2)提出(1)的一个“逆向”问题,并解答这个问题.‎ ‎19.A,B两地相距80千米,一辆公共汽车从A地出发开往B地,2小时后,又从A地开来一辆小汽车,小汽车的速度是公共汽车的3倍.结果小汽车比公共汽车早40分钟到达B地.求两种车的速度.‎ ‎20.关于x的方程：x+ =c + 的解是x1=c,x2=;‎ x- = c- (即 + = c + )的解是x1=c,x2=-;‎ x+ = c + 的解是x1=c,x2=;‎ x+ = c + 的解是x1=c,x2=;…‎ ‎(1)请观察上述方程与解的特征,比较关于x的方程x+ = c+ (m≠0)与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.‎ ‎(2)由上述的观察、比较、猜想、验证,可以得出结论：如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程：x+ = a + .‎ 参考答案 ‎1.B ‎2.C ‎3.C ‎4.D ‎5.A ‎6.C ‎7.A ‎8.D ‎9.b3‎ ‎10.xy ‎11.2‎ ‎12.‎ ‎13.-2‎ ‎14.3‎ ‎15.(1)解： ①-‎ ‎② ‎ ‎(2)解：①最简公分母是36a4b3,- ,,-. ‎ ‎②最简公分母是(x+2)(x-2),,,-.‎ ‎16.(1)解： x=-1且y≠±1.‎ ‎(2)解：-1‎ ‎17.(1)解：x=3‎ ‎(2)解：x=‎ ‎18. 解：(1)A·B=( - ) × = × =2x+8.‎ ‎(2)答案不唯一.如,“逆向”问题一：已知A·B=2x+8,B=,求A. ‎ 解答：A=(A·B)÷B=(2x+8)÷ = .‎ ‎“逆向”问题二：已知A·B=2x+8,A= - .求B.‎ 解答：B=(A·B)÷A=(2x+8)÷( - ) =(2x+8) ÷ =2(x+4)× = .‎ ‎19. 解：设公共汽车的速度为x千米/小时,则小汽车的速度为3x千米/小时,‎ 由题意可列方程为 -2- = ,‎ 解得x=20.‎ 经检验x=20符合题意,‎ 故3x=60.‎ 即公共汽车的速度为20千米/小时,小汽车的速度为60千米/小时.‎ ‎20.解：(1)x1=c,x2=.‎ ‎(2)∵x+ = a + ,‎ ‎∴x-1 + = a-1+ ,‎ 由(1)可得：x-1=a-1或x-1=,‎ ‎∴x1=a,x2=.‎