2020-2021学年初二数学上册单元真题训练：数据的收集与表示 9页

2020-2021 学年初二数学上册单元真题训练：数据的收集与表示 一、选择题（本大题共 12 个小题，每小题 4 分，共 48 分） 1、下列调查中，调查方式选择合理的是（ C ） A、了解某批次汽车的抗撞能力，选择全面调查 B、了解某公园全年的游客流量，选择全面调查 C、某校选出短跑最快的学生参加全市比赛，选择全面调查 D、了解某班学生的身高情况，选择抽样调查 2、某市有 3000 名初一学生参加期末考试，为了了解这些学生的数学成绩，从中抽取 200 名 学生的数学成绩进行统计分析、在这个问题中，下列说法： ①这 3000 名初一学生的数学成绩的全体是总体； ②每个初一学生的数学成绩是个体； ③200 名初一学生的数学成绩是总体的一个样本； 其中说法正确的是（ A ） A、3 个 B、2 个 C、1 个 D、0 个 3、以下问题，不适合采用全面调查方式的是（ D ） A、调查全班同学对“西成”高铁的了解程度 B、“冠状病毒”疫情期间，对所有疑似病例病人进行病毒检测 C、为准备开学，对全班同学进行每日温度测量统计 D、了解西安市全体中小学生对“冠状病毒”的知晓程度 4、下列调查中，调查方式选择合理的是（ A ） A、为了了解北斗三号卫星零件的质量情况，选择全面调查 B、为了了解胜溪湖森林公园全年的游客流量，选择全面调查 C、为了了解某品牌木质地板的甲醛含量，选择全面调查 D、新冠肺炎疫情期间，为了了解出入某小区的居民的体温，选择抽样调查 5、已知一组数据 2 1− ， ， 4− ， 3 21 ， 52 ，则无理数出现的频率是（ B ） A、20% B、40% C、60% D、80% 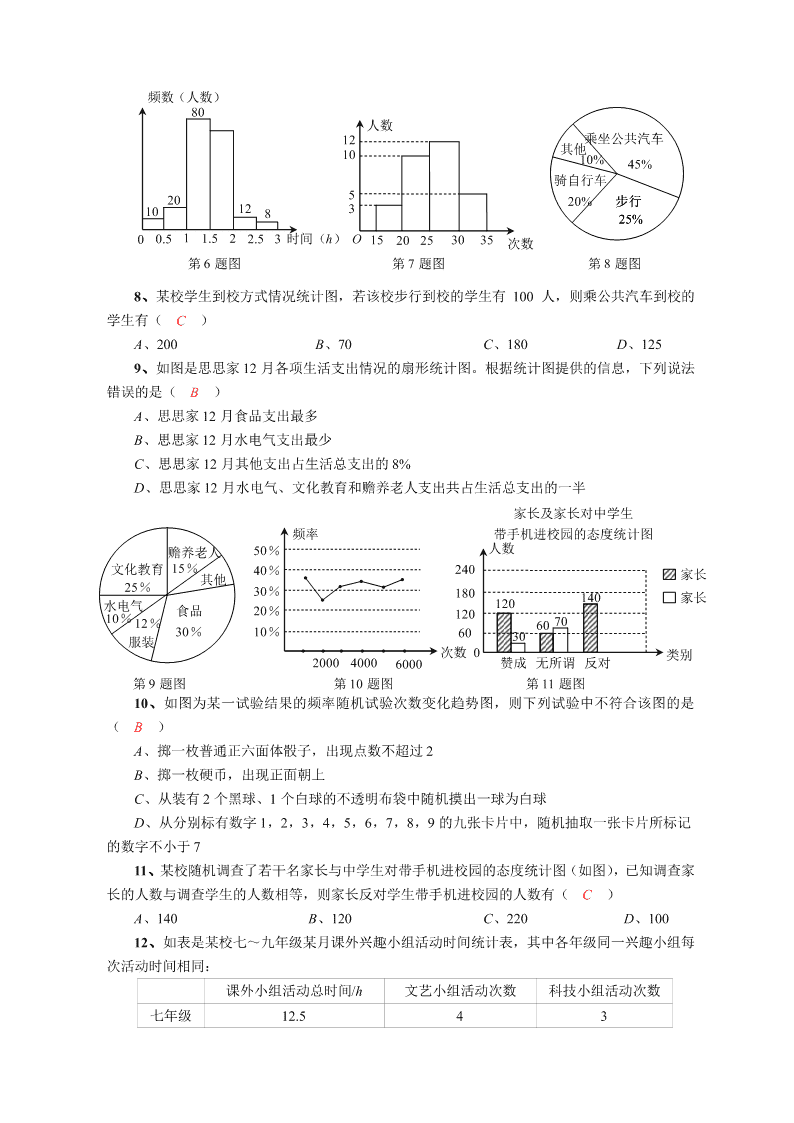6、为提高学生的课外阅读水平，我市各中学开展了“我的梦，中国梦”课外阅读活动，某 校为了解七年级学生每日课外阅读所用的时间情况，从中随机抽取了部分学生，进行了统计分析， 整理并绘制出如图所示的频数分布直方图，有下列说法： ①这次调查属于全面调查 ②这次调查共抽取了 200 名学生 ③这次调查阅读所用时间在 2.5﹣3h 的人数最少 ④这次调查阅读所用时间在 1﹣1.5h 的人数占所调查人数的 40%，其中正确的有（ A ） A、②③④ B、①③④ C、①②④ D、①②③ 7、为了了解本校八年级学生的体能情况，随机抽查了其中 30 名学生，测试了 1 分钟仰卧起 坐的次数，并绘制成如图所示的频数分布直方图，则仰卧起坐次数在 25 次（含 25 次）以上的人 数共有（ C ） A、10 人 B、12 人 C、17 人 D、都不对 第 9 题图 25％ 文化教育 赡养老人 水电气 服装 食品 其他 15％ 10％ 12％ 30％ 频率 次数 50％ 40％ 30％ 20％ 10％ 2000 4000 6000 第 10 题图 人数 类别 240 180 120 60 0 赞成 无所谓 反对 120 30 60 70 140 家长 家长 家长及家长对中学生 带手机进校园的态度统计图 第 11 题图 8、某校学生到校方式情况统计图，若该校步行到校的学生有 100 人，则乘公共汽车到校的 学生有（ C ） A、200 B、70 C、180 D、125 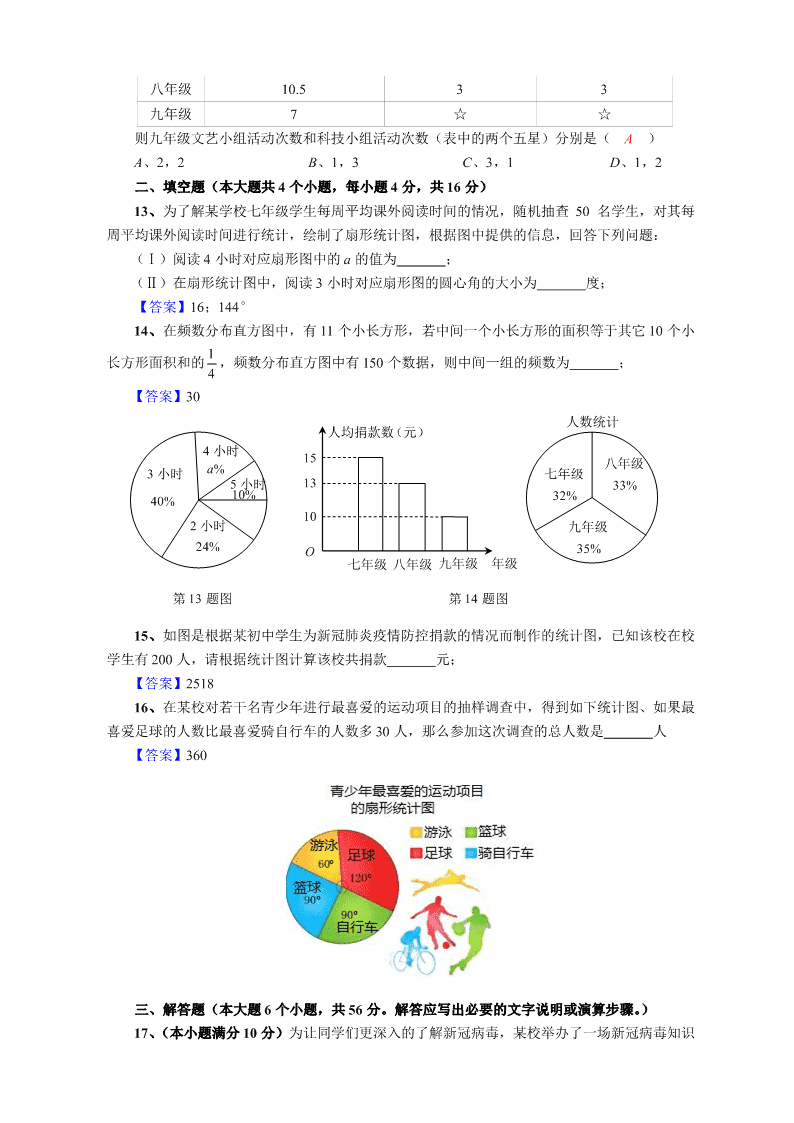9、如图是思思家 12 月各项生活支出情况的扇形统计图。根据统计图提供的信息，下列说法 错误的是（ B ） A、思思家 12 月食品支出最多 B、思思家 12 月水电气支出最少 C、思思家 12 月其他支出占生活总支出的 8% D、思思家 12 月水电气、文化教育和赡养老人支出共占生活总支出的一半 10、如图为某一试验结果的频率随机试验次数变化趋势图，则下列试验中不符合该图的是 （ B ） A、掷一枚普通正六面体骰子，出现点数不超过 2 B、掷一枚硬币，出现正面朝上 C、从装有 2 个黑球、1 个白球的不透明布袋中随机摸出一球为白球 D、从分别标有数字 1，2，3，4，5，6，7，8，9 的九张卡片中，随机抽取一张卡片所标记 的数字不小于 7 11、某校随机调查了若干名家长与中学生对带手机进校园的态度统计图（如图），已知调查家 长的人数与调查学生的人数相等，则家长反对学生带手机进校园的人数有（ C ） A、140 B、120 C、220 D、100 12、如表是某校七～九年级某月课外兴趣小组活动时间统计表，其中各年级同一兴趣小组每 次活动时间相同： 课外小组活动总时间/h 文艺小组活动次数 科技小组活动次数 七年级 12.5 4 3 2.5 0 10 频数（人数） 第 6 题图 20 80 12 8 0.5 1 1.5 2 3 时间（h） 第 7 题图 12 人数 10 5 3 O 15 20 25 30 次数 35 10% 乘坐公共汽车 第 8 题图 45% 25% 步行 其他 20% 骑自行车 25% 步行 人数统计 第 13 题图 3 小时 4 小时 5 小时 2 小时 40% a% 10% 24% 七年级 32% 八年级 33% 九年级 35% 15 人均捐款数（元） 七年级 八年级 九年级 年级 13 10 O 第 14 题图 八年级 10.5 3 3 九年级 7 ☆ ☆ 则九年级文艺小组活动次数和科技小组活动次数（表中的两个五星）分别是（ A ） A、2，2 B、1，3 C、3，1 D、1，2 二、填空题（本大题共 4 个小题，每小题 4 分，共 16 分） 13、为了解某学校七年级学生每周平均课外阅读时间的情况，随机抽查 50 名学生，对其每 周平均课外阅读时间进行统计，绘制了扇形统计图，根据图中提供的信息，回答下列问题： （Ⅰ）阅读 4 小时对应扇形图中的 a 的值为 ； （Ⅱ）在扇形统计图中，阅读 3 小时对应扇形图的圆心角的大小为 度； 【答案】16；144° 14、在频数分布直方图中，有 11 个小长方形，若中间一个小长方形的面积等于其它 10 个小 长方形面积和的 4 1 ，频数分布直方图中有 150 个数据，则中间一组的频数为 ； 【答案】30 15、如图是根据某初中学生为新冠肺炎疫情防控捐款的情况而制作的统计图，已知该校在校 学生有 200 人，请根据统计图计算该校共捐款 元； 【答案】2518 16、在某校对若干名青少年进行最喜爱的运动项目的抽样调查中，得到如下统计图、如果最 喜爱足球的人数比最喜爱骑自行车的人数多 30 人，那么参加这次调查的总人数是 人 【答案】360 三、解答题（本大题 6 个小题，共 56 分。解答应写出必要的文字说明或演算步骤。） 17、（本小题满分 10 分）为让同学们更深入的了解新冠病毒，某校举办了一场新冠病毒知识 学生/人数 成绩/分 1 2 3 4 5 1 1 2 3 4 5 6 7 8 9 10 甲组 乙组 竞赛，满分 10 分，学生得分为整数，成绩达到 6 分以上（包括 6 分）为合格，达到 9 分以上（包 含 9 分）为优秀、这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示。 组别 平均数 中位数 方差 合格率 优秀率 甲组 6.7 3.41 90% 20% 乙组 7.5 70% 10% （1）补充完成上面的成绩统计分析表； （2）小明同学说：“这次竞赛我得了 7 分，在我们小组中排名属中游略偏上!”观察上表可知， 小明是 组的学生；（填“甲”或“乙”） （3）甲组同学说他们组的成绩好于乙组，因为他们组的合格率、优秀率均高于乙组，但乙组 同学不同意，认为他们组的成绩要好于甲组。请你给出两条支持乙组同学观点的理由。 【分析】（1）根据直方图中的数据，可以得到表格中需要填写的数据；（2）根据表格中的数 据，可以得到小明是哪个组的学生；（3）根据表格中的数据，可以写出支持乙组同学的理由。 【解答】解：（1）甲组的中位数是：( ) 6266 =+ 乙组的平均数是： 1.710 1948271625 =++++ ＝7.1 方差是： ( ) ( ) ( ) ( ) ( )  85.11.791.7841.7721.761.7528 1 22222 =−+−+−+−+− 故答案为：6，7.1，1.85， 补全完整的统计表如下图所示， 组别 平均数 中位数 方差 合格率 优秀率 甲组 6.7 6 3.41 90% 20% 乙组 7.1 7.5 1.85 70% 10% （2）∵ 1.776  ∴小明是甲组的学生， 故答案为：甲； （3）支持乙组同学观点的理由是：乙组的平均数高于甲组，乙组的中位数高于甲组，故乙组 的成绩要好于甲组。 【点评】本题考查频数分布直方图、统计表，解答本题的关键是明确题意，利用数形结合的 思想解答。 D B C A 项目 30 20 10 40 50 人数（单位：人） 28％ D B C A 44 8 28 D B C A 项目 30 20 10 40 50 人数（单位：人） 28％ D B C A 20 44 8 28 18、（本小题满分 8 分）全市开展的“体育、艺术 2+1”活动中，某校根据实际情况，决定主 要开设 A：乒乓球，B：篮球，C：跑步，D ：跳绳这四种运动项目、为了解学生喜欢哪一种 项目，随机抽取了部分学生进行调查，并将调查结果绘制成如图甲、乙所示的条形统计图和扇形 统计图、请你结合图中的信息解答下列问题： （1）求本次调查共抽取多少学生？ （2）把条形统计图补充完整； （3）求扇形统计图中 B 所对的圆心角的度数。 【分析】（1）根据条形图和扇形图中给出的 D 的相关数据，计算出抽取的学生数； （2）根据抽取学生数、A、C、D 的人数，先计算出 B 的人数，再补全条形统计图； （3）B 的人数÷抽取人数＝B 占抽取学生的百分比，B 占抽取学生数的百分比×360°＝B 所对圆心角的度数。 【解答】解：（1）调查的人数是： 100%2828 = （人）； （2）喜欢 B 的人数是： 2028844100 =−−− （人）； 补全条形统计图为： （3）B 占调查学生的百分比为： %20100 20 = 所以 B 所对的圆心角为： = 72%20360 答：扇形统计图中 B 所对的圆心角的度数为 72° 【点评】本题考查了条形统计图和扇形统计图，读懂统计图，从不同的统计图中得到必要的 信息是解决问题的关键、条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分 占总体的百分比大小。 19、（本小题满分 8 分）学校为了解疫情期间学生自习课落实“停课不停学，学习不延期” 在线学习的效果，王校长通过网络学习平台，随机抽查了该校部分学生在一节自习课中的学习情 况，发现共有四种学习方式（每人只参与其中一种）：A：阅读电子读物，B：听教师录播课程，C： 完成在线作业，D：线上讨论交流、并根据调查结果绘制成如图两幅不完整的统计图，根据图中 信息，解答下列问题： （1）王校长本次抽查了 名学生； （2）将条形统计图补充完整； （3）求扇形统计图中“C：完成在线作业”对应的圆心角的度数； （4）该校在线学习的学生共有 3200 名，请估计当时全校“B：听教师录播课程”的约有多少 名学生？ 【分析】（1）根据阅读电子读物的人数和所占的百分比求出抽查的总人数； （2）用总人数减去其它学习方式的人数求出线上讨论交流的人数，从而补全统计图； （3）用 360°乘以完成在线作业的人数所占的百分比即可得出答案； （4）用总人数乘以听教师录播课程的学生所占的百分比即可、 【解答】解：（1）王校长本次抽查的学生有： 90%2018 = （名）； 故答案为：90； （2）线上讨论交流的人数有 1224361890 =−−− （人），补全统计图如下： （3）扇形统计图中“完成在线作业”对应的圆心角的度数为 = 9690 24360 ； （4）根据题意得： 128090 363200 = （名） 答：当时全校“B、听教师录播课程”的约有 1280 名学生。 【点评】本题考查的是条形统计图和扇形统计图的综合运用、读懂统计图，从不同的统计图 中得到必要的信息是解决问题的关键。 12 6 0 D B C A 学习方式 30 24 18 36 42 在线学习方式条形统计图 20% D B C A 在线学习方式扇形统计图 18 36 24 12 6 0 D B C A 学习方式 30 24 18 36 42 在线学习方式条形统计图 20% D B C A 在线学习方式扇形统计图 18 36 24 各项报名情况条形统计图 项目 A 70 60 50 40 30 20 10 B 45 15 60 C D 人数 A 40% B C D 20% 各项报名情况扇形统计图 1 O y/人数 x/次数 60 80 2 4 13 18 100 120 140 160 180 20、（本小题满分 8 分）体育委员统计了全班同学 60 秒跳绳的次数，列出了频数分布表和频 数分布直方图、如图： 60≤x＜80 80≤x＜100 80≤x＜120 120≤x＜140 140≤x＜160 160≤x＜180 180≤x＜200 2 a 18 13 8 4 1 （1）频数分布表中 _________=a ；补全频数分布直方图； （2）上表中组距是 ，组数是 组，全班共有 人； （3）跳绳次数在 1 4 01 0 0  x 范围的学生有 人，占全班同学的 %； （4）从图中，我们可以看出怎样的信息？（合理即可） 【分析】（1）根据频数分布直方图中的数据，可以得到 a 的值，然后根据频数分布表中的数 据，可知 1 6 01 4 0  x 这一组的频数，然后即可将频数分布直方图补充完整； （2）根据频数分布表中的数据，可以得到组距和组数，再根据直方图中的数据，可以求出全 班的人数； （3）根据直方图中的数据，可以得到跳绳次数在 范围的学生和占全班的百分比； （4）本题答案不唯一，合理即可。 【解答】解：（1）由直方图中的数据可知， 4=a ，由频数分布表可知， 160140  x 这一组 的频数为 8，补全的频数分布直方图如右图所示，故答案为：4； （2）组距是 2060-80 = ，组数为 7 组，全班共有： 50148131842 =++++++ （人）， 故答案为：20，7，50； （3）跳绳次数在 范围的学生有 311318 =+ （人），占全班同学的 %62%10050 31 = 故答案为：31，62； （4）跳绳次数在 100≤x＜120 范围的同学最多，跳绳次数在 180 以上的人数最少、 【点评】本题考查频数分布直方图、频数分布表，解答本题的关键是明确题意，利用数形结 合的思想解答。 21、（本小题满分 10 分）学校为了解疫情期间学生自习课落实“停课不停学、学习不延期” 在线学习的效果，王校长通过网络学习平台，随机抽查了该校部分学生在一节自习课中的学习情 况，发现共有四种学习方式（每人只参加其中一种）：A、阅读电子教材，B、完成在线作业，C、 线上讨论交流，D、听教师录播课程 垃圾分类知识及投放情况测试成绩条形统计图 优 等级 人数 80 70 60 50 40 30 20 10 良 中 差 72° 良 中 差 优 垃圾分类知识及投放情况测试成绩扇形统计图 请解答以下问题： （1）图 1 中，“完成在线作业”这一项的人数是 ； （2）图 2 中，“线上讨论交流”这一项的百分比是 ，“阅读电子教材”这一项所对应 的扇形的圆心角度数是 ； （3）若该校共有 2200 名学生，请估计该校选择“听教师录播课程”这一项的学生约有多少 人？ 【分析】（1）根据听教师录播课程的人数和所占的百分比求出总人数，再用总人数减去其它 项目的人数，即可求出完成在线作业的人数；（2）用线上讨论交流的人数除以总人数即可得出线 上讨论交流这一项的百分比；用 360°乘以阅读电子教材所占的百分比即可得出答案；（3）用该 校的总人数乘以听教师录播课程所占的百分比即可得出答案、 【解答】解：（1）调查的总学生有： 1 5 0%4060 = （人） “完成在线作业”这一项的人数是： 30601545150 =−−− （人）；故答案为：30； （2）“线上讨论交流”这一项的百分比是： %10%10050 15 = ；“阅读电子教材”这一项所对 应的扇形的圆心角度数是： = 108150 45360 ；故答案为：10%，108°； （3）该校选择“听教师录播课程”这一项的学生约有： 880150 602200 = （人） 【点评】本题考查的是条形统计图和扇形统计图的综合运用、读懂统计图，从不同的统计图 中得到必要的信息是解决问题的关键。 22、（本小题满分 12 分）对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污 染，保护环境、为了调查同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾 分类及投放的相关知识，某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷，并 在本校随机抽取部分同学进行问卷测试，把测试成绩分成“优、良、中、差”四个等级，绘制了 如图不完整的统计图： 根据以上统计信息，解答下列问题： （1）求成绩是“优”的人数占抽取人数的百分比； （2）求本次随机抽取问卷测试的人数； （3）请把条形统计图补充完整； （4）若该校学生人数为 2000 人，请估计成绩是“优”和“良”的学生共有多少人？ 【分析】（1）用成绩是“优”所在扇形圆心角的度数除以 360°即可； （2）用成绩是“优”的人数除以所占的百分比即可； （3）利用总人数减去其它组的人数即可求得成绩是“中”的人数，从而补全条形图； （4）利用总人数 2000 乘以成绩是“优”和“良”的学生所占的百分比即可、 【解答】解：（1）成绩是“优”的人数占抽取人数的百分比是： %20%100360. 72 =  ； （2）本次随机抽取问卷测试的人数是： 200%2040 = （人）； （3）成绩是“中”的人数是 ( ) 60307040200 =++− （人） 条形统计图补充如下： （4） 1100200 70402000 =+ （人） 答：成绩是“优”和“良”的学生共有 1100 人。 【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图 中得到必要的信息是解决问题的关键、条形统计图能清楚地表示出每个项目的数据；扇形统计图 直接反映部分占总体的百分比大小、也考查了利用样本估计总体。 垃圾分类知识及投放情况测试成绩条形统计图 优 等级 人数 80 70 60 50 40 30 20 10 良 中 差 72° 良 中 差 优 垃圾分类知识及投放情况测试成绩扇形统计图