八年级数学上册第十四章整式的乘法与因式分解14-2乘法公式14-2-2完全平方公式教案新版 人教版 3页

‎14．2.2　完全平方公式 ‎1．完全平方公式的推导及其应用．‎ ‎2．完全平方公式的几何解释．‎ 重点 完全平方公式的推导过程、结构特点、几何解释，灵活应用．‎ 难点 理解完全平方公式的结构特征，并能灵活应用公式进行计算．‎ 一、复习引入 你能列出下列代数式吗？‎ ‎(1)两数和的平方；(2)两数差的平方．‎ 你能计算出它们的结果吗？‎ 二、探究新知 你能发现它们的运算形式与结果有什么规律吗？‎ 引导学生用自己的语言叙述所发现的规律，允许学生之间互相补充，教师不急于概括；‎ 举例：(1)(p＋1)2＝(p＋1)(p＋1)＝________________；‎ ‎(2)(p－1)2＝(p－1)(p－1)＝________________；‎ ‎(3)(m＋2)2＝________________；‎ ‎(4)(m－2)2＝________________．‎ 通过几个这样的运算例子，让学生观察算式与结果间的结构特征．‎ 归纳：公式 ‎　　　　　(a＋b)2＝a2＋2ab＋b2‎ ‎　　　　　(a－b)2＝a2－2ab＋b2‎ 语言叙述：两个数的和(或差)的平方，等于它们的平方和，加上(或减去)它们积的2倍．这两个公式叫做(乘法的)完全平方公式．‎ 教师可以在前面的基础上继续鼓励学生发现这个公式的一些特点：如公式左、右边的结构，并尝试说明产生这些特点的原因．‎ 还可以引导学生将(a－b)2的结果用(a＋b)2来解释：‎ ‎(a－b)2＝[a＋(－b)]2＝a2＋2a(－b)＋(－b)2＝a2－2ab＋b2.‎ 三、举例应用 ‎1．教材例3：运用完全平方公式计算：‎ ‎(1)(4m＋n)2；(2)(y－)2.‎ 解：(1)(4m＋n)2＝(4m)2＋2·(4m)·n＋n2‎ ‎＝16m2＋8mn＋n2；‎ ‎(2)(y－)2＝y2－2·y·＋()2‎ ‎＝y2－y＋.‎ 可由学生口答完成，教师多媒体展示结果，提高课堂效率．‎ 3‎ ‎2．教材例4：运用完全平方公式计算：‎ ‎(1)1022＝(100＋2)2＝1002＋2×100×2＋22‎ ‎＝10 000＋400＋4‎ ‎＝10 404；‎ ‎(2)992＝(100－1)2＝1002－2×100×1＋12‎ ‎＝10 000－200＋1‎ ‎＝9 801.‎ 此处可先让学生独立思考，然后自主发言，口述解题思路，可先不给出题目中“运用完全平方公式计算”的要求，允许他们算法的多样化，但要求明白每种算法的局限和优越性．‎ 四、再探新知 ‎1．现有下图所示三种规格的卡片各若干张，请你根据二次三项式a2＋2ab＋b2，选取相应种类和数量的卡片，尝试拼成一个正方形，并讨论该正方形的代数意义：‎ ‎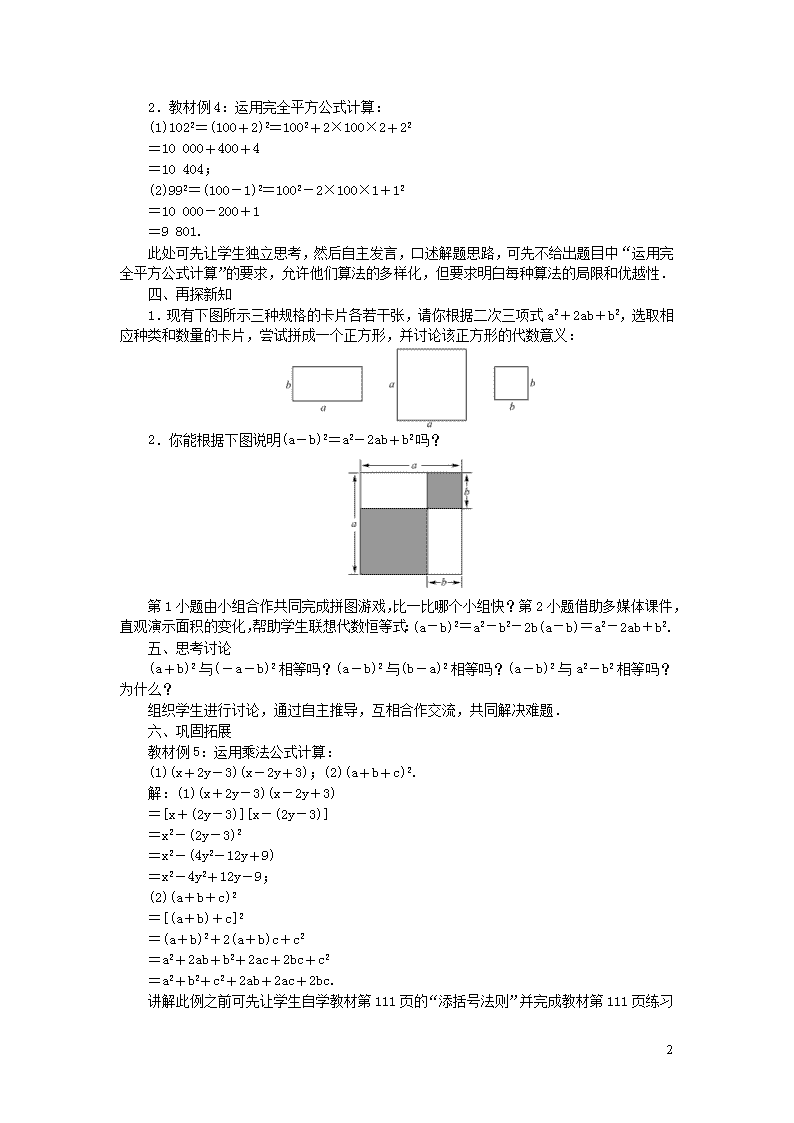2．你能根据下图说明(a－b)2＝a2－2ab＋b2吗？‎ 第1小题由小组合作共同完成拼图游戏，比一比哪个小组快？第2小题借助多媒体课件，直观演示面积的变化，帮助学生联想代数恒等式：(a－b)2＝a2－b2－2b(a－b)＝a2－2ab＋b2.‎ 五、思考讨论 ‎(a＋b)2与(－a－b)2相等吗？(a－b)2与(b－a)2相等吗？(a－b)2与a2－b2相等吗？为什么？‎ 组织学生进行讨论，通过自主推导，互相合作交流，共同解决难题．‎ 六、巩固拓展 教材例5：运用乘法公式计算：‎ ‎(1)(x＋2y－3)(x－2y＋3)；(2)(a＋b＋c)2.‎ 解：(1)(x＋2y－3)(x－2y＋3)‎ ‎＝[x＋(2y－3)][x－(2y－3)]‎ ‎＝x2－(2y－3)2‎ ‎＝x2－(4y2－12y＋9)‎ ‎＝x2－4y2＋12y－9；‎ ‎(2)(a＋b＋c)2‎ ‎＝[(a＋b)＋c]2‎ ‎＝(a＋b)2＋2(a＋b)c＋c2‎ ‎＝a2＋2ab＋b2＋2ac＋2bc＋c2‎ ‎＝a2＋b2＋c2＋2ab＋2ac＋2bc.‎ 3‎ 讲解此例之前可先让学生自学教材第111页的“添括号法则”并完成教材第111页练习第1题．然后给出例5题目，让学生思考选择哪个公式．第(1)小题的解决关键是要引导学生比较两个因式的各项符号，分别找出符号相同及相反的项，学会运用整体思想，将其与公式中的字母a，b对照，其中－2y＋3＝－(2y－3)，故应运用平方差公式．第(2)小题可将任意两项之和看作一个整体，然后运用完全平方公式．‎ 在解此例的过程中，应注意边辩析各项的符号特征，边对照两个公式的结构特征，教师应完整详细地书写解题过程，帮助学生理解这一公式的拓展应用，突破难点．‎ 七、课堂小结 谈一谈：你对完全平方公式有了哪些认识？它与平方差公式有什么区别和联系？‎ 作业：教材第112页习题14.2第2题，第3题的(1)(3)(4)，第4题．‎ 在完全平方公式的探求过程中，学生表现出观察角度的差异：有些学生只是侧重观察某个单独的式子，而不知道将几个式子联系起来看；有些学生则观察入微，表现出了较强的观察力．教师要抓住这个契机，适当对学生进行学法指导．对于公式的特点，则应当左右兼顾，特别是公式的左边，它是正确应用公式的前提．‎ 3‎