2019八年级数学上册 第13章 全等三角形 13互逆命题与互逆定理 2页

互逆命题与互逆定理 教学目标 知识与技能 理解互逆命题与互逆定理，正确应用互逆命题与互逆定理 过程与方法 引导法，演示法，分析法，讨论法 情感态度与价值观 通过创设情境，激发学生的求知欲。通过知识的探索过程，让学生体会成功的喜悦。‎ 教学重点 区分互逆命题与互逆定理 教学难点 区分互逆命题与互逆定理 教学内容与过程 教法学法设计 一. 复习提问，回顾知识，请看下面的问题：‎ 1. 什么是命题？‎ 2. 命题的类型？‎ 3. 命题的组成？‎ 4. 命题的形式？‎ ‎5.把下列命题改写成“如果--------，那么 -------”的形式，并分别指出该命题的题设和结论，并指出命题的类型.‎ ‎1）.同位角相等，两直线平行；‎ ‎2）.全等三角形的对应角相等；‎ ‎3）.直角三角形的两个锐角互余；‎ ‎4）.相等的角是对顶角；‎ ‎5）.锐角的补角是锐角.‎ 二. 导入课题，研究知识：‎ 本节课我们来学习与命题有关的知识---------------互逆命题与互逆定理. ‎ 面向全体学生提出相关的问题。明确要研究，探索的问题是什么，怎样去研究和讨论。.‎ 留给学生一定的思考和回顾知识的时间。‎ 为学生创设表现才华的平台。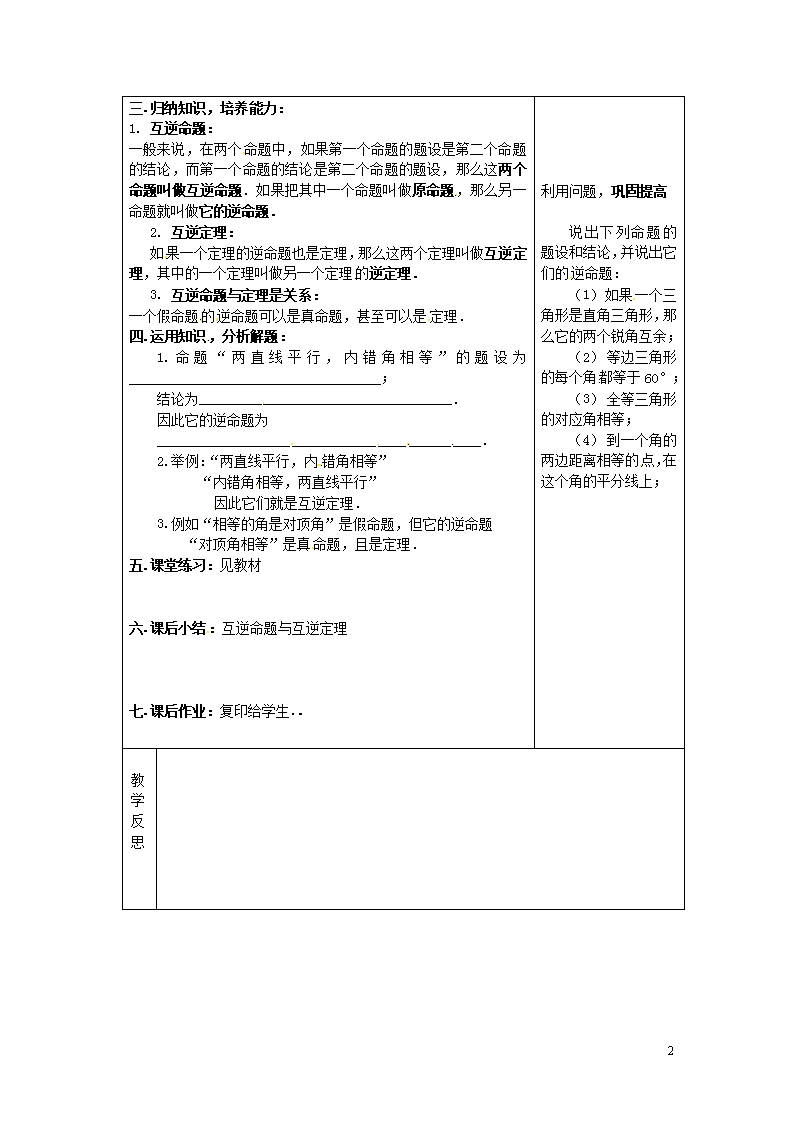‎ 2‎ 三.归纳知识，培养能力：‎ ‎1. 互逆命题：‎ 一般来说，在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题叫做互逆命题．如果把其中一个命题叫做原命题，那么另一命题就叫做它的逆命题．‎ ‎2. 互逆定理：‎ 如果一个定理的逆命题也是定理，那么这两个定理叫做互逆定理，其中的一个定理叫做另一个定理的逆定理．‎ ‎3. 互逆命题与定理是关系：‎ 一个假命题的逆命题可以是真命题，甚至可以是定理．‎ 四.运用知识，分析解题：‎ ‎1.命题“两直线平行，内错角相等”的题设为____________________________________；‎ 结论为____________________________________．‎ 因此它的逆命题为 ‎_____________________________________________．‎ ‎2.举例：“两直线平行，内错角相等”‎ ‎“内错角相等，两直线平行”‎ 因此它们就是互逆定理．‎ ‎3.例如“相等的角是对顶角”是假命题，但它的逆命题 ‎“对顶角相等”是真命题，且是定理．‎ 五.课堂练习：见教材 六.课后小结：互逆命题与互逆定理 七.课后作业：复印给学生..‎ 利用问题，巩固提高 说出下列命题的题设和结论，并说出它们的逆命题：‎ ‎（1） 如果一个三角形是直角三角形，那么它的两个锐角互余；‎ ‎（2） 等边三角形的每个角都等于60°；‎ ‎（3） 全等三角形的对应角相等；‎ ‎（4） 到一个角的两边距离相等的点，在这个角的平分线上；‎ 教学反思 2‎