2010年安徽省芜湖市中考数学试卷 18页

一、选择题（共10小题，每小题4分，满分40分）‎ ‎1、（2010•芜湖）﹣6的绝对值是（　　）‎ ‎ A、﹣6 B、6‎ ‎ C、±6 D、‎‎1‎‎6‎ 考点：绝对值。‎ 分析：绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是是它的相反数；0的绝对值是0．‎ 解答：解：根据负数的绝对值等于它的相反数，得|﹣6|=6．‎ 故选B．‎ 点评：本题考查了绝对值的意义，任何一个数的绝对值一定是非负数．‎ ‎2、（2010•芜湖）2010年芜湖市承接产业转移示范区建设成效明显，一季度完成固定资产投资238亿元，用科学记数法可记作（　　）‎ ‎ A、238×108元 B、23.8×109元 ‎ C、2.38×1010元 D、0.238×1011元 考点：科学记数法—表示较大的数。‎ 专题：应用题。‎ 分析：应先把238亿元整理为用元表示的数，科学记数法的一般形式为：a×10n，在本题中a为2.38，10的指数为整数数位减1．‎ 解答：解：238亿元=23 800 000 000元=2.38×1010元．故选C．‎ 点评：将一个绝对值较大的数写成科学记数法a×10n的形式时，其中1≤|a|＜10，n为比整数位数少1的数．‎ ‎3、（2010•芜湖）一个几何体的三视图如图所示，那么这个几何体是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：由三视图判断几何体。‎ 分析：由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状．‎ 解答：解：由主视图和左视图可得此几何体为柱体，根据俯视图为三角形可得此几何体为三棱柱，故选A．‎ 点评：本题考查由三视图确定几何体的形状，主要考查学生空间想象能力．‎ ‎4、（2010•芜湖）下列命题中是真命题的是（　　）‎ ‎ A、对角线互相垂直且相等的四边形是正方形 B、有两边和一角对应相等的两个三角形全等 ‎ C、两条对角线相等的平行四边形是矩形 D、两边相等的平行四边形是菱形 考点：命题与定理。‎ 分析：分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．‎ 解答：解：A、错误，例如对角线互相垂直的等腰梯形；‎ B、错误，不能确定；‎ C、正确，符合矩形的判定定理；‎ D、错误，两边相等的平行四边形是平行四边形．‎ 故选C．‎ 点评：主要考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．‎ ‎5、（2010•芜湖）要使式子a+2‎a有意义，a的取值范围是（　　）‎ ‎ A、a≠0 B、a＞﹣2且a≠0‎ ‎ C、a＞﹣2或a≠0 D、a≥﹣2且a≠0‎ 考点：二次根式有意义的条件；分式有意义的条件；函数自变量的取值范围。‎ 分析：分子中二次根式的被开方数是非负数，而且分母不能为0，同时满足两个条件，求a的范围．‎ 解答：解：根据题意，得 ‎&a+2≥0‎‎&a≠0‎解得a≥﹣2且a≠0．‎ 故选D．‎ 点评：考查二次根式的意义和性质．概念：式子a（a≥0）叫二次根式．性质：二次根式中的被开方数必须是非负数，否则二次根式无意义．当式子中有分母时还要考虑分母不等于零．‎ ‎6、（2010•芜湖）下列数据：16，20，22，25，24，25的平均数和中位数分别为（　　）‎ ‎ A、21和22 B、22和23‎ ‎ C、22和24 D、21和23‎ 考点：算术平均数；中位数。‎ 专题：计算题。‎ 分析：根据平均数和中位数的概念求解，再判定正确选项．‎ 解答：解：一组数据为16，20，22，25，24，25，‎ ‎∴平均数=（16+20+22+25+24+25）÷6=22；‎ 把数据按从小到大的顺序排列：16，20，22，24，25，25，‎ ‎∴中位数=（22+24）÷2=23．‎ 故选B．‎ 点评：平均数是指在一组数据中所有数据之和再除以数据的个数．找中位数的时候一定要先按大小排好顺序，然后再根据奇数和偶数个来确定中位数．如果数据有奇数个，则正中间的数字即为所求；如果是偶数个，则找中间两位数的平均数．‎ ‎7、（2010•芜湖）关于x的方程（a﹣5）x2﹣4x﹣1=0有实数根，则a满足（　　）‎ ‎ A、a≥1 B、a＞1且a≠5‎ ‎ C、a≥1且a≠5 D、a≠5‎ 考点：根的判别式。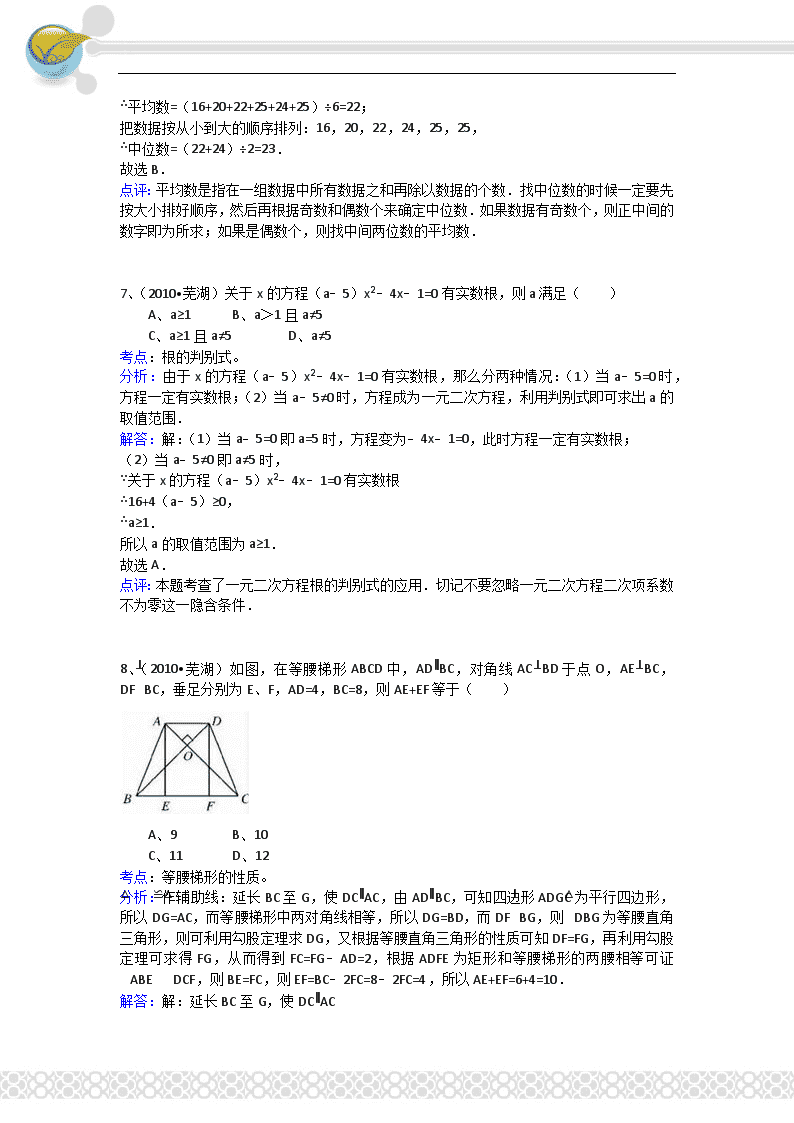‎ 分析：由于x的方程（a﹣5）x2﹣4x﹣1=0有实数根，那么分两种情况：（1）当a﹣5=0时，方程一定有实数根；（2）当a﹣5≠0时，方程成为一元二次方程，利用判别式即可求出a的取值范围．‎ 解答：解：（1）当a﹣5=0即a=5时，方程变为﹣4x﹣1=0，此时方程一定有实数根；‎ ‎（2）当a﹣5≠0即a≠5时，‎ ‎∵关于x的方程（a﹣5）x2﹣4x﹣1=0有实数根 ‎∴16+4（a﹣5）≥0，‎ ‎∴a≥1．‎ 所以a的取值范围为a≥1．‎ 故选A．‎ 点评：本题考查了一元二次方程根的判别式的应用．切记不要忽略一元二次方程二次项系数不为零这一隐含条件．‎ ‎8、（2010•芜湖）如图，在等腰梯形ABCD中，AD∥BC，对角线AC⊥BD于点O，AE⊥BC，DF⊥BC，垂足分别为E、F，AD=4，BC=8，则AE+EF等于（　　）‎ ‎ A、9 B、10‎ ‎ C、11 D、12‎ 考点：等腰梯形的性质。‎ 分析：作辅助线：延长BC至G，使DC∥AC，由AD∥BC，可知四边形ADGC为平行四边形，所以DG=AC，而等腰梯形中两对角线相等，所以DG=BD，而DF⊥BG，则△DBG为等腰直角三角形，则可利用勾股定理求DG，又根据等腰直角三角形的性质可知DF=FG，再利用勾股定理可求得FG，从而得到FC=FG﹣AD=2，根据ADFE为矩形和等腰梯形的两腰相等可证△ABE≌△DCF，则BE=FC，则EF=BC﹣2FC=8﹣2FC=4，所以AE+EF=6+4=10．‎ 解答：解：延长BC至G，使DC∥AC ‎∵AD∥BC ‎∴四边形ADGC为平行四边形 ‎∴DG=AC ‎∵AC⊥BD ‎∴DC⊥BD ‎∵等腰梯形ABCD ‎∴AC=BD ‎∴DG=BD ‎∴△DBG为等腰直角三角形 ‎∴BG2=2BD2∴（BC+AD）2=2BD2∴BD=DG=6‎‎2‎ ‎∵DF⊥BG ‎∴DF=FG ‎∴2DF2=（‎6‎‎2‎）2∴DF=6‎ ‎∴FC=6﹣4=2‎ ‎∵AE⊥BC，DF⊥BC，AD∥BC ‎∴ADFE为矩形 ‎∴AE=DF，AD=EF ‎∵AB=CD，∠AEB=∠DFC ‎∴△ABE≌△DCF ‎∴BE=DF ‎∴EF=BC﹣2FC=8﹣2FC=4‎ ‎∴AE+EF=6+4=10．‎ 故选B．‎ 点评：此题的关键是作辅助线，然后利用等腰梯形的性质和等腰直角三角形求解．‎ ‎9、（2010•芜湖）如图所示，在圆⊙O内有折线OABC，其中OA=8，AB=12，∠A=∠B=60°，则BC的长为（　　）‎ ‎ A、19 B、16‎ ‎ C、18 D、20‎ 考点：垂径定理；等边三角形的性质；等边三角形的判定。‎ 分析：延长AO交BC于D，根据∠A、∠B的度数易证得△ABD是等边三角形，由此可求出 OD、BD的长；过O作BC的垂线，设垂足为E；在Rt△ODE中，根据OD的长及∠ODE的度数易求得DE的长，进而可求出BE的长；由勾股定理知BC=2BE，由此得解．‎ 解答：解：延长AO交BC于D，作OE⊥BC于E；‎ ‎∵∠A=∠B=60°，∴∠ADB=60°；‎ ‎∴△ADB为等边三角形；‎ ‎∴BD=AD=AB=12；‎ ‎∴OD=4，又∵∠ADB=60°，‎ ‎∴DE=‎1‎‎2‎OD=2；‎ ‎∴BE=10；‎ ‎∴BC=2BE=20；‎ 故选D．‎ 点评：此题主要考查了等边三角形的判定和性质以及垂径定理的应用．‎ ‎10、（2010•芜湖）二次函数y=ax2+bx+c的图象如图所示，反比例函数y=ax与正比例函数y=（b+c）x在同一坐标系中的大致图象可能是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：二次函数的图象；正比例函数的图象；反比例函数的图象。‎ 分析：可先根据二次函数的图象与性质判断a、b、c的符号，再判断正比例函数、反比例函数的图象大致位置．‎ 解答：解：由二次函数y=ax2+bx+c的图象开口向上可知a＞0；‎ ‎∵x=﹣b‎2a＞0，‎ ‎∴b＜0；‎ ‎∵图象与y轴交于负半轴，‎ ‎∴c＜0，‎ 即b+c＜0，‎ ‎∴反比例函数y=ax图象在一、三象限，正比例函数y=（b+c）x图象在二、四象限；‎ 故选B．‎ 点评：本题考查正比例函数、反比例函数、二次函数图象与性质．‎ 二、填空题（共6小题，每小题5分，满分30分）‎ ‎11、（2010•芜湖）一个正多边形的每个外角都是36°，这个正多边形的边数是 ．‎ 考点：多边形内角与外角。‎ 分析：多边形的外角和等于360°，因为所给多边形的每个外角均相等，故又可表示成36°n，列方程可求解．‎ 解答：解：设所求正n边形边数为n，‎ 则36°n=360°，‎ 解得n=10．‎ 故正多边形的边数是10．‎ 点评：本题考查根据多边形的外角和求多边形的边数，解答时要会根据公式进行正确运算、变形和数据处理．‎ ‎12、（2010•芜湖）因式分解：9x2﹣y2﹣4y﹣4= ．‎ 考点：因式分解-分组分解法。‎ 分析：此题可用分组分解法进行分解，由于后三项是完全平方式，可以将后三项分为一组．‎ 解答：解：9x2﹣y2﹣4y﹣4，‎ ‎=9x2﹣（y2+4y+4），‎ ‎=9x2﹣（y+2）2，‎ ‎=（3x+y+2）（3x﹣y﹣2）．‎ 点评：本题考查了分组分解法分解因式，用分组分解法进行因式分解的难点是采用两两分组还是三一分组．本题后三项可组成完全平方公式，可把后三项分为一组．‎ ‎13、（2010•芜湖）如图，电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB=1.5m，CD=4.5m，点P到CD的距离为2.7m，则AB与CD间的距离是 m．‎ 考点：相似三角形的应用。‎ 分析：根据AB∥CD，易得，△PAB∽△PCD，根据相似三角形对应高之比等于对应边之比，列出方程求解即可．‎ 解答：解：∵AB∥CD ‎∴△PAB∽△PCD 假设CD到AB距离为X，‎ 则‎2.7﹣X‎2.7‎‎=‎ABCD，‎ 又∵AB=1.5，CD=4.5，‎ ‎∴‎‎2.7﹣X‎2.7‎‎=‎‎1‎‎3‎ ‎∴X=1.8．‎ 点评：此题就主要考查了相似三角形对应高之比等于对应边之比．‎ ‎14、（2010•芜湖）已知x1、x2为方程x2+3x+1=0的两实根，则x13+8x2+20= ．‎ 考点：根与系数的关系；一元二次方程的解。‎ 分析：由于x1、x2是方程的两根，根据根与系数的关系可得到两根之和的值，根据方程解的定义可得到x12、x1的关系，根据上面得到的条件，对所求的代数式进行有针对性的拆分和化简，然后再代值计算．‎ 解答：解：∵x1、x2为方程x2+3x+1=0的两实根，‎ ‎∴x12=﹣3x1﹣1，x1+x2=﹣3；‎ ‎∴x13+8x2+20=（﹣3x1﹣1）x1+8x2+20‎ ‎=﹣3x12﹣x1+8x2+20‎ ‎=﹣3（﹣3x1﹣1）﹣x1+8x2+20‎ ‎=9x1﹣x1+8x2+23‎ ‎=8（x1+x2）+23‎ ‎=﹣24+23‎ ‎=﹣1．‎ 故x13+8x2+20=﹣1．‎ 点评：此题是典型的代数求值问题，涉及到根与系数的关系以及方程解的定义．在解此类题时，如果所求代数式无法化简，应该从已知入手看能得到什么条件，然后根据得到的条件对所求代数式进行有针对性的化简和变形．‎ ‎15、（2010•芜湖）若两圆相切，圆心距是7，其中一圆的半径为10，则另一个圆的半径为 ．‎ 考点：圆与圆的位置关系。‎ 分析：两圆相切，因为圆心距小于一圆的半径，两圆不可能外切，内切时，|10﹣R|=7．‎ 解答：解：因为两圆相切，圆心距为7，设另一个圆的半径为R，‎ 当内切时，|R﹣10|=7，解得R=3或17，‎ 当外切时，|R+10|=7，无解．‎ 点评：本题相切要考虑两种情况，根据两种情况对应的数量关系，分别求解．‎ ‎16、（2010•芜湖）芜湖国际动漫节期间，小明进行了富有创意的形象设计．如图1，他在边长为1的正方形ABCD内作等边三角形BCE，并与正方形的对角线交于F、G点，制成如图2的图标．则图标中阴影部分图形AFEGD的面积= ．‎ 考点：解直角三角形；等边三角形的性质；正方形的性质。‎ 分析：根据等边三角形与正方形的性质，求出∠EBO，再在直角三角形BOF中利用角的正切求出边OF，从而得知S△BOF，S△BAF=S△BAO﹣S△BOF；同理求得S△CGD，所以图标中阴影部分图形AFEGD的面积就是：S□ABCD﹣S△CBE﹣S△BAF﹣S△CGD 解答：解：设AC于BD交与点O，‎ ‎∵AC、BD是正方形的对角线，‎ ‎∴AC⊥BD，OA=OB，‎ 在△BCE中，∠EBC=60°，∠OBC=45°，‎ ‎∴∠EBO=60°﹣45°，‎ ‎∴FO=tan（60°﹣45°）•OB，‎ ‎∴S△BOF=‎1‎‎2‎OF•OB=‎1‎‎2‎tan（60°﹣45°）•OB2，‎ ‎∴S△BAF=S△BAO﹣S△BOF=‎1‎‎2‎OA•OB﹣‎1‎‎2‎tan（60°﹣45°）•OB2=‎1‎‎2‎OB‎2‎﹣‎1‎‎2‎tan（60°﹣45°）•OB2=‎3‎‎﹣1‎‎2‎OB2，‎ 同理，得S△CGD=‎3‎‎﹣1‎‎2‎OB2，‎ ‎∵S△CBE=‎1‎‎2‎CB•BEsin60°=‎1‎‎2‎BC‎2‎sin60°=‎3‎‎4‎AB2，‎ ‎∴S□ABCD﹣S△CBE﹣S△BAF﹣S△CGD=AB2﹣‎3‎‎4‎AB2﹣‎（‎3‎﹣1）‎OB2，‎ ‎∵OB=‎1‎‎2‎BD，BD2=AB2+BD2，AB=BD=1，‎ ‎∴S□ABCD﹣S△CBE﹣S△BAF﹣S△CGD=1﹣‎3‎‎4‎﹣（‎3‎‎﹣1）‎×‎1‎‎4‎×（1+1）=‎3‎‎2‎‎﹣‎‎3‎‎3‎‎4‎，‎ 图标中阴影部分图形AFEGD的面积=‎3‎‎2‎‎﹣‎‎3‎‎3‎‎4‎．‎ 点评：解答本题的难点是求直角三角形ABO中的三角形ABF的面积，在突破难点时，充分利用了等边三角形、正方形的性质以及直角三角形中的边角函数关系．‎ 三、解答题（共8小题，满分80分）‎ ‎17、（2010•芜湖）（1）计算：（1）12010×（‎1‎‎2‎）﹣3+（sin58°﹣π‎2‎）0+|‎3‎﹣4cos600|；‎ ‎（2）求不等式组‎&2x+5＞1‎‎&3x﹣8≤10‎的整数解．‎ 考点：实数的运算；一元一次不等式组的整数解。‎ 分析：（1）本题涉及零指数幂、、负整数指数幂、绝对值乘方、特殊角的三角函数值、二次根式化简六个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果；‎ ‎（2）按照解不等式组的步骤计算．‎ 解答：解：（1）原式=1×8+1+|‎3‎‎﹣2‎|=8+1+2﹣‎3‎=11﹣‎3‎；‎ ‎（2）由①得，x＞﹣2，‎ 由②得，x≤6，‎ ‎∴﹣2＜x≤6．‎ ‎∴满足不等式组的整数解为﹣1、0、1、2、3、4、5、6．‎ 点评：此题主要考查了实数的计算，注意：‎ ‎（1）熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算；‎ ‎（2）注意不等式组解集的确定：大于小，小于大，写在一起错不了．‎ ‎18、（2010•芜湖）图1为已建设封项的16层楼房和其塔吊图，图2为其示意图，吊臂AB与地面EH平行，测得A点到楼顶D点的距离为5m，每层楼高3.5m，AE、BF、CH都垂直于地面，EF=16m，求塔吊的高CH的长？‎ 考点：解直角三角形的应用。‎ 分析：根据AD和每层楼的高度，易求得AE、GH的长，关键是求出CG的值．根据三角形的外角性质，易证得△ABC是等腰△，则BC=AB=EF=16．在Rt△CBG中，已知∠CBG的度数，通过解直角三角形求出CG的长，由此得解．‎ 解答：解：根据题意，得DE=3.5×16=56，AB=EF=16．‎ ‎∵∠ACB=∠CBG﹣∠CAB=15°，‎ ‎∴∠ACB=∠CAB，∴CB=AB=16．‎ ‎∴CG=BC•sin30°=8，‎ CH=CG+HG=CG+DE+AD=8+56+5=69（m）．‎ 故塔吊的高CH为69米．‎ 点评：此题主要考查的是解直角三角形的应用，能够发现△ABC是等腰三角形是解答此题的关键．‎ ‎19、（2010•芜湖）某中学生为调查本校学生平均每天完成作业所用时间的情况，随机调查了50名同学，下图是根据调查所得数据绘制的统计图的一部分．‎ 请根据以上信息，解答下列问题：‎ ‎（1）将统计图补充完整；‎ ‎（2）若该校共有1800名学生，根据以上调查结果估计该校全体学生每天完成作业所用总时间．‎ 考点：加权平均数；用样本估计总体；条形统计图。‎ 专题：图表型。‎ 分析：（1）先求出平均每天完成作业所用时间为4小时的人数，再补全统计图；‎ ‎（2）求出50名学生每天完成作业所用总时间，再算1800名学生每天完成作业所用总时间．‎ 解答：解：（1）正确补全 ‎（2）由图可知x=‎6×1+12×2+16×3+8×4+8×5‎‎6+12+16+8+8‎=3（小时）‎ 可以估计该校全体学生每天完成作业所用总时间=3×1800=5400（小时），‎ 所以该校全体学生每天完成作业所用总时间5400小时．‎ 点评：本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．‎ ‎20、（2010•芜湖）用长度为20m的金属材料制成如图所示的金属框，下部为矩形，上部为等腰直角三角形，其斜边长为2xm．当该金属框围成的图形面积最大时，图形中矩形的相邻两边长各为多少？请求出金属框围成的图形的最大面积．‎ 考点：二次函数的应用。‎ 专题：应用题。‎ 分析：由特殊等腰直角三角形，设出直角边长，再表示其它各边边长，把金属框围成的面积用未知量x表示出来，转化为求函数最值问题，从而求出金属框围成的图形的最大面积．‎ 解答：解：根据题意可得，等腰直角三角形边长为‎2‎xm，矩形的一边长为2xm，‎ 其相邻边长为‎20﹣（4+2‎2‎）x‎2‎=‎10﹣（2+‎2‎）x，‎ ‎∴该金属框围成的面积S=‎2x[10﹣（2+‎2‎）x]+‎1‎‎2‎×‎2‎x•‎2‎x=﹣‎‎（3+2‎2‎）x‎2‎+20x ‎（‎0＜x＜10﹣5‎‎2‎）‎ 当x=‎10‎‎3+2‎‎2‎‎=30﹣20‎‎2‎时，金属围成的面积最大，‎ 此时矩形的一边长2x=‎60﹣40‎‎2‎（m），‎ 相邻边长为10﹣（2+‎2‎）‎•10（3﹣2‎2‎）‎=‎10‎2‎﹣10‎（m），‎ S最大=‎100（3﹣2‎2‎）=300﹣200‎2‎（m‎2‎）‎．‎ 点评：此题考查二次函数的性质及其应用，将实际问题转化为求函数最值问题，从而来解决实际问题，比较简单．‎ ‎21、（2010•芜湖）如图，直角梯形ABCD中，∠ADC=90°，AD∥BC，点E在BC上，点F在AC上，∠DFC=∠AEB．‎ ‎（1）求证：△ADF∽△CAE；‎ ‎（2）当AD=8，DC=6，点E、F分别是BC、AC的中点时，求直角梯形ABCD的面积？‎ 考点：相似三角形的判定与性质；勾股定理；直角梯形。‎ 专题：综合题。‎ 分析：（1）已知∠DFC=∠AEB，则它们的补角也相等；再由梯形的平行线得出的内错角相等，即可判定两个三角形相似．‎ ‎（2）欲求梯形的面积，首先须求出BC的长，那么求出CE的长是解答此题的关键；可在Rt△ACD中，根据勾股定理求出AC的长，进而可求出AF的长；然后根据（1）的相似三角形得出的对应成比例线段，求出EC的长，由此得解．‎ 解答：（1）证明：在梯形ABCD中，AD∥BC，‎ ‎∴∠DAF=∠ACE；‎ ‎∵∠DFC=∠AEB，∴∠DFA=∠AEC；‎ ‎∴△ADF∽△CAE；‎ ‎（2）解：由（1）知：△ADF∽△CAE，∴ADAF=CACE；‎ ‎∵AD=8，DC=6，∠ADC=90°，‎ ‎∴AC=‎8‎‎2‎‎+‎‎6‎‎2‎=10；‎ 又F是AC的中点，∴AF=‎1‎‎2‎AC=5；‎ ‎∴‎8‎‎5‎=‎10‎CD，CE=‎25‎‎4‎；‎ ‎∵E是BC的中点，‎ ‎∴BC=2CE=‎25‎‎2‎；‎ ‎∴直角梯形ABCD的面积=‎1‎‎2‎×（‎25‎‎2‎+8）×6=‎123‎‎2‎．‎ 点评：此题主要考查了直角梯形的性质以及相似三角形的判定和性质．‎ ‎22、（2010•芜湖）“端午”节前，第一次爸爸去超市购买了大小、质量都相同的火腿粽子和豆沙粽子若干，放入不透明的盒中，此时随机取出火腿粽子的概率为‎1‎‎3‎；妈妈发现小亮喜欢吃的火腿粽子偏少，第二次妈妈又去买了同样的5只火腿粽子和1只豆沙粽子放入同一盒中，这时随机取出火腿粽子的概率为‎1‎‎2‎．‎ ‎（1）请计算出第一次爸爸买的火腿粽子和豆沙粽子各有多少只？‎ ‎（2）若妈妈从盒中取出火腿粽子4只、豆沙粽子6只送爷爷和奶奶后，再让小亮从盒中不放回地任取2只，问恰有火腿粽子、豆沙粽子各1只的概率是多少？（用字母和数字表示豆沙粽子和火腿粽子，用列清法计算）‎ 考点：分式方程的应用；概率公式；列表法与树状图法。‎ 分析：（1）等量关系为：原来的火腿粽子数÷原来的总粽子数=‎1‎‎3‎；后来的的火腿粽子数÷后来的总粽子数=‎1‎‎2‎；‎ ‎（2）列举出所有情况，看所求的情况占所有情况的概率如何．‎ 解答：解：（1）设第一次爸爸买了x只火腿粽子，y只豆沙粽子．‎ 则：‎&xx+y=‎‎1‎‎3‎‎&x+5‎x+y+6‎=‎‎1‎‎2‎，‎ 解得：‎&x=4‎‎&y=8‎．‎ 答：第一次爸爸买了4只火腿粽子，8只豆沙粽子．‎ ‎（2）现在有火腿粽子9只，豆沙粽子9只，送给爷爷，奶奶后，还有火腿粽子5只，豆沙粽子3只．‎ 记豆沙粽子a，b，c；火腿粽子1，2，3，4，5．恰好火腿粽子、豆沙粽子各1只的概率为‎30‎‎56‎=‎15‎‎28‎．‎ 点评：解分式方程的关键是找到合适的等量关系；求概率的关键是列举出所有可能的情况．‎ ‎23、（2010•芜湖）如图，BD是⊙O的直径，OA⊥OB，M是劣弧AB上一点，过点M点作⊙O的切线MP交OA的延长线于P点，MD与OA交于N点．‎ ‎（1）求证：PM=PN；‎ ‎（2）若BD=4，PA=‎3‎‎2‎AO，过点B作BC∥MP交⊙O于C点，求BC的长．‎ 考点：切线的性质；垂径定理；相似三角形的判定与性质。‎ 专题：计算题；证明题。‎ 分析：（1）连接OM，MP是圆的切线，OM⊥PM，由角的等量关系可证∠DMP=∠MNP，由此得证．‎ ‎（2）设BC交OM于E，已知直径BD的长，即可得到半径OA、OM的长，根据PA、OA的比例关系，可求出PA、PO的长，通过证△POM∽△OBE，根据相似三角形所得比例线段即可求出BE的长，从而根据垂径定理求出BC的值．‎ 解答：证明：（1）连接OM，‎ ‎∵MP是圆的切线，∴OM⊥PM，‎ ‎∴∠OMD+∠DMP=90°，‎ ‎∵OA⊥OB，‎ ‎∴∠OMP+∠ODM=90°，‎ ‎∵∠MNP=∠OND，∠ODM=∠OMD，‎ ‎∴∠DMP=∠MNP，‎ ‎∴PM=PN．‎ ‎（2）设BC交OM于E，‎ ‎∵BD=4，OA=OB=‎1‎‎2‎BD=2，‎ ‎∴PA=3，‎ ‎∴PO=5；‎ ‎∵BC∥MP，OM⊥MP，‎ ‎∴OM⊥BC，∴BE=‎1‎‎2‎BC；‎ ‎∵∠BOM+∠MOP=90°，在直角三角形OMP中，‎ ‎∠MPO+∠MOP=90°，‎ ‎∴∠BOM=∠MPO；‎ ‎∵∠BEO=∠OMP=90°，‎ ‎∴△OMP∽△BEO，‎ ‎∴OMOP‎=‎BEBO，‎ ‎∴BC=‎8‎‎5‎．‎ 点评：本题主要考查切线的性质和相似三角形的有关知识，题不是很难，做题要细心．‎ ‎24、（2010•芜湖）如图，在平面直角坐标系中放置一矩形ABCO，其顶点为A（0，1）、B（﹣3‎3‎，1）、C（﹣3‎3‎，0）、O（0，0）．将此矩形沿着过E（﹣‎3‎，1）、F（﹣‎4‎‎3‎‎3‎，0）的直线EF向右下方翻折，B、C的对应点分别为B′、C′．‎ ‎（1）求折痕所在直线EF的解析式；‎ ‎（2）一抛物线经过B、E、B′三点，求此二次函数解析式；‎ ‎（3）能否在直线EF上求一点P，使得△PBC周长最小？如能，求出点P的坐标；若不能，说明理由．‎ 考点：二次函数综合题。‎ 专题：压轴题。‎ 分析：（1）根据E、F的坐标，易求出∠EFO的正切值，也就得出了直线EF的斜率，进而可由斜率公式求出直线的EF的解析式；‎ ‎（2）过B′作B′A′⊥BA于A′，在Rt△B′EA′中，通过解直角三角形可求出A′E、A′B′的长，通过证A′E=AE，得出B′在y轴上的结论，从而得出B′坐标，进而用待定系数法求出抛物线的解析式；‎ ‎（3）连接B′C，由于B、B′关于EF所在直线对称，则B′C与折痕的交点即为所求的P点，可求出直线B′C的解析式，联立折痕EF的解析式即可求出P点坐标．‎ 解答：解：（1）由于折痕所在直线EF过E（﹣‎3‎，1）、F（﹣‎4‎‎3‎‎3‎，0），则有：‎ ‎∴tan∠EFO=‎3‎，直线EF的倾斜角为60°；‎ 所以直线EF的解析式为：y﹣1=tan60°•[x﹣（﹣‎3‎）]，‎ 化简得：y=‎3‎x+4．‎ ‎（2）设矩形沿直线EF向右下方翻折后，B、C的对应点为B′（x1，y1），C′（x2，y2）；‎ 过B′作B′A′⊥AE交AE所在直线于A′点；‎ ‎∵B′E=BE=2‎3‎，∠B′EF=∠BEF=60°，‎ ‎∴∠B′EA′=60°，‎ ‎∴A′E=‎3‎，B′A′=3；‎ ‎∴A与A′重合，B′在y轴上；‎ ‎∴x1=0，y1=﹣2，‎ 即B′（0，﹣2）；【此时需说明B′（x1，y1）在y轴上】．‎ 设二次函数解析式为：y=ax2+bx+c，抛物线过B（﹣3‎3‎，1）、E（﹣‎3‎，1）、B′（0，﹣2）；‎ 得到‎&c=﹣2‎‎&3a﹣‎3‎b+c=1‎‎&27a﹣3‎3‎b+c=1‎，‎ 解得‎&a=﹣‎‎1‎‎3‎‎&b=﹣‎‎4‎‎3‎‎3‎‎&c=﹣2‎ ‎∴该二次函数解析式y=﹣‎1‎‎3‎x2﹣‎4‎‎3‎‎3‎x﹣2；‎ ‎（3）能，可以在直线EF上找到P点；‎ 连接B′C交EF于P点，再连接BP；‎ 由于B′P=BP，此时点P与C、B′在一条直线上，故BP+PC=B′P+PC的和最小；‎ 由于BC为定长，所以满足△PBC周长最小；‎ 设直线B′C的解析式为：y=kx+b，则有：‎ ‎&﹣2=b‎&0=﹣3‎3‎k+b‎，‎ 解得‎&k=﹣‎‎2‎‎3‎‎9‎‎&b=﹣2‎；‎ ‎∴直线B′C的解析式为：y=﹣‎2‎‎3‎‎9‎x﹣2；‎ 又∵P为直线B′C和直线EF的交点，‎ ‎∴‎&y=﹣‎2‎‎3‎‎9‎x﹣2‎‎&y=‎3‎x+4‎，‎ 解得‎&x=﹣‎‎18‎‎11‎‎3‎‎&y=﹣‎‎10‎‎11‎；‎ ‎∴点P的坐标为（﹣‎18‎‎3‎‎11‎，﹣‎10‎‎11‎）．‎ 点评：此题主要考查了一次函数、二次函数解析式的确定，轴对称图形的性质、函数图象交点等知识，难度偏大．‎ 参与本试卷答题和审题的老师有：‎ py168；张伟东；kaixinyike；CJX；Linaliu；nhx600；bjy；MMCH；zhangCF；huangling；mmll852；zhangchao；leikun；lanchong；kuaile；lanyuemeng；mama258；智波；lanyan。（排名不分先后）‎ ‎2011年2月17日