重庆市2017年中考数学试题(2) 21页

重庆市2017年初中毕业生学业水平暨普通高中招生考试 数学试题（B卷）‎ 一、选择题：（本大题共12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．‎ ‎1．5的相反数是（ ）‎ A．-5 B．5 C． D．‎ ‎2．下列图形中是轴对称图形的是（ ）‎ A． B． C． D．‎ ‎3．计算结果正确的是（ ）‎ A． B． C． D． ‎ ‎4．下列调查中，最适合采用抽样调查的是（ ）‎ A．对某地区现有的16名百岁以上老人睡眠时间的调查 B．对“神舟十一号”运载火箭发射前零部件质量情况的调查 C．对某校九年级三班学生视力情况的调查 D．对市场上某一品牌电脑使用寿命的调查 ‎5． 估计的值在（ ）‎ A．2到3之间 B．3到4之间 C．4到5之间 D．5到6之间 ‎6．若，则代数式的值为（ ）‎ A．-10 B．-8 C．4 D．10‎ ‎7．若分式有意义，则的取值范围是（ ）‎ A． B． C． D．‎ ‎8．已知，且相似比为，则与的面积比为（ ）‎ A． B． C． D．‎ ‎9．如图，在矩形中，，分别以点为圆心，为半径画弧，交于点 ‎，交于点，则图中阴影部分的面积是（ ）‎ A． B． C． D．‎ ‎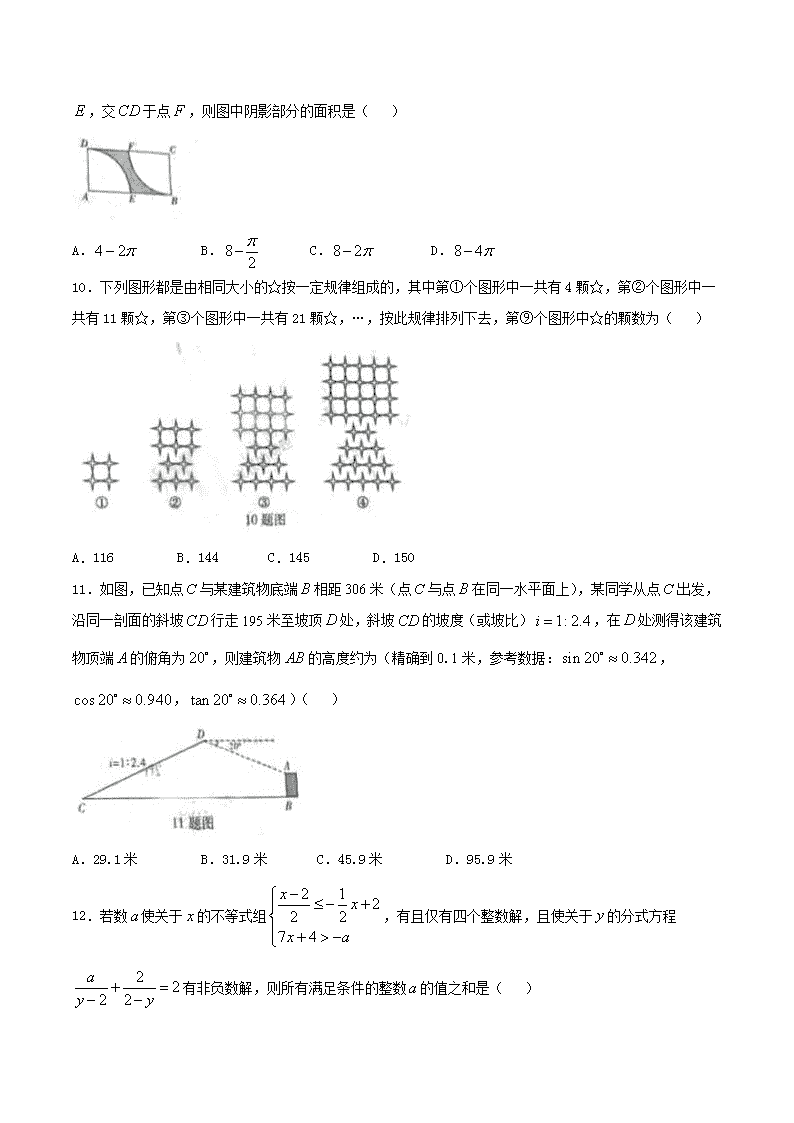10．下列图形都是由相同大小的☆按一定规律组成的，其中第①个图形中一共有4颗☆，第②个图形中一共有11颗☆，第③个图形中一共有21颗☆，…，按此规律排列下去，第⑨个图形中☆的颗数为（ ）‎ A．116 B．144 C．145 D．150‎ ‎11．如图，已知点与某建筑物底端相距306米（点与点在同一水平面上），某同学从点出发，沿同一剖面的斜坡行走195米至坡顶处，斜坡的坡度（或坡比），在处测得该建筑物顶端的俯角为，则建筑物的高度约为（精确到0.1米，参考数据：，，）（ ）‎ A．29.1米 B．31.9米 C．45.9米 D．95.9米 ‎12．若数使关于的不等式组，有且仅有四个整数解，且使关于的分式方程有非负数解，则所有满足条件的整数的值之和是（ ）‎ A．3 B．1 C．0 D．-3‎ 二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上．‎ ‎13．据统计，2017年五一假日三天，重庆市共接待游客约为14 300 000人次，将数14 300 000用科学记数法表示为 ．‎ ‎14．计算： ．‎ ‎15．如图，是的半径，点在上，连接，若，则 度．‎ ‎16．某同学在体育训练中统计了自己五次“1分钟跳绳”的成绩，并绘制了如图所示的拆线统计图，这五次“1分钟跳绳”成绩的中位数是 个．‎ ‎17．甲、乙两人在一条笔直的道路上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，他们分别以不同的速度匀速行驶．已知甲先出发6分钟后，乙才出发，在整个过程中，甲、乙两人的距离（千米）与甲出发的时间（分）之间的关系如图所示，则乙到达终点A时，甲还需_________分钟到达终点B． ‎ ‎18．如图，正方形中，，点是对角线上一点，连接，过点作，交于点，连接，交于点，将沿翻折，得到，连接，交于点，若点是的中点，则的周长是 ．‎ ‎ ‎ 三、解答题：（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上． ‎ ‎19．如图，直线，点在上，交于点，若， ，点在上，求的度数．‎ ‎20．中央电视台的“中国诗词大赛”节目文化品位高，内容丰富．某校初二年级模拟开展“中国诗词大赛”比赛，对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级，并根据成绩绘制成如下两幅不完整的统计图．请结合统计图中的信息，回答下列问题： ‎ ‎（1）扇形统计图中“优秀”所对应扇形的圆心角为_________度，并将条形统计图补充完整；‎ ‎（2）此次比赛有四名同学获得满分，分别是甲、乙、丙、丁．现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛，请用列表法或画树状图法，求出选中的两名同学恰好是甲、丁的概率．‎ 四、解答题：（本大题4个小题，每小题10分，共40分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上． ‎ ‎21．计算：（1）； （2）． ‎ ‎22．如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于A、B两点，与轴交于点，过点作轴于点，点是线段的中点，，，点的坐标为．‎ ‎（1）求该反比例函数和一次函数的解析式；‎ ‎（2）求的面积．‎ ‎23．某地大力发展经济作物，其中果树种植已初具规模，今年受气候、雨水等因素的影响，樱桃较去年有小幅度的减产，而枇杷有所增产．‎ ‎（1）该地某果农今年收获樱桃和枇杷共400千克，其中枇杷的产量不超过樱桃产量的7倍，求该果农今年收获樱桃至少多少千克？‎ ‎（2）该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售，该果农去年樱桃的市场销售量为100千克，销售均价为30元/千克，今年樱桃的市场销售量比去年减少了，销售均价与去年相同，该果农去年枇杷的市场销售量为200千克，销售均价为20元/千克，今年枇杷的市场销售量比去年增加了，但销售均价比去年减少了，该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额与他去年樱桃和枇杷的市场销售总金额相同，求的值．‎ ‎24．如图，中，，，点是上一点，连接．‎ ‎（1）如图1，若，，求的长；‎ ‎（2）如图2，点是线段延长线上一点，过点作于点．连接．当时，求证：．‎ 五、解答题：（本大题2个小题，第25小题10分，第26小题12分，共22分）解答时每小题必须给出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上． ‎ ‎25．对任意一个三位数，如果满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数，把这三个新三位数的和与111的商记为．例如，对调百位与十位上的数字得到213，对调百位与个位上的数字得到321，对调十位与个位上的数字得到132，这三个新三位数的和为，，所以．‎ ‎（1）计算：；‎ ‎（2）若都是“相异数”，其中（都是正整数），规定：，当时，求的最大值．‎ ‎26．如图，在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，对称轴与轴交于点，点在抛物线上．‎ ‎（1）求直线的解析式；‎ ‎（2）点为直线下方抛物线上的一点，连接．当的面积最大时，连接，，点是线段的中点，点是上的一点，点是上的一点，求的最小值；‎ ‎（3）点是线段 的中点，将抛物线沿轴正方向平移得到新抛物线，经过点，的顶点为．在新抛物线的对称轴上，是否存在一点，使得为等腰三角形？若存在，直接写出点的坐标；若不存在，请说明理由．‎