2019九年级数学上册 第二十二章 22二次函数y=ax2+k的图象和性质 2页

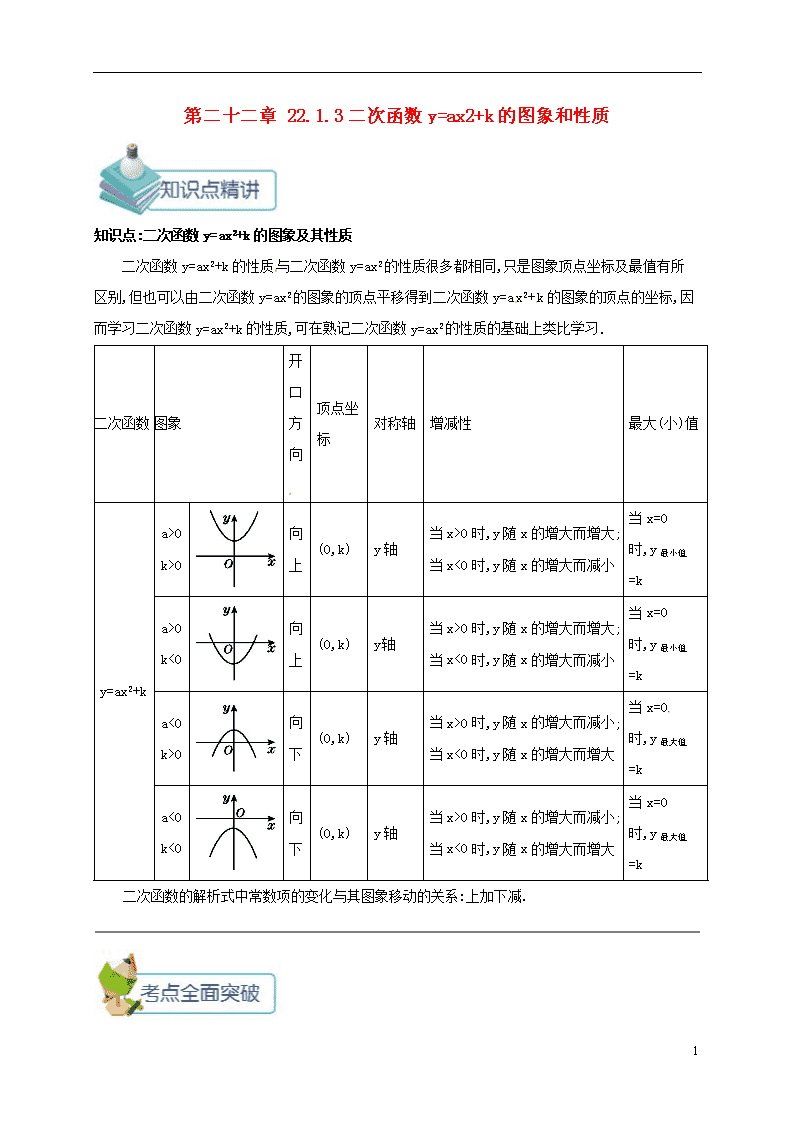
第二十二章 ‎22.1.3‎二次函数y=ax2+k的图象和性质 知识点:二次函数y=ax2+k的图象及其性质 ‎　　二次函数y=ax2+k的性质与二次函数y=ax2的性质很多都相同,只是图象顶点坐标及最值有所区别,但也可以由二次函数y=ax2的图象的顶点平移得到二次函数y=ax2+k的图象的顶点的坐标,因而学习二次函数y=ax2+k的性质,可在熟记二次函数y=ax2的性质的基础上类比学习.‎ 二次函数 图象 开口方向 顶点坐标 对称轴 增减性 最大(小)值 y=ax2+k a>0‎ k>0‎ 向上 ‎(0,k)‎ y轴 当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小 当x=0时,y最小值=k a>0‎ k<0‎ 向上 ‎(0,k)‎ y轴 当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小 当x=0时,y最小值=k a<0‎ k>0‎ 向下 ‎(0,k)‎ y轴 当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大 当x=0时,y最大值=k a<0‎ k<0‎ 向下 ‎(0,k)‎ y轴 当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大 当x=0时,y最大值=k 二次函数的解析式中常数项的变化与其图象移动的关系:上加下减.‎ 2‎ 考点1：二次函数y=ax2+k的图象 ‎【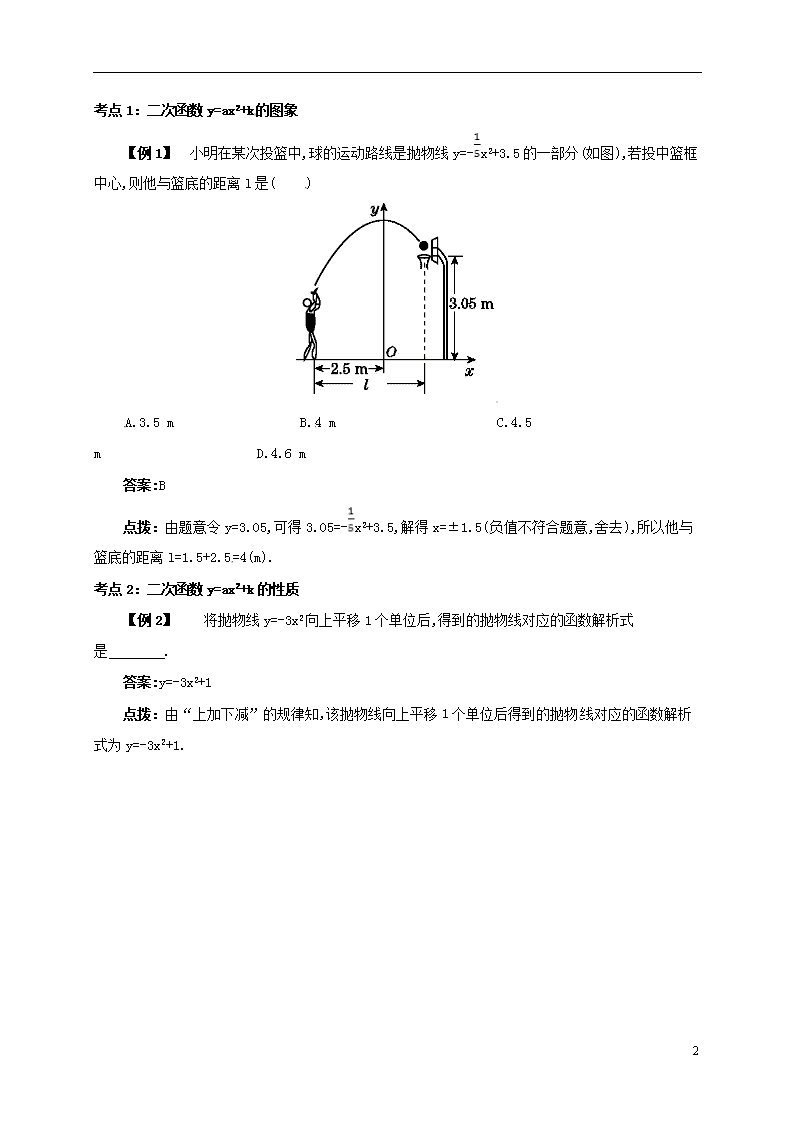例1】　小明在某次投篮中,球的运动路线是抛物线y=-x2+3.5的一部分(如图),若投中篮框中心,则他与篮底的距离l是(　　)‎ A.‎3.5‎ m‎          B.‎4 m            C.‎4.5 m            D.‎‎4.6 m 答案:B　‎ 点拨：由题意令y=3.05,可得3.05=-x2+3.5,解得x=±1.5(负值不符合题意,舍去),所以他与篮底的距离l=1.5+2.5=4(m).‎ 考点2：二次函数y=ax2+k的性质 ‎【例2】  将抛物线y=-3x2向上平移1个单位后,得到的抛物线对应的函数解析式是　　　　. ‎ 答案:y=-3x2+1‎ 点拨：由“上加下减”的规律知,该抛物线向上平移1个单位后得到的抛物线对应的函数解析式为y=-3x2+1.‎ 2‎